オイラーの多面体定理
1 平面グラフのオイラーの定理
$平面上で、線分の長さや線分と線分の角度を考えずに、点と線分のつながりだけに着目した図形を$
$平面グラフといいます。$
$この平面グラフの点、線分、面(線分で囲まれた領域)の個数をそれぞれV(vertex),E(edge),F(face)$
$として、V,E,Fの間に成り立つ関係を求めてみましょう。$
$いくつかの例で、S=V-E+F \ \ の値を求めてみましょう。$
$\hspace{1em} 例1$
 $\quad V=2,\ \ E=1,\ \ F=0 \ \ だから \ \ S=2-1+0=1$
$\quad V=2,\ \ E=1,\ \ F=0 \ \ だから \ \ S=2-1+0=1$
$例2$
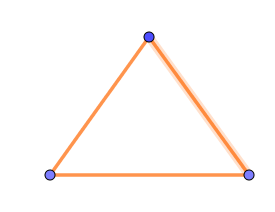
$V=3,\ \ E=3,\ \ F=1 \ \ だから \ \ S=3-3+1=1$
$例3$
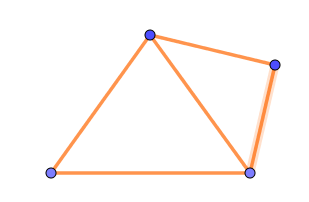
$\quad V=4,\ \ E=5,\ \ F=2 \ \ だから \ \ S=4-5+2=1$
$例4$
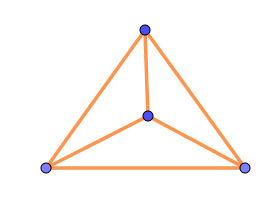
$V=4,\ \ E=6,\ \ F=3 \ \ だから \ \ S=4-6+3=1$
$例5$
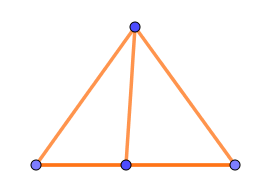
$V=4,\ \ E=5,\ \ F=2 \ \ だから \ \ S=4-5+2=1$
$このように、どのケースでも \ S=1 \ となっていますが、これをFについての数学的帰納法で証明しましょう。$
$(証明)$
$(1)\ \ F=1 のとき (2)で成りたつ。$
$(2)\ \ Fのとき成りたつとすると、F+1 \ には次のような場合がある。$
$\quad V,\ E,\ Fの増分を\Delta V,\ \Delta E,\ \Delta F=1 \ とします。$
(i)$\ 各面の外側に点をとって面を1個増やす場合$
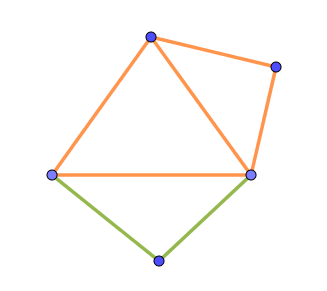
$\Delta V=1,\ \ \Delta E=2,\ \ \Delta F=1 \ \ だから \ \ \Delta S=1-2+1=0$
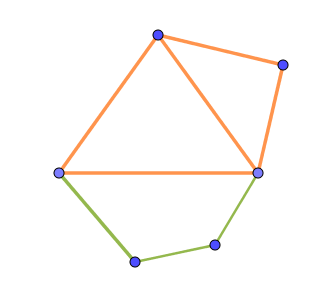
$なお、このとき点を2個とって、\Delta V=2 \ \ としても \ \ \Delta E=3 \ \ だから \ \ \Delta S=2-3+1=0$
$一般に、点をk個とって、\Delta V=k \ \ としても \ \ \Delta E=k+1 \ \ だから \ \ \Delta S=k-(k+1)+1=0$
(ii)$\ 1つの線分上に点をとって面を1つ増やす場合$
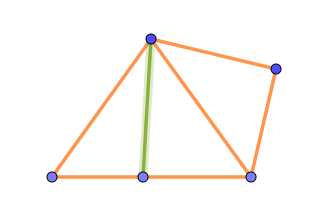
$\Delta V=1,\ \ \Delta E=2,\ \ \Delta F=1 \ \ だから \ \ \Delta S=1-2+1=0$
(iii)$\ 2つの線分上に2点をとって面を1つ増やす場合$
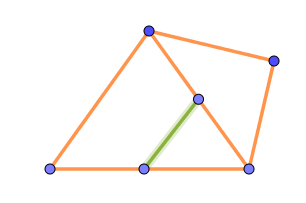
$\Delta V=2,\ \ \Delta E=3,\ \ \Delta F=1 \ \ だから \ \ \Delta S=2-3+1=0$
$このようにSの値の増減は0であるからF+1のときもいえて、常に \ S=1 \ となる。$
$\quad 平面グラフのオイラーの定理$
$\qquad 平面上で、点、線分、面(線分で囲まれた領域)の個数をそれぞれV,\ E,\ F\ とおくと$
$\hspace{5em} V-E+F=1$
2 オイラーの多面体定理
$へこみのない多面体を凸多面体といいますが、ここでは多面体といえば凸多面体のこととします。$
$多面体の点、線分、面(線分で囲まれた領域)の個数をそれぞれV,E,Fとおく。$
$V,E,Fの間に成りたつ関係を求めてみましょう。$
$例$
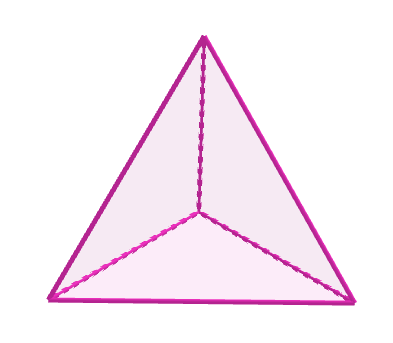
$左図の四面体では、V=4,\ \ E=6,\ \ F=4 \ \ だから \ \ S=4-6+4=2$
$このように、多面体では \ S=2\ となります。$
$\quad オイラーの多面体定理$
$\qquad 凸多面体の頂点、辺、面の個数をそれぞれV,\ E,\ F\ とすると$
$\hspace{5em} V-E+F=2$
$凸多面体からある面の頂点と辺は残したまま、これを取り去ると穴が空いた状態になる。$
$この穴はゴムのように自由に伸び縮みすると考えて、残りの部分を押しつぶす。$
$このとき辺と辺は重ならないように広げてつぶすと平面グラフができる。$
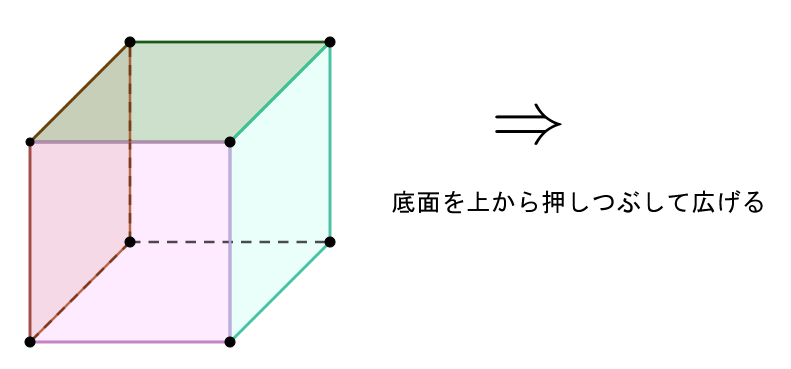
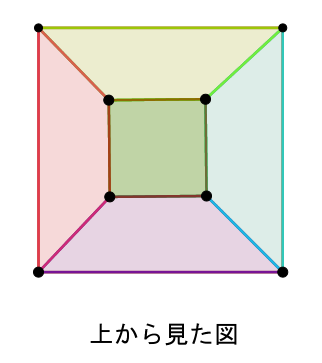
$平面グラフの定理から V-E+F=1$
$凸多面体平には、はじめに取り去った面が1つあるからFに1を加えて \ \ V-E+F=2$
$オイラーの多面体定理を用いる問題を考えましょう。$
$例1 \ \ 右図は一つの頂点に正方形と正三角形が2個ずつ集まってできる多面体です。$
$\qquad 頂点、辺、面の個数を求めましょう。$
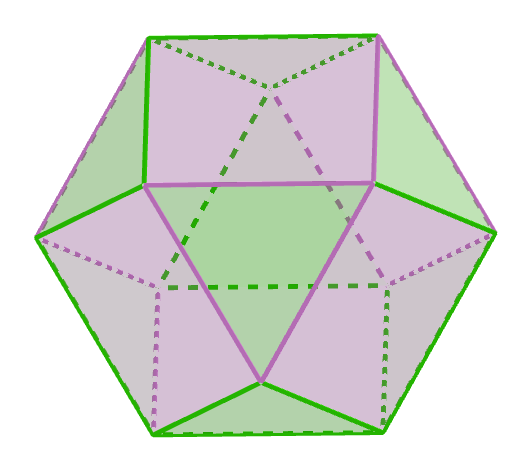
$正方形がx個、正三角形がy個とすると$
(i)$\ 頂点の個数は$
$\quad 正方形で数えると、1つの頂点を2個の正方形が占めているから V=\cfrac{4x}{2}=2x$
$\quad 正三角形で数えると、1つの頂点を2個の正三角形が占めているから V=\cfrac{3y}{2}$
$\quad よって 2x=\cfrac{3y}{2} \quad \therefore y=\cfrac{4}{3}x$
(ii)$\ 辺の個数は \quad 正方形で数えると、E=4x$
(iii)$\ 面の個数は F=x+y=x+\cfrac{4}{3}x=\cfrac{7}{3}x$
$オイラーの多面体定理 V-E+F=2 \ \ に代入して$
$\qquad 2x-4x+\cfrac{7}{3}x=2 \quad \therefore x=6$
$したがって y=8,\ \ V=12,\ \ E=24,\ \ F=14$
$この立体は、立方体の各辺の中点を結んでできる多面体で、$立方八面体$という準正多面体です。$
$次の条件を満たす凸多面体を$準正多面体$といいます。$
$\quad (1) \ 各面は2種類以上の正多角形である。$
$\quad (2)\ 各頂点に集まる面の種類と数はすべて等しい。$
$例2 \ \ 右図は、1つの頂点に正五角形が3個集まってできる多面体です。$
$\qquad 頂点、辺、面の個数を求めましょう。$
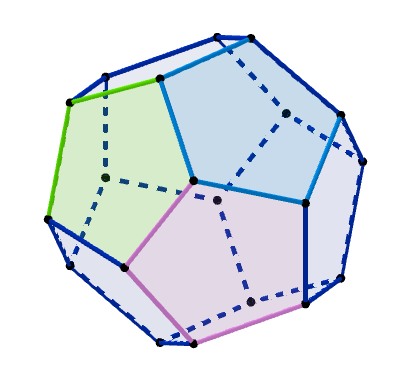
$頂点の個数は、1つの頂点を3つの五角形が占めているから \ \ V=\cfrac{5F}{3}$
$辺の個数は、1つの辺を2つの五角形が占めているから \ \ E=\cfrac{5F}{2}$
$オイラーの多面体定理 V-E+F=2 に代入して$
$\qquad \cfrac{5F}{3}-\cfrac{5F}{2}+F=2 \quad \therefore F=12$
$したがって V=20,\ \ E=30$
$この多面体を$正十二面体$といいます。正多面体については$ (正多面体$を参照してください)$
$例3\ \ 右図は、1つの頂点に正方形1個と正六角形が2個集まってできる準正多面体です。$
$\qquad 頂点、辺、面の個数を求めましょう。$

$正方形がx個、正六角形がy個とすると$
(i)$\ 頂点の個数は$
$\quad 正方形で数えると、1つの頂点を1個の正方形が占めているから V=4x$
$\quad 正三角形で数えると、1つの頂点を2個の正六角形が占めているから V=\cfrac{6y}{2}=3y$
$よって 4x=3y \quad \therefore y=\cfrac{4}{3}x$
(ii)$\ 辺の個数は、1つの辺を正方形と正六角形、あるいは2個の正六角形が占めているから$
$\qquad E=\cfrac{4x+6y}{2}=\cfrac{4x+8x}{2}=6x$
(iii)$\ 面の個数は F=x+y=x+\cfrac{4}{3}x=\cfrac{7}{3}x$
$オイラーの多面体定理 V-E+F=2 \ \ に代入して$
$\qquad 4x-6x+\cfrac{7}{3}x=2 \quad \therefore x=6$
$したがって y=8,\ \ V=24,\ \ E=36,\ \ F=14$
$この立体は、正八面体の各辺の3等分点を結んでできる準正多面体で、$切頂八面体$とよばれています。$
メインメニュー に戻る