MY MATH NOTE

正多面体

　
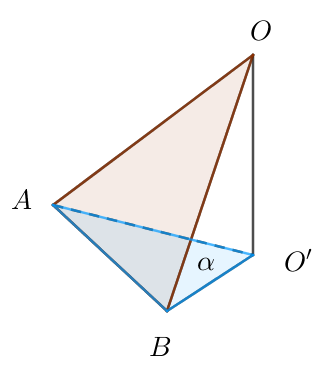
$点Oを頂点とする1つの多角形のOを挟む2辺上に点A、Bをとり、\bigtriangleup OAB \ を考える。$
$頂点Oより、線分ABを含む \bigtriangleup OAB \ 以外の平面\alpha を考え、この平面\alphaに垂線を下ろし$
$OO'とする。すなわち \ \ OO' \perp \alpha $

$OO' \perp \alpha \ \ より　OO' \perp \bigtriangleup O'AB \quad \therefore OO' \perp AO'$
$よって、OA は直角三角形OAO' の斜辺だから　OA > O'A$
$同様にして、OB > O'B$

$△O'AB を辺ABを軸にして \bigtriangleup OABに重なるように(同一平面上くるように)回転させる。$
$(あるいは、2つの三角形を同一平面上に辺ABが重なるようにおくでもよい。)$

　
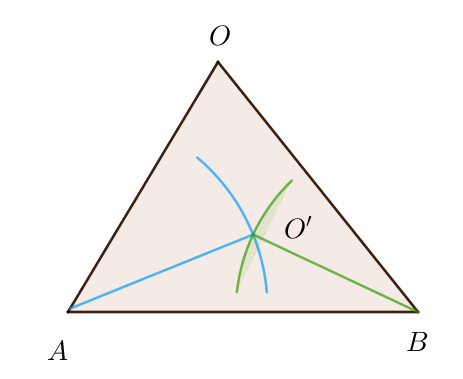
$このとき$
$点Aを中心として半径AO'の円を、さらに、点Bを中心として半径BO'の円をかくと$
$交点O'は \bigtriangleup OABの内部にある。$


$AO'の延長と辺ABとの交点をDとすると$

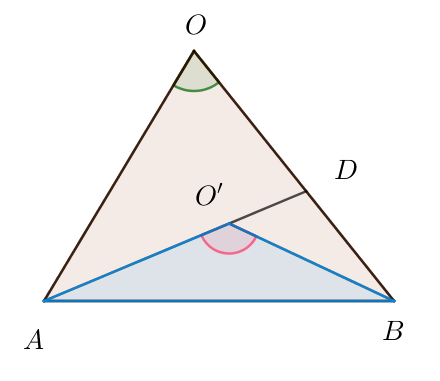　 $\qquad \angle AOD < \angle AOD + \angle OAD = \angle ADB < \angle O'DB + \angle O'BD = \angle AO'B$
$よって$
$\qquad \angle AOB < \angle AO'B$




$一般に　１つの頂点に集まるn個の多角形の角の和は$

　
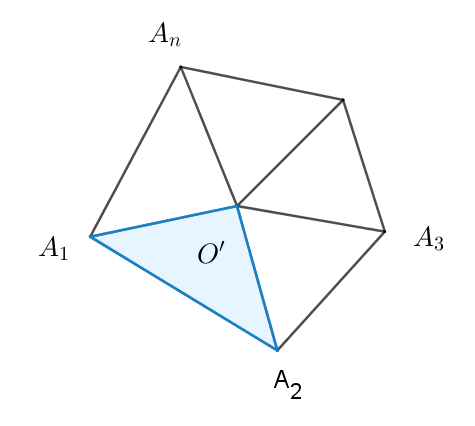
$\hspace{3em} \angle A_1OA_2 + \angle A_2OA_3 + \cdots + \angle A_nOA_1 $
\begin{eqnarray*} &<& \angle A_1O'A_2 + \angle A_2O'A_3 + \cdots + \angle A_nO'A_1 \\ \\ &=&360 °\\ \end{eqnarray*}

$次の条件を満たす凸多面体を$正多面体$といいます。$
$\quad (1)\ 各面はすべて合同な正多角形である。$
$\quad (2)\ 各頂点に集まる面の数はすべて等しい。$

$定理 \quad 正多面体は5種類ある。$

　
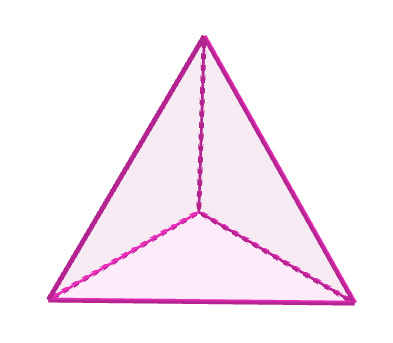
$\quad V=\cfrac{3F}{3}=F,\quad E=\cfrac{3F}{2}$
$オイラーの多面体定理 \ \ V-E+F=2 \ \ に代入して$
$\quad F-\cfrac{3F}{2}+F=2 \ \ より \ \ F=4$
$したがって、　V=4,\quad E=6$

$これは、$正四面体$である。$


(ii)$\ 4個のとき$

　
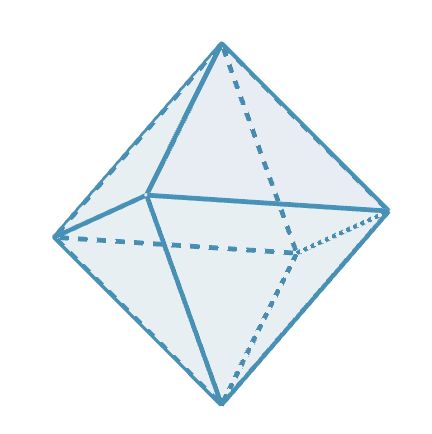
$\quad V=\cfrac{3F}{4},\quad E=\cfrac{3F}{2}$
$\quad \cfrac{3F}{4}-\cfrac{3F}{2}+F=2 \ \ より \ \ F=8$
$したがって、　V=6,\quad E=12$

$これは、$正八面体$である。$


(iii)$\ 5個のとき$

　
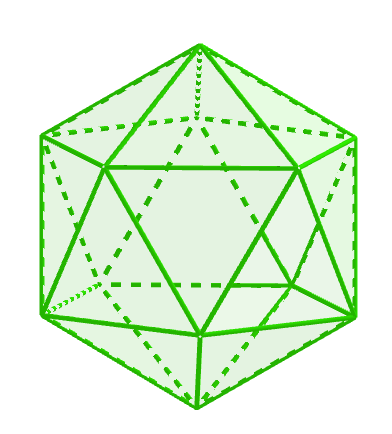
$\quad V=\cfrac{3F}{5},\quad E=\cfrac{3F}{2}$
$\quad \cfrac{3F}{5}-\cfrac{3F}{2}+F=2 \ \ より \ \ F=20$
$したがって、　V=12,\quad E=30$

$これは、$正二十面体$である。$


$1つの頂点に集まる面の数が6個以上のときは、角の大きさの和は360°以上となる。$


$(2)\ 正方形のとき$

$1つの頂点に集まる面の数が3個のとき$

　
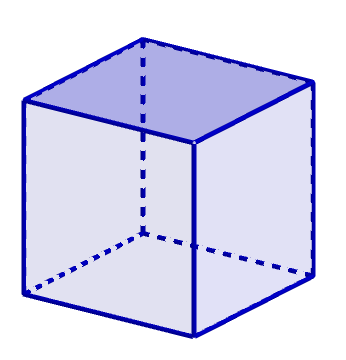
$\quad V=\cfrac{4F}{3},\quad E=\cfrac{4F}{2}=2F$
$オイラーの多面体定理 \ \ V-E+F=2 \ \ に代入して$
$\quad \cfrac{4F}{3}-2F+F=2 \ \ より \ \ F=6$
$したがって、　V=8,\quad E=12$

$これは、$立方体$である。$


$1つの頂点に集まる面の数が4個以上のときは、角の大きさの和は360°以上となる。$


$(2)\ 正五角形のとき$

$1つの頂点に集まる面の数が3個のとき$

　
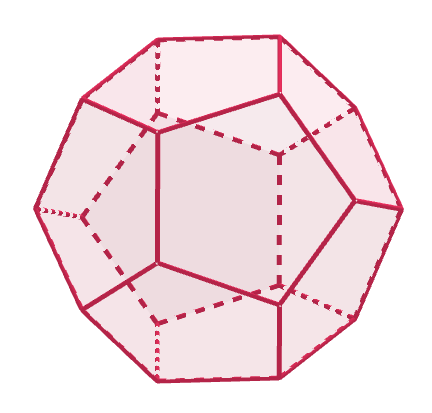
$\quad V=\cfrac{5F}{3},\quad E=\cfrac{5F}{2}$
$オイラーの多面体定理 \ \ V-E+F=2 \ \ に代入して$
$\quad \cfrac{5F}{3}-\cfrac{5F}{2}+F=2 \ \ より \ \ F=12$
$したがって、　V=20,\quad E=30$

$これは、$正十二面体$である。$


$1つの頂点に集まる面の数が4個以上のときは、角の大きさの和は360°以上となる。$


$以上より、正多面体はこれらの5種類である。$



　

ページの先頭へ↑