MY MATH NOTE

同志社大学(理系) 2024年　問題Ⅲ

$p\ を実数とする。座標平面上の点 \ P(4p,\ -\sqrt{18p^2+2})\ と放物線 \ C: y=\cfrac{3}{8}x^2 \ \ を考える。\alpha < \beta \ \ である$
$実数 \ \alpha ,\ \beta \ \ について、放物線 \ C\ 上の \ 2\ 点 \ L(\alpha,\ \cfrac{3}{8}\alpha ^2),\ \ M(\beta,\ \cfrac{3}{8}\beta ^2)\ \ における \ C\ の接線をそれぞれ \ \ell,\ \ m$
$としたとき、\ell \ と \ m\ はともに点 \ P\ を通るとする。原点 \ O\ から直線 \ LM\ に下ろした垂線を \ OH\ とする。$
$次の問いに答えよ。$
$(1)\ \ 実数 \ s\ に対して、C\ 上の点(s,\ \cfrac{3}{8}s ^2)\ における \ C\ の接線を考える。この接線の傾きおよび \ y\ 切片を$
$\quad それぞれ \ s\ を用いて表せ。$
$(2)\ \ \alpha + \beta ,\ \ \alpha \beta \ \ を \ p\ の式で表せ。$
$(3)\ \ 直線 \ LM\ の傾きおよび \ y\ 切片をそれぞれ \ p\ を用いて表せ。また、線分 \ OH\ の長さを求めよ。$
$(4)\ \ p\ が \ \ -\cfrac{1}{3} \leqq p \leqq \cfrac{1}{3} \ \ の範囲を動くとき、点 \ H\ の軌跡の長さを求めよ。$
$(5)\ \ p\ が(4)の範囲を動くとき、線分 \ HM\ が通過する領域の面積を求めよ。$

(1)

(2)

(3)

　
$2\ 点 \ L(\alpha,\ \cfrac{3}{8}\alpha ^2),\ \ M(\beta,\ \cfrac{3}{8}\beta ^2)\ \ を通る直線は$

$傾き=\cfrac{\dfrac{3}{8}\alpha ^2-\dfrac{3}{8}\beta ^2}{\alpha - \beta}=\cfrac{3}{8} \cdot \cfrac{\alpha ^2-\beta ^2}{\alpha - \beta}=\cfrac{3}{8} (\alpha + \beta)=\cfrac{3}{8} \times 8p=3p$

$よって方程式は$
\begin{eqnarray*} y &=&\cfrac{3}{8} (\alpha + \beta)(x-\alpha)+\cfrac{3}{8}\alpha ^2\\ \\ &=&\cfrac{3}{8}(\alpha + \beta)x-\cfrac{3}{8} (\alpha + \beta)\alpha +\cfrac{3}{8}\alpha ^2\\ \\ &=&\cfrac{3}{8}(\alpha + \beta)x-\cfrac{3}{8} \alpha \beta\\ \end{eqnarray*}
$y切片は \quad -\cfrac{3}{8} \alpha \beta=-\cfrac{3}{8} \times \big(-\cfrac{8}{3}\sqrt{18p^2+2}\big)=\sqrt{18p^2+2}$


$(補充)$

$直線LM をこの放物線Cの極線、交点Pを極といいますが、2次曲線の極と極線については$2次曲線の極と極線$を参考にしてください。$


$したがって \quad LM :y=3px + \sqrt{18p^2+2} \quad だから$

$3px-y + \sqrt{18p^2+2}=0$

$OH=\cfrac{\sqrt{18p^2+2}}{\sqrt{(3p)^2+(-1)^2}}=\cfrac{\sqrt{2(9p^2+1)}}{\sqrt{9p^2+1}}=\sqrt{2}$

$なお、この求め方については$点と直線の距離$を参考にしてください。$

$しかし、この求め方では次の(4)が求められない。$


$(OHを求める別解)$

$直線 \ LM\ の傾きが \ 3p\ だからこれと垂直な直線の傾きは \ \ -\cfrac{1}{3p}$

$よって 直線 \ OH\ は \quad y=-\cfrac{1}{3p}x$

$直線 \ LM \ と直線 \ OH\ の共有点は$
\[ \hspace{1em} \left\{ \begin{array}{l} y=3px + \sqrt{18p^2+2} \\ y=-\cfrac{1}{3p}x\\ \end{array} \right. \]
$3px + \sqrt{18p^2+2}=-\cfrac{1}{3p}x$

$\big(3p + \cfrac{1}{3p}\big)x= -\sqrt{18p^2+2}$

$\cfrac{9p^2+1}{3p}x= -\sqrt{18p^2+2}$

$x=\cfrac{3p}{9p^2+1} \times \big( -\sqrt{18p^2+2}\big)=-3p \times \cfrac{\sqrt{2(9p^2+1)}}{9p^2+1}=-\cfrac{3\sqrt{2}p}{\sqrt{9p^2+1}}$

$y=-\cfrac{1}{3p} \times \big(-\cfrac{3\sqrt{2}p}{\sqrt{9p^2+}1}\big)=\cfrac{\sqrt{2}}{\sqrt{9p^2+1}}$

$したがって \quad H(-\cfrac{3\sqrt{2}p}{\sqrt{9p^2+1}},\ \cfrac{\sqrt{2}}{\sqrt{9p^2+1}})$

$OH^2=\cfrac{18p^2}{9p^2+1} + \cfrac{2}{9p^2+1}=\cfrac{18p^2+2}{9p^2+1}=2$

(4)

　
$(3)より \ H(-\cfrac{3\sqrt{2}p}{\sqrt{9p^2+1}},\cfrac{\sqrt{2}}{\sqrt{9p^2+1}}) \quad だから$

$x=-\cfrac{3\sqrt{2}p}{\sqrt{9p^2+1}},\quad y=\cfrac{\sqrt{2}}{\sqrt{9p^2+1}} \quad とおくと$

$x^2+y^2=\cfrac{18p^2}{9p^2+1}+\cfrac{2}{9p^2+1}=\cfrac{18p^2+2}{9p^2+1}=2$

$よって \ 点 \ H\ は、原点中心、半径 \ \sqrt{2}\ の円周上の点である。$

$-\cfrac{1}{3} \leqq p \leqq \cfrac{1}{3} \ \ より \quad p^2 \leqq \cfrac{1}{9}$

$\sqrt{9p^2+1} \leqq \sqrt{2} \qquad \cfrac{1}{\sqrt{9p^2+1}} \geqq \cfrac{1}{\sqrt{2}}$

$\therefore \ \ y=\cfrac{\sqrt{2}}{\sqrt{9p^2+1}} \geqq 1$

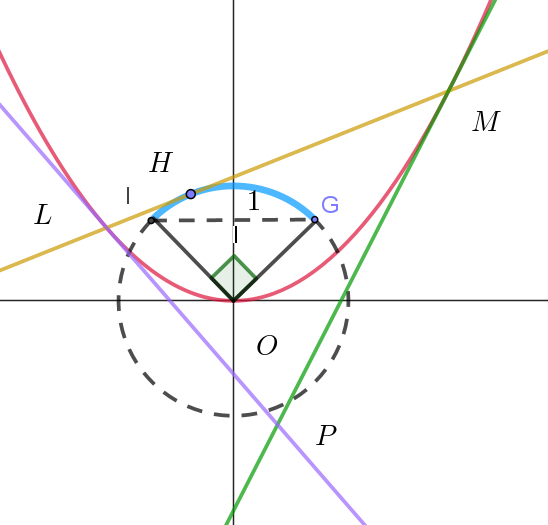
$y=1\ である円周上の \ 2\ 点は、G(1,\ 1),\ \ I(-1,\ 1)\ \ だから、\angle GOI=90°$

$よって \ 点 \ H\ の軌跡は右図のとおりで、半径 \ \sqrt{2}\ の円周の \ \cfrac{1}{4}\ であるから$

$その長さは \quad 2\pi \times \sqrt{2} \times \cfrac{1}{4}=\cfrac{\sqrt{2}}{2}\pi$

(5)

　
$はじめに、線分 \ HM\ が通過する領域を求める。$

$原点 \ O\ から直線 \ LM\ に下ろした垂線が \ OH\ だから \ \ OH \perp HM$

$(4)より点 \ H\ は原点中心、半径 \ \sqrt{2}\ の円周上の点である。$

$したがって、H\ におけるこの円の接線が \ HM\ で、$

$この接線と放物線Cの交点が点 \ M\ である。$

$P=-\cfrac{1}{3}\ \ のときの点 \ H\ を \ A\ とすると \ \ A((1,\ 1)、$

$点 \ A\ における接線と放物線 \ C\ との交点 \ M\ を \ F\ とおく。$

$P=\cfrac{1}{3} \ \ のときの点 \ H\ を \ B\ とすると \ \ B((-1,\ 1)、点 \ B\ に接線と放物線 \ C\ との交点 \ M\ を \ G\ とおく。$

$p\ が \ \ -\cfrac{1}{3} \leqq p \leqq \cfrac{1}{3} \ \ の範囲を動くとき、点 \ H\ は円周上を \ A\ から \ B まで動き、それにともなって点 \ M\ は$

$放物線 \ C\ 上を点 \ F\ から点 \ G\ まで動くから、線分 \ HM\ が通過する領域は右図の青色のついた部分である。$

　
$次に、線分 \ HM\ が通過する領域の面積を求める。$

$円 \ \ x^2+y^2=2\ \ 上の点(x_0,\ y_0)\ \ における接線は$

$ x_0x+y_0y=2 \ \ であるから$

$A(1,\ 1)\ における接線は \quad x+y=2$

$これと放物線Cとの交点は \quad \cfrac{3}{8}x^2=-x+2 \ \ を解いて$

$x=\cfrac{4}{3} \qquad よって \quad F(\cfrac{4}{3},\ \cfrac{2}{3})$

$B(-1,\ 1)\ における接線は \quad -x+y=2$

$これと直線 \ x=1\ との交点は \ \ E(1,\ 3)$

$これと放物線 \ C\ との交点は \quad \cfrac{3}{8}x^2=x+2 \ \ を解いて \ \ x=4　\qquad よって \quad G(4,\ 6)$

$領域を右図のように分割すると$
\begin{eqnarray*} S_1 &=&台形BCDE -\cfrac{1}{4} \times (半径\sqrt{2} の円)-\triangle OAD -\triangle OBC\\ \\ &=&\cfrac{1}{2} \times (1+3) \times 2 -\cfrac{1}{4} \times \pi \times \sqrt{2}^2 - \cfrac{1}{2} \times 1 \times 1 - \cfrac{1}{2} \times 1 \times 1 \\ \\ &=&3-\cfrac{\pi}{2} \end{eqnarray*} \begin{eqnarray*} S_2 &=&\int_1^4 \{(x+2)-\cfrac{3}{8}x^2\}dx - \int_1^{\scriptsize{\cfrac{4}{3}}} \{(-x+2)-\cfrac{3}{8}x^2\}dx\\ \\ &=&\big[\cfrac{x^2}{2}+2x-\cfrac{x^3}{8}\big]_1^4 - \big[-\cfrac{x^2}{2} + 2x -\cfrac{x^3}{8}\big]_1^{\scriptsize{\cfrac{4}{3}}} \\ \\ &=&(8+8-8)-(\cfrac{1}{2}+2-\cfrac{1}{8})-\big\{(-\cfrac{8}{9}+\cfrac{8}{3}-\cfrac{8}{27})-(-\cfrac{1}{2}+2 -\cfrac{1}{8})\big\}\\ \\ &=&\cfrac{149}{27} \end{eqnarray*}
$求める領域の面積 \ S\ は \quad S=S_1+S_2=(3-\cfrac{\pi}{2})+\cfrac{149}{27}=\cfrac{230}{27}-\cfrac{\pi}{2}$

ページの先頭へ↑