$cos \cfrac{2k}{5}\pi, \ \ \sin \cfrac{2k}{5}\pi $ の値
$\theta =\cfrac{2k}{5}\pi \ \ (k\ は整数)\ に対して \quad \cos \theta,\quad \sin \theta \ \ の値を求めるには$
$z=\cos \theta +i\sin \theta \quad とおくと \quad z^5=\cos 5\theta +i\sin 5\theta =\cos 2k\pi +i\sin 2k\pi =1 \quad だから$
$z^5=1 \ \ をみたす \ \ z \ne 1 \ \ の解を求めれば、実部が \ \ \cos \theta、\ \ 虚部が \ \ \sin \theta \ \ として求まる。$
$そこで \ \ z\ を \ x\ に置き換えて \quad x^5=1\ \ (x \ne 1)\ の解を求めます。$
$x^5-1=(x-1)(x^4+x^3+x^2+x+1) \quad と因数分解されるから$
$x^4+x^3+x^2+x+1=0 \quad の解を求めればよい。\quad (このような対称形の方程式を相反方程式といいます)$
$x \ne 0 \quad だから 両辺を \ x^2\ で割って$
$x^2+x+1+\cfrac{1}{x}+\cfrac{1}{x^2}=0$
$(x^2+\cfrac{1}{x^2})+(x+\cfrac{1}{x})+1=0$
$(x+\cfrac{1}{x})^2+(x+\cfrac{1}{x})-1=0 $
$x+\cfrac{1}{x}=t \quad とおくと$
$t^2+t-1=0 \qquad \therefore \ \ t=\cfrac{-1 \pm \sqrt{5}}{2}$
(i)$\ \ t=\cfrac{-1 + \sqrt{5}}{2} \quad のとき$
$\quad x+\cfrac{1}{x}=\cfrac{-1 + \sqrt{5}}{2} $
$\quad x^2+\cfrac{1 - \sqrt{5}}{2}x+1=0$
$\quad x=\cfrac{-\dfrac{1-\sqrt{5}}{2} \pm \sqrt{\big(\dfrac{1-\sqrt{5}}{2}\big)^2-4}}{2}=\cfrac{\sqrt{5}-1}{4} \pm \cfrac{1}{2} \sqrt{\cfrac{5+\sqrt{5}}{2}}\ i$
(i)$\ \ t=\cfrac{-1 - \sqrt{5}}{2} \quad のとき$
$\quad x+\cfrac{1}{x}=\cfrac{-1 - \sqrt{5}}{2}$
$\quad x^2+\cfrac{1 + \sqrt{5}}{2}x+1=0$
$\quad x=\cfrac{-\dfrac{1+\sqrt{5}}{2} \pm \sqrt{\big(\dfrac{1+\sqrt{5}}{2}\big)^2-4}}{2}=-\cfrac{\sqrt{5}+1}{4} \pm \cfrac{1}{2} \sqrt{\cfrac{5-\sqrt{5}}{2}}\ i$
$よって 4\ つとも虚数解であることがわかりました。$
$x=\cos \cfrac{2k}{5}\pi +i\sin \cfrac{2k}{5}\pi \ \ (k\ は整数)\ だから$
$\omega =\cos \cfrac{2}{5}\pi + i\sin \cfrac{2}{5}\pi \quad とおくと解は \quad \ \omega , \ \ \omega ^2 ,\ \ \omega ^3, \ \ \omega ^4 $
$これらの解を複素数平面で表すと、右図のように正 \ 5\ 角形の頂点となります。$
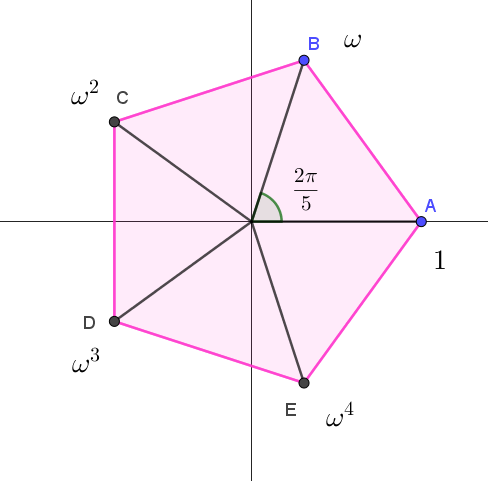
$\quad \omega =\cfrac{\sqrt{5}-1}{4} + \cfrac{1}{2} \sqrt{\cfrac{5+\sqrt{5}}{2}}i$
$\quad \omega ^2=-\cfrac{\sqrt{5}+1}{4} + \cfrac{1}{2} \sqrt{\cfrac{5-\sqrt{5}}{2}}i$
$\quad \omega ^3=-\cfrac{\sqrt{5}+1}{4} - \cfrac{1}{2} \sqrt{\cfrac{5-\sqrt{5}}{2}}i$
$\quad \omega ^4=\cfrac{\sqrt{5}-1}{4} - \cfrac{1}{2} \sqrt{\cfrac{5+\sqrt{5}}{2}}i$
$\omega =\cos \cfrac{2}{5}\pi + i\sin \cfrac{2}{5}\pi \quad より \quad \cos \cfrac{2}{5}\pi=\cfrac{\sqrt{5}-1}{4},\qquad \sin \cfrac{2}{5}\pi=\cfrac{1}{2} \sqrt{\cfrac{5+\sqrt{5}}{2}}$
$\omega ^2 =\cos \cfrac{4}{5}\pi + i\sin \cfrac{4}{5}\pi \quad より \quad \cos \cfrac{4}{5}\pi=-\cfrac{\sqrt{5}+1}{4},\qquad \sin \cfrac{4}{5}\pi=\cfrac{1}{2} \sqrt{\cfrac{5-\sqrt{5}}{2}}$
$\omega ^3 =\cos \cfrac{6}{5}\pi + i\sin \cfrac{6}{5}\pi \quad より \quad \cos \cfrac{6}{5}\pi=-\cfrac{\sqrt{5}+1}{4},\qquad \sin \cfrac{6}{5}\pi=-\cfrac{1}{2} \sqrt{\cfrac{5-\sqrt{5}}{2}}$
$\omega ^4 =\cos \cfrac{8}{5}\pi + i\sin \cfrac{8}{5}\pi \quad より \quad \cos \cfrac{8}{5}\pi=\cfrac{\sqrt{5}-1}{4},\qquad \sin \cfrac{8}{5}\pi=-\cfrac{1}{2} \sqrt{\cfrac{5+\sqrt{5}}{2}}$
$さらに$
$\cos \cfrac{2}{5}\pi=\cfrac{\sqrt{5}-1}{4} \quad より$
$2\cos ^2 \cfrac{\pi}{5} -1=\cfrac{\sqrt{5}-1}{4}$
$\cos ^2 \cfrac{\pi}{5} =\cfrac{\sqrt{5}+3}{8}=\cfrac{6+2\sqrt{5}}{16}=\cfrac{(\sqrt{5}+1)^2}{16}$
$\cos \cfrac{\pi}{5} > 0 \quad だから \quad \cos \cfrac{\pi}{5}=\cfrac{\sqrt{5}+1}{4}$
$\sin \cfrac{\pi}{5} =\sqrt{1-\cos ^2 \cfrac{\pi}{5}}=\sqrt{1-\cfrac{6+2\sqrt{5}}{16}}=\cfrac{\sqrt{10-2\sqrt{5}}}{4}$
メインメニュー に戻る