MY MATH NOTE

千葉大学(理系) 2022年　問題6

$座標空間において、原点 \ O\ と点 \ A(1,\ 0,\ -1)\ と点 \ B(0,\ 5,\ 0)\ がある。実数 \ t\ を用いて \ \ t\vec{OA}+\vec{OB}\ \ と$
$表される点全体を \ l\ とする。また、xy\ 平面上の \ y=x^2\ を満たす点全体からなる曲線を \ C\ とする。$
$(1)\ \ 曲線 \ C\ 上の点 \ P(a,\ a^2,\ 0)\ を固定する。l\ 上の点 \ Q\ を、\vec{OA}\ と \ \vec{PQ}\ が垂直であるようにとる。$
$\quad このとき、点 \ Q\ の座標を \ a\ を用いて表せ。$
$(2)\ \ 曲線 \ C上の点 \ R\ と \ l\ 上の点 \ S\ のうち、|\vec{RS}|\ を最小にする点 \ R\ と点 \ S\ の組み合わせをすべて求めよ。$
$\quad また、そのときの \ |\vec{RS}|\ の値を求めよ。$

(1)

　
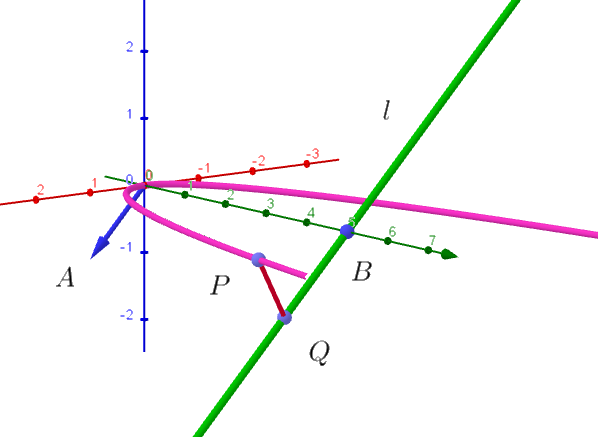
$点 \ Q\ は \ l\ 上にあるから$

$\quad \vec{OQ}=t\vec{OA}+\vec{OB}=t(1,\ 0,\ -1)+ (0,\ 5,\ 0)=(t,\ 5,\ -t)$

$\quad \vec{PQ}=\vec{OQ}-\vec{OP}=(t,\ 5,\ -t)- (a,\ a^2,\ 0)=(t-a,\ 5-a^2,\ -t)$

$\quad \vec{OA} \perp \vec{PQ} \quad より \quad \vec{OA} \cdot \vec{PQ}=0$

$\qquad 1 \times (t-a)+ 0 \times (5-a^2) -1 \times (-t)=0$

$\qquad 2t-a=0 \qquad t=\cfrac{a}{2}$

$\quad \therefore \ \ \vec{OQ}=(\cfrac{a}{2},\ 5,\ -\cfrac{a}{2}) \quad より \quad Q(\cfrac{a}{2},\ 5,\ -\cfrac{a}{2})$

(2)

　
$点\ R\ と \ l\ 上の点 \ S\ の距離(長さ)が最小になるのは$

$\quad RS \perp l \ \ のときである。$

$\qquad (これについては($点と直線の距離$)をご覧ください。)$

$R(x,\ x^2,\ 0) ,\ \ S(t,\ 5,\ -t) \quad とおくと \quad 　\vec{RS}=(t-x,\ 5-x^2,\ -t)$

$l\ の方向ベクトルは \quad \vec{d}=\vec{OA}=(1,\ 0,\ -1)$

$\vec{RS} \cdot \vec{d}=0 \quad より \quad (t-x) \times 1 + (5-x^2) \times 0 + (-t) \times (-1)=0 \qquad \therefore \ \ x=2t$

$\vec{RS}=(-t,\ 5-4t^2,\ -t) \quad だから \quad |\vec{RS}|^2=t^2+(5-4t^2)^2+t^2=16t^4-38t^2+25$

$f(t)=16t^4-38t^2+25 \quad とおくと $

$\quad f'(t)=64t^3-76t=4t(16t^2-19)$

$\quad f'(t)=0 \quad より \quad t=0,\quad \pm \cfrac{\sqrt{19}}{4}$

$\quad f(t)\ は偶関数であることに注意して$

\[ \begin{array}{c|c|c|c|c|c} t& \cdots & -\scriptsize{\cfrac{\sqrt{19}}{4}} & \cdots & 0 & \cdots & \scriptsize{\cfrac{\sqrt{19}}{4}} & \cdots \\ \hline f'(t)& - & 0 & + & 0 & - & 0 & + \\ \hline f(t)& \searrow & 極小 & \nearrow & 極大 & \searrow & 極小 & \nearrow \\ \end{array} \]
$\quad t=\pm \cfrac{\sqrt{19}}{4}\ \ で \ f(t)\ は極小かつ最小となり、f(t)\ の最小値は \quad f(\pm \cfrac{\sqrt{19}}{4})=16 \times (\cfrac{19}{16})^2-38 \times \cfrac{19}{16}+25=\cfrac{39}{16}$

$したがって$

$\quad \therefore \ \ R(\cfrac{\sqrt{19}}{2},\ \cfrac{19}{4},\ 0),\quad S(\cfrac{\sqrt{19}}{4},\ 5,\ -\cfrac{\sqrt{19}}{4})\quad と \quad R(-\cfrac{\sqrt{19}}{2},\ \cfrac{19}{4},\ 0),\quad S(-\cfrac{\sqrt{19}}{4},\ 5, \ \cfrac{\sqrt{19}}{4})$

$のとき、\quad |\vec{RS}|\ は最小で、最小値は \quad \cfrac{\sqrt{39}}{4}$


$(別解)$

$R(x,\ x^2,\ 0) ,\ \ S(t,\ 5,\ -t) \quad とおくと$
\begin{eqnarray*} |\vec{RS}|^2 &=&(t-x)^2+( 5-x^2)^2+(-t)^2\\ \\ &=&2t^2-2tx+x^4-9x^2+25\\ \\ &=&2(t-\cfrac{x}{2})^2+x^4-\cfrac{19}{2}x^2+25\\ \\ &=&2(t-\cfrac{x}{2})^2+(x^2-\cfrac{19}{4})^2+\cfrac{39}{16}\\ \end{eqnarray*} $よって、|\vec{RS}|\ \ は$

$\quad t=\cfrac{x}{2},\quad x^2=\cfrac{19}{4} \quad のとき、すなわち \quad x=\pm \cfrac{\sqrt{19}}{2},\quad t=\pm \cfrac{\sqrt{19}}{4} \quad のとき 最小値 \quad \cfrac{\sqrt{39}}{4} \quad をとる。$

$このとき$

$\quad \vec{RS}=(t-x,\ 5-x^2,\ -t)=(\mp \cfrac{\sqrt{19}}{4},\ \cfrac{1}{4},\ \mp \cfrac{\sqrt{19}}{4}) $

$\quad l\ の方向ベクトル \ \ \vec{d}\ は \ \ \vec{d}=\vec{OA}=(1,\ 0,\ -1)\ \ だから$

$\quad \vec{RS} \cdot \vec{d}=1 \times (\mp \cfrac{\sqrt{19}}{4}) + 0 \times \cfrac{1}{4} -1 \times (\mp \cfrac{\sqrt{19}}{4})=0 $

$となって \quad \vec{RS} \perp \vec{d} \quad すなわち \quad RS \perp l \quad がいえる。$

ページの先頭へ↑