千葉大学(医系)2018年前期 問題5
$複素数 \ \ z=\cos \cfrac{2\pi}{9}+i\sin \cfrac{2\pi}{9} \ \ に対し、\alpha = z+z^8 \ \ とおく。f(x)は整数係数の3次多項式で、3次の係数が1であり、$
$かつ \ f(\alpha)=0 \ \ となるものとする。ただし、すべての係数が整数である多項式を、整数係数の多項式という。$
$(1)\ f(x)を求めよ。ただし、f(x)\ がただ1つに決まることは証明しくてよい。$
$(2)\ 3次方程式\ f(x)=0\ \ の\alpha 以外の2つの解を、\alpha の2次以下の、整数係数の多項式の形で表せ。$
(1)
\begin{eqnarray*} \alpha &=&z+z^8\\ &=&\big(\cos \cfrac{2\pi}{9}+i\sin \cfrac{2\pi}{9}\big)+\big(\cos \cfrac{16\pi}{9}+i\sin \cfrac{16\pi}{9}\big)\\ &=&\{\cos \cfrac{2\pi}{9}+i\sin \cfrac{2\pi}{9}\}+\{\cos \big(2\pi-\cfrac{2\pi}{9}\big)+i\sin \big(2\pi-\cfrac{2\pi}{9}\big)\}\\ &=&\cos \cfrac{2\pi}{9}+i\sin \cfrac{2\pi}{9}+\cos \cfrac{2\pi}{9}-i\sin \cfrac{2\pi}{9}\\ &=&2\cos \cfrac{2\pi}{9}\\ \end{eqnarray*}$\theta=\cfrac{2\pi}{9} とおくと 3\theta=\cfrac{2\pi}{3} だから \cos 3\theta =\cos \cfrac{2\pi}{3}=-\cfrac{1}{2}$
$3倍角の公式より$
$\quad 4\cos ^3\theta - 3\cos \theta=-\cfrac{1}{2}$
$\quad (2\cos \theta )^3 - 3(2\cos \theta )+1 =0$
$\therefore \ \ \alpha ^3-3\alpha +1=0 すなわち \alpha \ \ は f(x)=x^3-3x+1=0 の解である。$
(2)
$f(x) をx-\alpha で割って商を求めると f(x)=(x-\alpha )(x^2+\alpha x+\alpha ^2-3)$
$f(x)=0 の \alpha 以外の解は x^2+\alpha x+\alpha ^2-3=0 を解いて$
\begin{eqnarray*} x&=&\cfrac{-\alpha \pm \sqrt{\alpha ^2 -4(\alpha ^2 -3)}}{2}\\ &=&\cfrac{-\alpha \pm \sqrt{12-3\alpha ^2}}{2}\\ &=&\cfrac{-2\cos \theta \pm \sqrt{12-12\cos ^2 \theta}}{2}\\ &=&\cfrac{-2\cos \theta \pm 2\sqrt{3}\sin \theta}{2}\\ &=&-\cos \theta \pm \sqrt{3}\sin \theta\\ \end{eqnarray*} $この2つの解を \ \ \beta , \ \gamma とおくと$
\begin{eqnarray*} \beta &=&-\cos \theta + \sqrt{3}\sin \theta\\ &=&-(\cos \theta - \sqrt{3}\sin \theta)\\ &=&-2\cos \big(\theta + \cfrac{\pi}{3}\big)\\ &=&-2\cos \big(\cfrac{2\pi}{9}+ \cfrac{\pi}{3}\big)\\ &=&-2\cos \cfrac{5\pi}{9}\\ &=&2\cos \big(\pi-\cfrac{5\pi}{9}\big)\\ &=&2\cos \cfrac{4\pi}{9}\\ &=&2\cos 2\theta \\ &=&2(2\cos ^2 \theta -1)\\ &=&4\cos ^2 \theta -2\\ &=&\alpha ^2 -2\\ \end{eqnarray*} $同様にして$
\begin{eqnarray*} \gamma &=&-\cos \theta - \sqrt{3}\sin \theta\\ &=&-(\cos \theta + \sqrt{3}\sin \theta)\\ &=&-2\cos \big(\theta - \cfrac{\pi}{3}\big)\\ &=&-2\cos \big(\cfrac{2\pi}{9}- \cfrac{\pi}{3}\big)\\ &=&-2\cos \cfrac{\pi}{9}\\ &=&2\cos \big(\pi-\cfrac{\pi}{9}\big)\\ &=&2\cos \cfrac{8\pi}{9}\\ &=&2\cos 4\theta \\ &=&2(2\cos ^2 2\theta -1)\\ &=&4\cos ^2 2\theta -2\\ &=&(2\cos 2\theta )^2-2\\ &=&(\alpha ^2 -2)^2 -2\\ &=&\alpha ^4 -4\alpha ^2 +2\\ &=&\alpha (\alpha ^3 -3\alpha +1)-\alpha ^2-\alpha +2\\ &=&-\alpha ^2-\alpha +2\\ \end{eqnarray*}
考察1
$一般に \cos n\theta \ \ が\ \ \cos \theta \ \ のn次式になることは$チェビシェフの多項式$を参考にしてください。$考察2
$x^3-3x+1=0 \ の解を直接求める方法は$3次方程式の実数解を求める方法$を参考にしてください。$$この方法で解いてみましょう$
$x^3-3x=-1$
$x=2y とおくと$
$\quad 8y^3 -6y=-1$
$\quad 4y^3 -3y=-\cfrac{1}{2}$
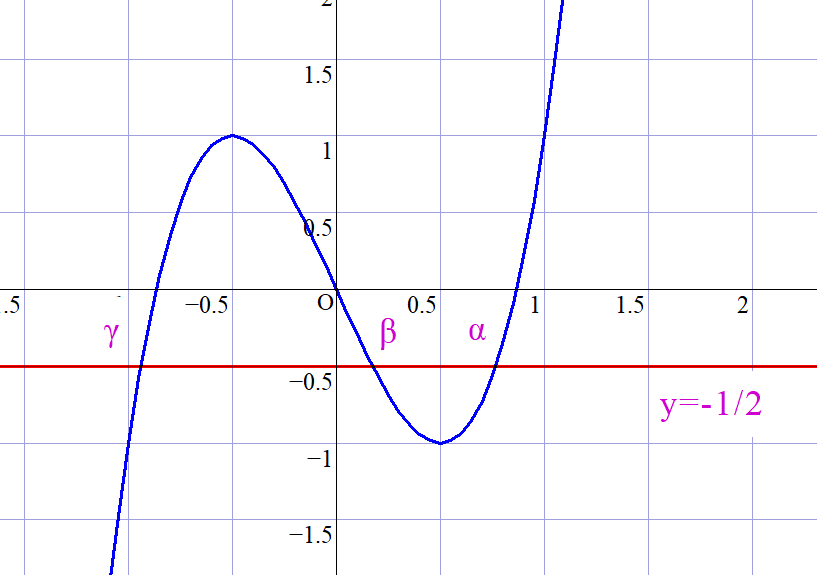
$右図のとおりで、異なる3点で交わるから$
$4y^3 -3y=-\cfrac{1}{2} は3つの実数解 \ \alpha , \beta , \gamma $
$をもち、解はすべて区間(-1,1)の中にある。$
$グラフの交点より$
$\qquad \cfrac{1}{2} < \alpha < 1,\ \ 0 < \beta < \cfrac{1}{2},\ \ -1 < \gamma < -\cfrac{1}{2} $
(i)$\ \ \cfrac{1}{2} < \alpha < 1 より \alpha =\cos \theta \ \ を満たす\theta が\ \ 0 < \theta < \cfrac{\pi}{3} \ \ に存在する。$
$\qquad 4\cos ^3 \theta -3\cos \theta =-\cfrac{1}{2} より \cos 3\theta =-\cfrac{1}{2}$
$\qquad 0 < 3\theta <\pi \ \ だから 3\theta =\cfrac{2\pi}{3} \qquad \theta=\cfrac{2\pi}{9} \qquad \therefore \alpha =\cos \cfrac{2\pi}{9}$
(ii)$\ \ \cos (3\theta +2\pi)=\cos 3\theta だから \cos 3(\theta +\cfrac{2\pi}{3})=-\cfrac{1}{2}$
$\qquad \theta '=\theta +\cfrac{2\pi}{3} とおくと \cos 3\theta' =-\cfrac{1}{2} だから \cos \theta ' \ \ も解である。$
$\qquad \theta '=\theta + \cfrac{2\pi}{3}=\cfrac{2\pi}{9}+\cfrac{2\pi}{3}=\cfrac{8\pi}{9}=4\theta $
$\qquad \cos \cfrac{8\pi}{9} < 0 だから \gamma =\cos \cfrac{8\pi}{9}=\cos 4 \theta $
(iii)$\ \ \cos (3\theta +4\pi)=\cos 3\theta だから \cos 3(\theta +\cfrac{4\pi}{3})=-\cfrac{1}{2}$
$\qquad \theta ''=\theta +\cfrac{4\pi}{3} とおくと \cos 3\theta''=-\cfrac{1}{2} だから \cos \theta '' \ \ も解である。$
$\qquad \theta ''=\theta + \cfrac{4\pi}{3}=\cfrac{2\pi}{9}+\cfrac{4\pi}{3}=\cfrac{14\pi}{9}=2\pi -\cfrac{4\pi}{9}$
$\qquad \cos \theta''=\cos \cfrac{4\pi}{9}=\cos 2\theta より \beta =\cos \cfrac{4\pi}{9}=\cos 2 \theta $
(i),(ii),(iii)$より 4y^3 -3y=-\cfrac{1}{2} の解は \cos \theta , \ \ \cos 2\theta , \ \ \cos 4\theta の3つである。$
$したがって x^3-3x+1=0 \ の解は x=2y より 2\cos \theta ,\quad 2\cos 2\theta ,\quad 2\cos 4 \theta である。$
メインメニュー に戻る