漸近線
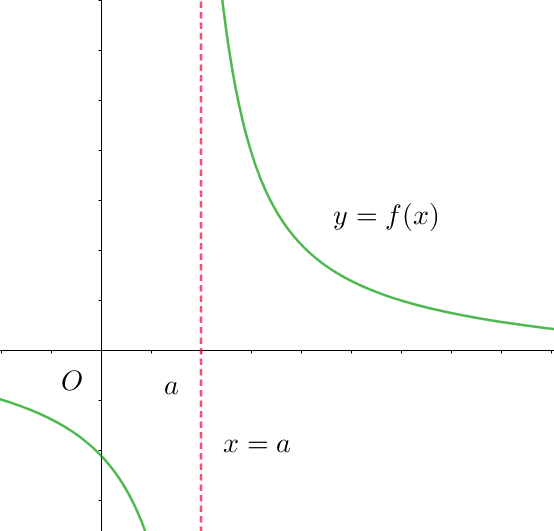
$(1)\ \ 漸近線とは$
$x \longrightarrow a +0 \quad あるいは \quad x \longrightarrow a -0 \quad のとき \quad y \longrightarrow +\infty$
$あるいは \quad y \longrightarrow -\infty \quad のとき、x=a \ を漸近線といいます。$
$また$
$x \longrightarrow \pm \infty \ \ のとき、曲線 \ y=f(x)\ \ が直線 \ \ y=mx+n \ \ に$
$限りなく近づくとき、この直線も \ y=f(x)\ の漸近線といい$
$ますが、この近づくとはどの長さのことでしょうか。$
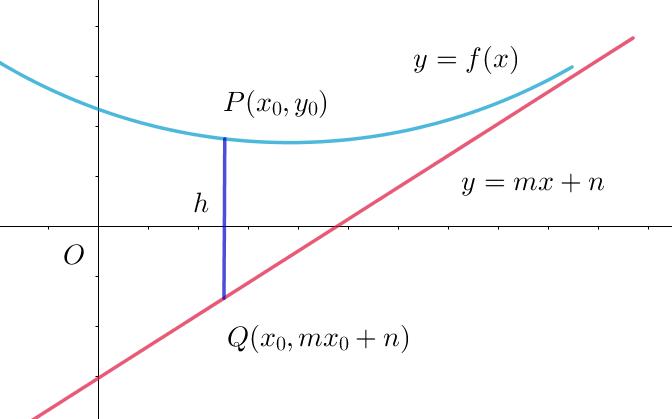
(i)$\ \ 通常右図の線分PQが使われます。$
$曲線 \ y=f(x)\ 上の点 \ P(x_0,\ y_0)\ に対して、$
$直線上の点 \ (x_0,\ mx_0+n)\ を \ Q\ とすると$
$\qquad h=PQ=|f(x_0)-(mx_0+n)|$
$この \ h\ が限りなく \ 0\ に近づくとき、y=mx+n\ を漸近線というわけです。$
$ところで、曲線 \ y=f(x)\ が直線 \ y=mx+n\ に限りなく近づくといったときはたしてこの \ h\ のことでしょうか。$
$おそらく、イメージとしては、点 \ P(x_0,\ y_0)\ と直線 \ y=mx+n \ の距離 \ d\ が限りなく \ 0\ に近づくことではないで$
$しょうか。$
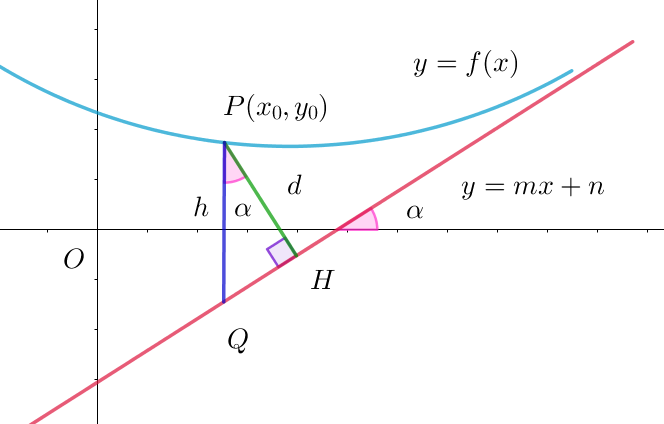
(ii)$\ \ 右図のような点 \ P\ と直線の距離 \ PH\ を考えた場合$
$m > 0\ \ として、この直線が \ x\ 軸の正方向となす角を$
$\alpha \ \ (0 < \alpha < \cfrac{\pi}{2})\ \ とすると \quad \tan \alpha =m$
$\angle QPH=\alpha \quad だから \quad \cos \alpha=\cfrac{d}{h}$
$\tan \alpha =m \quad より \quad \cos ^2 \alpha=\cfrac{1}{1+\tan ^2 \alpha}=\cfrac{1}{1+m^2} $
$\cos \alpha =\cfrac{1}{\sqrt{1+m^2}} \quad だから \quad \cfrac{d}{h}=\cfrac{1}{\sqrt{1+m^2}} $
$\therefore d=\cfrac{h}{\sqrt{1+m^2}} $
$よって \quad d \longrightarrow 0 \Longleftrightarrow h \longrightarrow 0$
$ですから、通常どおり \ h\ を考えればいいわけです。$
$なお、m < 0 \ \ の場合も全く同じです。$
$(2)\ \ 漸近線の求め方$
$y=mx+n \ \ が \ y=f(x)\ の漸近線であるとき$
\[\lim _{x \longrightarrow +\infty}(f(x)-mx-n) = 0 \quad だから \quad \lim _{x \longrightarrow +\infty}(f(x)-mx)-n = 0 \]
\[\therefore \ \ n=\lim _{x \longrightarrow +\infty}(f(x)-mx) \]
$このとき$
\[\lim _{x \longrightarrow +\infty}\big(\cfrac{f(x)}{x}-m \big) =\lim _{x \longrightarrow +\infty}\cfrac{f(x)-mx}{x} =
\lim _{x \longrightarrow +\infty}\cfrac{n}{x}=0\]
$したがって$
\[m= \lim _{x \longrightarrow +\infty}\cfrac{f(x)}{x}\]
\[この \ m\ を用いて \quad n=\lim _{x \longrightarrow +\infty}(f(x)-mx) \]
$例 \quad y=\sqrt{x^2-1}\ \ の漸近線を求めてみましょう。$
$偶関数だから \ \ x \geqq 0 \ \ で考える。$
\begin{eqnarray*}
m
&=&\lim _{x \longrightarrow +\infty}\cfrac{\sqrt{x^2-1}}{x}\\
&=&\lim _{x \longrightarrow +\infty}\sqrt{1-\frac{1}{x^2}}\\
\\
&=&1\\
\end{eqnarray*}
\begin{eqnarray*}
n
&=&\lim _{x \longrightarrow +\infty}(\sqrt{x^2-1}-x)\\
&=&\lim _{x \longrightarrow +\infty}\cfrac{(x^2-1)-x^2}{\sqrt{x^2-1}+x}\\
&=&\lim _{x \longrightarrow +\infty}\cfrac{-1}{\sqrt{x^2-1}+x}\\
&=&0\\
\end{eqnarray*}
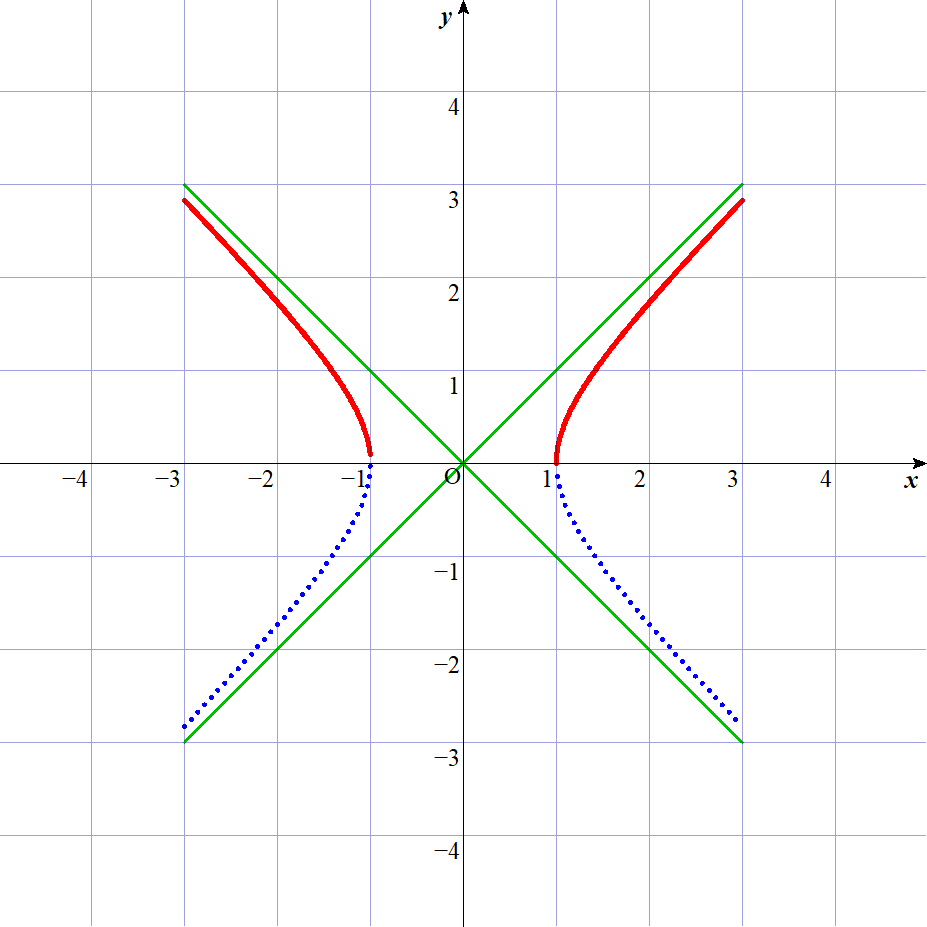
$y軸に関して対称であるから漸近線は \quad y=\pm x$
$なお、このグラフは \ \ x^2-y^2=1\ \ の \ \ y \geqq 0 \ \ の部分であるが$
$双曲線である。$
メインメニュー に戻る