相加・相乗平均の不等式(代数編)
$相加・相乗平均の不等式$
$\qquad 文字はすべて正とする$
$\hspace{4em} \cfrac{a_1+a_2+\cdots +a_n}{n} \geqq \large{\sqrt[n]{a_1a_2\cdots a_n}} \qquad \normalsize{ただし等号は} \quad a_1=a_2=\cdots =a_n \quad のとき$
$\qquad (解析的方法による証明は($相加・相乗平均の不等式(解析編)メニュー$)を参考にしてください。$
$(1)\ \ n=3\ \ の場合 \qquad \cfrac{a+b+c}{3} \geqq \sqrt[3]{abc}$
$(証明1)$
\begin{eqnarray*} & &A^3+B^3+C^3-3ABC\\ &=&(A+B+C)(A^2+B^2+C^2-AB-BC-CA)\\ &=&\cfrac{1}{2}(A+B+C)\{(A-B)^2+(B-C)^2+(C-A)^2\}\\ &\geqq&0\\ \end{eqnarray*} $\quad \therefore A^3+B^3+C^3 \geqq 3ABC \quad ただし等号は \ \ A=B=C\ \ のとき$
$\quad ここで、A^3=a,\quad B^3=b,\quad C^3=c \quad とおくと \quad a+b+c \geqq 3\sqrt[3]{a} \sqrt[3]{b}\sqrt[3]{c}$
$\quad よって \quad \cfrac{a+b+c}{3} \geqq \sqrt[3]{abc} \qquad 等号は \ \ a=b=c \ \ のとき$
$これは教科書によくある証明ですが、発展性は期待できません。$
$(証明2)$
$n=2\ \ の場合の \quad \cfrac{a+b}{2} \geqq \sqrt{ab} \quad は最重要な絶対不等式です。$
$n=4\ \ の場合は、n=2\ \ の不等式を \ 2\ 回繰り返して$
$\quad \cfrac{a+b+c+d}{4}=\cfrac{\dfrac{a+b}{2}+\dfrac{c+d}{2}}{2} \geqq \cfrac{\sqrt{ab}+\sqrt{cd}}{2} \geqq \sqrt{\sqrt{ab}\sqrt{cd}}=\sqrt[4]{abcd}$
$\quad \therefore \ \ \cfrac{a+b+c+d}{4} \geqq \sqrt[4]{abcd}$
$\quad 等号は \quad a=b,\ \ c=d \ \ かつ \ \ ab=cd \quad より \quad a=b=c=d \quad のとき$
$この \ \ n=4\ \ の場合を利用して \ \ n=3\ \ の場合を証明します。$
$\quad d=\cfrac{a+b+c}{3} \quad とおくと \quad \cfrac{a+b+c+d}{4} \geqq \large{\sqrt[4]{abcd}}\quad に \quad a+b+c=3d \quad を代入して$
$\quad d \geqq \large{\sqrt[4]{abcd}} \qquad d^4 \geqq abcd \quad より \quad d^3 \geqq abc $
$\quad d \geqq \large{\sqrt[3]{abc}} \quad \normalsize {すなわち} \quad \cfrac{a+b+c}{3} \geqq \large{\sqrt[3]{abc}}$
$誰が考えたかは知りませんが、実に巧妙な手です。この考え方が一般化できるのです。$
$これ以降、文字は \quad a_1,\ \ a_2, \ \ \cdots \quad と表します。$
$(2)\ \ n=5,\ \ 6,\ \ 7 \quad の場合$
$まず、n=8\ \ の場合を証明しますが、n=4 \ と \ n=2 \ の不等式を繰り返して$
$\quad \cfrac{a_1+a_2+a_3+a_4}{4} \geqq \large{\sqrt[4]{a_1a_2a_3a_4}} \qquad \normalsize{等号は} \quad a_1=a_2=a_3=a_4 \quad のとき$
$\quad \cfrac{a_5+a_6+a_7+a_8}{4} \geqq \large{\sqrt[4]{a_5a_6a_7a_8}} \qquad \normalsize{等号は} \quad a_5=a_6=a_7=a_8 \quad のとき$
$よって$
\begin{eqnarray*} & &\cfrac{a_1+a_2+a_3+a_4+a_5+a_6+a_7+a_8}{8}\\ \\ &=&\cfrac{\dfrac{a_1+a_2+a_3+a_4}{4}+\dfrac{a_5+a_6+a_7+a_8}{4}}{2}\\ \\ &\geqq &\cfrac{\large{\sqrt[4]{a_1a_2a_3a_4} + \sqrt[4]{a_5a_6a_7a_8}}}{2}\\ \\ &\geqq & \sqrt{\large{\sqrt[4]{a_1a_2a_3a_4}\sqrt[4]{a_5a_6a_7a_8}}}\\ \\ &=&\large{\sqrt[8]{a_1a_2a_3a_4a_5a_6a_7a_8}}\\ \end{eqnarray*}
$等号は \quad a_1=a_2=a_3=a_4、a_5=a_6=a_7=a_8 \quad かつ \quad a_1a_2a_3a_4=a_5a_6a_7a_8\quad より$
$\hspace{4em} a_1=a_2=a_3=a_4=a_5=a_6=a_7=a_8 \quad のとき$
$これで、n=2^3=8 \ \ の場合が証明できました。$
(i)$\ \ n=7 \quad の場合$
$\quad k=\cfrac{a_1+a_2+a_3+a_4+a_5+a_6+a_7}{7} \quad とおくと \quad \cfrac{a_1+a_2+a_3+a_4+a_5+a_6+a_7+k}{8} \geqq \large{\sqrt[8]{a_1a_2a_3a_4a_5a_6a_7k}}\quad に$
$\quad a_1+a_2+a_3+a_4+a_5+a_6+a_7=7k \quad を代入して \quad k \geqq \large{\sqrt[8]{a_1a_2a_3a_4a_5a_6a_7k}}$
$\quad k^8 \geqq a_1a_2a_3a_4a_5a_6a_7k \quad より \quad k^7 \geqq a_1a_2a_3a_4a_5a_6a_7$
$\quad k \geqq \large{\sqrt[7]{a_1a_2a_3a_4a_5a_6a_7}} \quad \normalsize{すなわち} \quad \cfrac{a_1+a_2+a_3+a_4+a_5+a_6+a_7}{7} \geqq \large{\sqrt[7]{a_1a_2a_3a_4a_5a_6a_7}}$
(ii)$\ \ n=6 \quad の場合$
$\quad k=\cfrac{a_1+a_2+a_3+a_4+a_5+a_6}{6} \quad とおくと \quad \cfrac{a_1+a_2+a_3+a_4+a_5+a_6+k+k}{8} \geqq \large{\sqrt[8]{a_1a_2a_3a_4a_5a_6k^2}} \quad に$
$\quad a_1+a_2+a_3+a_4+a_5+a_6=6k \quad を代入して \quad k \geqq \large{\sqrt[8]{a_1a_2a_3a_4a_5a_6k^2}}$
$\quad k^8 \geqq a_1a_2a_3a_4a_5a_6k^2 \quad より \quad k^6 \geqq a_1a_2a_3a_4a_5a_6$
$\quad k \geqq \large{\sqrt[6]{a_1a_2a_3a_4a_5a_6}} \quad \normalsize{すなわち} \quad \cfrac{a_1+a_2+a_3+a_4+a_5+a_6}{6} \geqq \large{\sqrt[6]{a_1a_2a_3a_4a_5a_6}}$
(iii)$\ \ n=5 \quad の場合$
$\quad k=\cfrac{a_1+a_2+a_3+a_4+a_5}{5} \quad とおくと \quad \cfrac{a_1+a_2+a_3+a_4+a_5+k+k+k}{8} \geqq \large{\sqrt[8]{a_1a_2a_3a_4a_5k^3}} \quad に$
$\quad a_1+a_2+a_3+a_4+a_5=5k \quad を代入して \quad k \geqq \large{\sqrt[8]{a_1a_2a_3a_4a_5k^3}}$
$\quad k^8 \geqq a_1a_2a_3a_4a_5k^3 \quad より \quad k^5 \geqq a_1a_2a_3a_4a_5$
$\quad k \geqq \large{\sqrt[5]{a_1a_2a_3a_4a_5}} \quad \normalsize{すなわち} \quad \cfrac{a_1+a_2+a_3+a_4+a_5}{5} \geqq \large{\sqrt[5]{a_1a_2a_3a_4a_5}}$
$このように、n=8=2^3 \ \ を証明すると \ \ n=7,\ \ 6,\ \ 5\ \ が全く同様に証明できることがわかります。$
$(3)\ \ n=2^p \quad (pは自然数)\ \ のとき成りたつことを数学的帰納法で証明します。$
(i)$\ \ p=1 \quad のとき$
$\qquad n=2 \ \ で \ \ \cfrac{a_1+a_2}{2} \geqq \sqrt{a_1a_2} \quad は成りたつ。$
(ii)$\ \ p=k\ \ のとき成りたつとすると$
$\hspace{3em} \cfrac{a_1+a_2+\cdots +a_{2^k}}{2^k} \geqq \large{\sqrt[2^k]{a_1a_2\cdots a_{2^k}}}$
$このとき$
\begin{eqnarray*} & &\cfrac{a_1+a_2+\cdots +a_{2^{k+1}}}{2^{k+1}}\\ \\ &=&\cfrac{1}{2}\cdot \cfrac{(a_1+a_2+\cdots +a_{2^k})+(a_{2^k+1}+a_{2^k+2}+\cdots +a_{2^k+2^k})}{2^k}\\ \\ &\geqq &\cfrac{1}{2}\big(\large{\sqrt[2^k]{a_1a_2 \cdots a_{2^k}}}+\large{\sqrt[2^k]{a_{2^k+1}a_{2^k+2} \cdots a_{2^k+2^k}}}\big)\\ \\ &\geqq &\sqrt{\large{\sqrt[2^k]{a_1a_2 \cdots a_{2^k} a_{2^k+1}a_{2^k+2} \cdots a_{2^{k+1}}}}}\\ \\ &\geqq &\large{\sqrt[2^{k+1}]{a_1a_2 \cdots a_{2^k} a_{2^k+1}a_{2^k+2} \cdots a_{2^{k+1}}}}\\ \end{eqnarray*}
$\quad よって \quad p=k+1\ \ のときも成りたつ。$
$\quad 等号は、明らかに \quad a_1=a_2= \cdots =a_{2^{k+1}} \quad のとき$
(i),(ii)$\ \ より \quad n=2^p\ \ のとき成りたつ。$
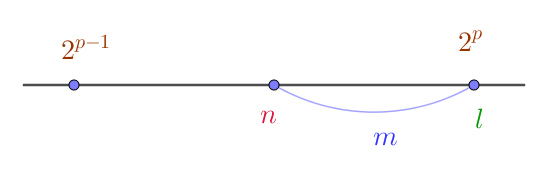
$(4)\ \ n\ が \ 2\ の累乗で表されない数のとき$
$\quad 2^{p-1} < n < 2^p \ \ を満たす最小の自然数 \ p\ をとり、2^p=l,\quad l-n=m \ \ とする。$
$\quad k=\cfrac{a_1+a_2+ \cdots +a_n}{n} \quad とおくと \quad \cfrac{a_1+a_2+\cdots a_n + \overbrace{k+k+\cdots +k}^{m個}}{l} \geqq \large{\sqrt[l]{a_1a_2 \cdots a_nk^m}}$
$\quad a_1+a_2+ \cdots + a_n=nk \quad を代入して \quad \cfrac{nk+mk}{l} \geqq \large{\sqrt[l]{a_1a_2 \cdots a_n k^m}}$
$\quad \cfrac{(n+m)k}{l} \geqq \sqrt[l]{a_1a_2 \cdots a_nk^m}\quad より \quad k \geqq \large{\sqrt[l]{a_1a_2 \cdots a_nk^m}}$
$\quad k^l \geqq a_1a_2 \cdots a_nk^m \quad だから \quad k^{l-m} \geqq a_1a_2 \cdots a_n \quad よって \quad k^n \geqq a_1a_2 \cdots a_n$
$\quad k \geqq \large{\sqrt[n]{a_1a_2 \cdots a_n}} \quad \normalsize{すなわち} \quad \cfrac{a_1+a_2+\cdots +a_n}{n} \geqq \large{\sqrt[n]{a_1a_2 \cdots a_n}}$
メインメニュー に戻る