フィボナッチ数列
1 フィボナッチ数列とは
$1202年、イタリアのフィボナッチは次のような問題を提起したとのことです。$
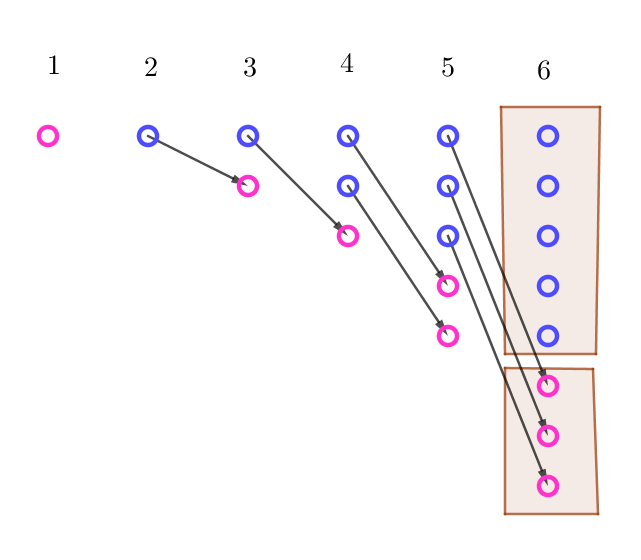
$1つがいのウサギは、生まれて2か月後から毎月1つがいずつの子どもを産む。$
$ウサギが死ぬことはないとして、生まれたばかりの1つがいのウサギは1年後には$
$何つがいのウサギになっているか。$
$右図で、赤丸は生まれた1つがいのウサギを表します。$
$nヶ月後のつがいの数を \ a_n\ とおくと \ \ a_1=1,\ \ a_2=1$
$3ヶ月後には、親とその子で \ 2\ つがいになるから、a_3=2$
$4ヶ月後には、親とその子および親がまた子どもを産むので \ 3\ つがいになるから、a_4=3$
$\quad 3=2+1\ \ で、2\ は \ 3ヶ月後の \ 2、1\ は \ 2ヶ月後の \ 1\ と考えられます。したがって \ \ a_4=a_3+a_2$
$5ヶ月後には、5\ つがいになり、a_5=5=3+2\ \ で、3\ は \ 4ヶ月後の \ 3、2\ は \ 3ヶ月後の \ 2\ だから \ \ a_5=a_4+a_3$
$6ヶ月後には、8\ つがいになり、a_6=8=5+3\ \ で、5\ は \ 5ヶ月後の \ 5、3\ は \ 4ヶ月後の \ 3\ だから \ \ a_6=a_5+a_4$
$\qquad \vdots$
$nヶ月後には、a_n=a_{n-1}+a_{n-2} \ \ が成りたつので、n=7,\ 8,\ \cdots ,\ 12\ を代入して順次 \ a_n を求めると$
$\quad 1,\ 1,\ 2,\ 3,\ 5,\ 8,\ 13,\ 21,\ 34,\ 55,\ 89,\ 144$
$よって \ \ 1\ 年後には \ 144\ つがいになっていることがわかります。$
$nヶ月後のつがいの総数を求める漸化式 \quad a_n=a_{n-1}+a_{n-2}\ \ で \ \ n \longrightarrow n+2 \ \ とおいて$
$\quad a_1=1,\ \ a_2=1,\ \ a_{n+2}=a_{n+1}+a_n \quad で求まる数列 \ \{a_n\}\ をフィボナッチ数列といいます。$
2 組合せ公式との関係
$(問題)\ \ 8\ 段の階段があるとき、1\ 歩で \ 1\ 段または \ 2\ 段上がるとする。8\ 段ちょうど上がりきる上がり方は$
$\qquad 何通りあるか。$
$n \geqq 3 \ \ のとき \ n\ 段の上がり方の総数を \ a_n \ 通りとする。$
$n=1\ のとき \ 1\ 歩で \ 1\ 段あがるのみであるから \quad a_1=1$
$n=2\ のとき \ 1\ 歩で \ 1\ 段ずつ \ 2\ 段あがるかまたは \ 1\ 歩で \ 2\ 段あがるかの \ 2\ 通りあるから \quad a_2=2$
$n\ 段の上がり方について$
$(1)\ \ 初めの \ 1\ 歩で \ 1\ 段上がるとき$
$\quad 残りの階段は \ n-1\ 段だからその上がり方の総数は \quad a_{n-1} \ \ とおり$
$(2)\ \ 初めの \ 1\ 歩で \ 2\ 段上がるとき$
$\quad 残りの階段は \ n-2\ 段だからその上がり方の総数は \quad a_{n-2}\ \ とおり$
$階段の上がり方は(1)または(2)のどちらかであるから \quad a_n=a_{n-1}+a_{n-2}$
$順次 \ a_n \ を求めると \quad 1,\ 2,\ 3,\ 5,\ 8,\ 13,\ 21,\ 34,\ \cdots $
$したがって \ 8\ 段の階段では \ 34\ 通りの上がり方がある。$
$項の番号が\ 1\ ずれていますが、これもフィボナッチ数列といいます。$
$この問題は次のように考えることもできます。$
$8\ 段上がるのに、1\ 段上がりが \ a\ 回、2\ 段上がりが \ b\ 回とすると \quad a+2b=8$
$これを満たす \ a,\ b\ は \quad (a,\ b)=(8,\ 0),\ (6, 1),\ (4,\ 2),\ (2,\ 3),\ (0,\ 4)\ \ である。$
$これらのうちたとえば \ (2,\ 3)\ については、5\ 歩のうち \ 1\ 段上がりが \ 2\ 回、2\ 段上がりが残り \ 3\ 回という$
$ことだからこの上がり方は \quad _5C_3\ 通りある。$
$このようにして、 8段の階段 の上がり方は全部で$
$\quad _8C_0 + _7C_1+_6C_2+_5C_3+_4C_4=1+7+15+10+1=34 \ (通り)$
$次に、なぜこの \ 2\ 通りの求め方が一致するのか考えてみましょう。$
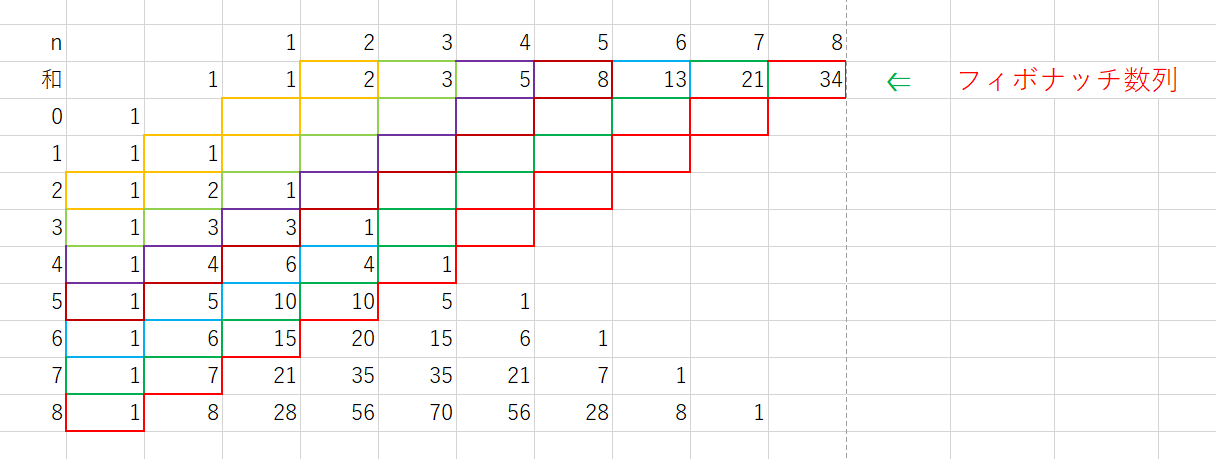
$右図は \ (a+b)^n \ の展開式の係数$
$を並べた表で、いわゆるパスカル$
$の三角形です。ただし、左端を揃$
$えています。$
$この表で、左下から右上に斜めに$
$並んだ数の和をとります。$
$紫枠で囲んだ数の和を \ a_5\ とおくと \quad a_5=1+4+3=8$
$青枠で囲んだ数の和を \ a_6\ とおくと \quad a_6=1+5+6+1=13$
$緑枠で囲んだ数の和を \ a_7\ とおくと \quad a_7=1+6+10+4=21$
$赤枠で囲んだ数の和を \ a_8\ とおくと \quad a_8=1+7+15+10+1=34$
$これらの数の並びは、フィボナッチ数列であることがわかります。a_8\ についてその理由を調べてみましょう。$
$\quad a_8=1+7+15+10+1==1+(1+6)+(5+10)+(6+4)+1=(1+6+10+4)+ (1+5+6+1)+=a_7+a_6$
$このように \ n=8\ についてフィボナッチ数列の漸化式が成りたつからです。$
$組合せの記号を用いてもう少し詳しく調べると$
$a_8=_8C_0+_7C_1+_6C_2+_5C_3+_4C_4 \quad において \quad _8C_0=_7C_0=1, \ \ _4C_4=_3C_3=1,\ \ _{n+1}C_r=_nC_{r-1}+_nC_r \quad だから$
\begin{eqnarray*}
a_8
&=&_8C_0+_7C_1+_6C_2+_5C_3+_4C_4\\
\\
&=&_7C_0+(_6C_0+_6C_1)+(_5C_1+_5C_2)+(_4C_2+_4C_3)+_3C_3\\
\\
&=&(_7C_0+_6C_1 + _5C_2 +_4C_3) + (_6C_0+_5C_1+_4C_2+_3C_3)\\
\\
&=&a_7+a_6
\end{eqnarray*}
$この方法で一般的に証明できます。$
$n\ が偶数のとき \ \ m=\cfrac{n}{2},\quad n\ が奇数のとき \ \ m=\cfrac{n+1}{2}\ \ として$
\begin{eqnarray*}
a_n
&=&_nC_0+_{n-1}C_1+_{n-2}C_2+_{n-3}C_3 + \cdots + _{m+1}C_{m-1}+_mC_m\\
\\
&=&_{n-1}C_0+(_{n-2}C_0+_{n-2}C_1)+(_{n-3}C_1+_{n-3}C_2)+(_{n-4}C_2+_{n-4}C_3)+\cdots +(_mC_{m-2}+_mC_{m-1})+_{m-1}C_{m-1}\\
\\
&=&(_{n-1}C_0+_{n-2}C_1 +_{n-3}C_2 +_{n-4}C_3 +\cdots + _mC_{m-1})+ (_{n-2}C_0 + _{n-3}C_1 +_{n-4}C_2+ \cdots + _mC_{m-2}+ _{m-1}C_{m-1})\\
\\
&=&a_{n-1}+a_{n-2}
\end{eqnarray*}
3 フィボナッチ数列の性質
$ここではフィボナッチ数列を \ \{F_n\}\ と表します。$
$(1)\quad F_1+F_2+\cdots +F_n=F_{n+2}-1$
$\quad (証明)$
$\quad F_{n+2}-F_{n+1}=F_n \quad で$
$\quad n=1\ \ とおくと \quad F_3-F_2=F_1$
$\quad n=2\ \ とおくと \quad F_4-F_3=F_2$
$\hspace{5em} \vdots $
$\quad n\ について \quad F_{n+2}-F_{n+1}=F_n$
$\quad 辺々加えて \quad F_{n+2}-F_2=F_1+F_2+ \cdots +F_n$
$\quad F_2=1 \ \ だから \ \ F_1+F_2+\cdots +F_n=F_{n+2}-1$
$(2)\quad F_1+F_3+\cdots +F_{2n-1}=F_{2n}$
$\quad (証明)$
$\quad F_{n+2}-F_n=F_{n+1} \ \ で$
$\quad n=2\ \ とおくと \quad F_4-F_2=F_3$
$\quad n=4\ \ とおくと \quad F_6-F_4=F_5$
$\hspace{5em}\vdots $
$\quad n\ を \ 2n-2\ \ とおくと \quad F_{2n}-F_{2n-2}=F_{2n-1}$
$\quad 辺々加えて \quad F_{2n}-F_2=F_3+F_5+ \cdots +F_{2n-1}$
$\quad F_2=F_1=1 \ \ だから \ \ F_1+F_3+\cdots +F_{2n-1}=F_{2n}$
$(3)\quad F_2+F_4+\cdots +F_{2n}=F_{2n+1}-1$
$\quad (証明)$
$\quad (2)と全く同じようにできます。$
$(4) \quad F_1^2+F_2^2+\cdots +F_n^2=F_nF_{n+1}$
$\quad (証明)$
$\quad F_{n+2}-F_n=F_{n+1} \ \ の両辺に \ F_{n+1}\ をかけて$
$\quad F_{n+1}F_{n+2}-F_nF_{n+1}=F_{n+1}^2$
$\quad n=1\ \ とおくと \quad F_2F_3-F_1F_2=F_2^2$
$\quad n=2\ \ とおくと \quad F_3F_4-F_2F_3=F_3^2$
$\hspace{5em} \vdots $
$\quad n\ を \ n-1\ \ とおくと \quad F_nF_{n+1}-F_{n-1}F_n=F_n^2$
$\quad 辺々加えて \quad F_nF_{n+1}-F_1F_2=F_2^2+F_3^2+ \cdots +F_n^2$
$\quad F_2=F_1=1 \ \ だから \ \ F_1^2+F_2^2+\cdots +F_n^2=F_nF_{n+1}$
$(5)\quad F_{n-1}F_{n+1}-F_n^2=(-1)^n \ \ (n \geqq 2)$
$\quad 数学的帰納法で証明$
(i)$\ \ n=2 \ \ のとき$
$\quad 左辺=F_1F_3-F_2^2=1\times 2-1^2=1 \qquad 右辺=(-1)^2=1$
$\quad よって \ n=2\ のとき成りたつ。$
(ii)$\ \ n=k \ のとき成りたつとすると \quad F_{k-1}F_{k+1}-F_k^2=(-1)^k$
$\quad このとき$
\begin{eqnarray*} & &F_kF_{k+2}-F_{k+1}^2\\ \\ &=&F_k(F_{k+1}+F_k)-F_{k+1}^2\\ \\ &=&F_k(2F_k+F_{k-1})-(F_k+F_{k-1})^2\\ \\ &=&F_k^2-F_{k-1}(F_k+F_{k-1})\\ \\ &=&F_k^2-F_{k-1}F_{k+1}\\ \\ &=&-(F_{k-1}F_{k+1}-F_k^2)\\ \\ &=&-(-1)^k\\ \\ &=&(-1)^{k+1} \end{eqnarray*} $\quad よって \ n=k+1\ のときも成りたつ。$
$\quad $(i),(ii)$より \ \ n \geqq 2 \ \ のすべての自然数 \ n\ について成りたつ。$
4 黄金比との関連
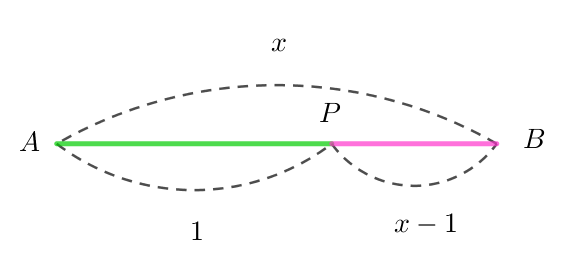
$黄金比、黄金分割はもともとユークリッドの原論に由来するものです。$
$第 \ 6\ 巻の定義 \ 3\ に外中比として取り上げられています。$
$線分 \ AB\ を \ AB:AP=AP:PB\ \ (ただし \ AP >PB)\ の比に分けることを$
$外中比に分けるといいます。$
$普通は全体を \ 1\ とおきますが、ここでは部分を \ 1\ とおきます。$
$\quad AP=1,\ \ AB=x \quad とおくと \quad x:1=1:(x-1) \qquad x(x-1)=1 \qquad \therefore \ \ x^2-x-1=0 $
$これを解いて \quad x=\cfrac{1+\sqrt{5}}{2}$
$この値を黄金数といい、\varphi \ \ であらわすと \quad \varphi=\cfrac{1+\sqrt{5}}{2}$
$\varphi^2=\varphi +1 \quad だから、この両辺に \ \ \varphi ^n \ \ をかけて$
$\varphi^{n+2}=\varphi ^{n+1} + \varphi ^n $
$この式をつかって計算を進めると$
$\varphi^2=\varphi +1 $
$\varphi^3=\varphi ^2 + \varphi =(\varphi +1)+ \varphi=2\varphi +1 $
$\varphi^4=\varphi ^3 + \varphi ^2 =(2\varphi +1)+ (\varphi +1)=3\varphi +2 $
$\varphi^5=\varphi ^4 + \varphi ^3 =(3\varphi +2)+ (2\varphi +1)=5\varphi +3 $
$\hspace{5em} \vdots $
$このように、\varphi の係数も定数項も \ \ 1,\ 1,\ 2,\ 3,\ 5,\cdots とフィボナッチ数列となりますから$
$\varphi ^{n+1}=F_{n+1} \varphi +F_n \quad と表されることがわかります。$
5 一般項の求め方
$a_1=1,\ \ a_2=1,\ \ a_{n+2}=a_{n+1}+ a_n \hspace{8em}(1)$
$\quad (1)が\quad a_{n+2}-\alpha a_{n+1}=\beta(a_{n+1}-\alpha a_n) \quad と変形できたとすると$
$a_{n+2}=(\alpha +\beta)a_{n+1}-\alpha \beta a_n $
$これが(1)に一致するためには \quad \alpha +\beta =1, \quad \alpha \beta =-1 $
$よって \ \ \alpha,\ \beta \ \ は \quad x^2-x-1=0 \quad すなわち \quad x^2=x+1 \ \ の解である。$
$これを(1)の特性方程式といいますが、黄金比の方程式に一致することがわかります。$
$すなわち、フィボナッチ数列と黄金比は本質的に結びついているわけです。$
$これを解いて \quad x= \cfrac{1 \pm \sqrt{5}}{2}$
(i)$\ \ \alpha= \cfrac{1 +\sqrt{5}}{2},\quad \beta= \cfrac{1 -\sqrt{5}}{2} \quad とおくと$
$\quad a_{n+2}-\alpha a_{n+1}=\beta(a_{n+1}-\alpha a_n)$
$\quad 数列 \ \{a_{n+1}-\alpha a_n\}\ は\ \ 公比 \ \beta \ の等比数列となるから$
$\quad a_{n+1}-\alpha a_n=\beta ^{n-1}(a_2-\alpha a_1)$
$\quad a_2-\alpha a_1=1-\alpha =\beta \quad より \quad a_{n+1}-\alpha a_n=\beta ^{n-1} \times \beta $
$\quad a_{n+1}-\alpha a_n=\beta ^n \hspace{15em}(2)$
(ii)$\ \ \alpha= \cfrac{1 - \sqrt{5}}{2},\quad \beta= \cfrac{1 +\sqrt{5}}{2} \quad とおくと$
$\quad 同様にして \quad a_{n+1}-\beta a_n=\alpha ^n \hspace{10em}(3)$
$(3)-(2)\ \ より \quad (\alpha -\beta) a_n=\alpha ^n - \beta ^n$
$\quad \alpha -\beta = (\cfrac{1 +\sqrt{5}}{2}) - (\cfrac{1 -\sqrt{5}}{2})=\sqrt{5} \quad だから$
$a_n=\cfrac{1}{\sqrt{5}}\big\{(\cfrac{1 +\sqrt{5}}{2})^n - (\cfrac{1 -\sqrt{5}}{2})^n\big\}$
$n=1\ \ とおくと \quad 右辺=\cfrac{1}{\sqrt{5}}\big\{(\cfrac{1 +\sqrt{5}}{2}) - (\cfrac{1 -\sqrt{5}}{2})\big\}=1=a_1$
$n=2\ \ とおくと \quad 右辺=\cfrac{1}{\sqrt{5}}\big\{(\cfrac{1 +\sqrt{5}}{2})^2 - (\cfrac{1 -\sqrt{5}}{2})^2\big\}=1=a_2$
$よって すべての自然数 \ n\ について \quad a_n=\cfrac{1}{\sqrt{5}}\big\{(\cfrac{1 +\sqrt{5}}{2})^n - (\cfrac{1 -\sqrt{5}}{2})^n\big\}$
6 隣接する2項の比の極限値
$a_n=\cfrac{1}{\sqrt{5}}\big\{(\cfrac{1 +\sqrt{5}}{2})^n - (\cfrac{1 -\sqrt{5}}{2})^n\big\}\ \ において \ \ \varphi=\cfrac{1 +\sqrt{5}}{2} ,\quad \psi =\cfrac{1 -\sqrt{5}}{2}\quad とおくと$
$a_n=\cfrac{1}{\sqrt{5}}(\varphi^n - \psi ^n)$
$\cfrac{a_{n+1}}{a_n}=\cfrac{\varphi ^{n+1}-\psi ^{n+1}}{\varphi ^n -\psi ^n }= \cfrac{\varphi -\psi (\dfrac{\psi}{\varphi})^n}{1-(\dfrac{\psi}{\varphi})^n}$
$\quad \cfrac{\psi}{\varphi}=\cfrac{1-\sqrt{5}}{1+\sqrt{5}}=\cfrac{(1-\sqrt{5})^2}{-4}=-\cfrac{3-\sqrt{5}}{2}\quad において$
$\quad 2 < \sqrt{5} < 3 \ \ より\ \ 0 < 3-\sqrt{5} < 1 \qquad \therefore \ \ -\cfrac{1}{2} < -\cfrac{3-\sqrt{5}}{2}<0 $
$よって \quad n \longrightarrow \infty \quad のとき \quad (\cfrac{\psi}{\varphi})^n \longrightarrow 0 \quad だから$
\[\lim _{n \rightarrow \infty}\cfrac{a_{n+1}}{a_n}=\varphi\] $したがって、フィボナッチ数列の隣接する \ 2\ 項の比の極限値は黄金数である。$
メインメニュー に戻る