15ゲーム
(1) 15ゲームの思い出
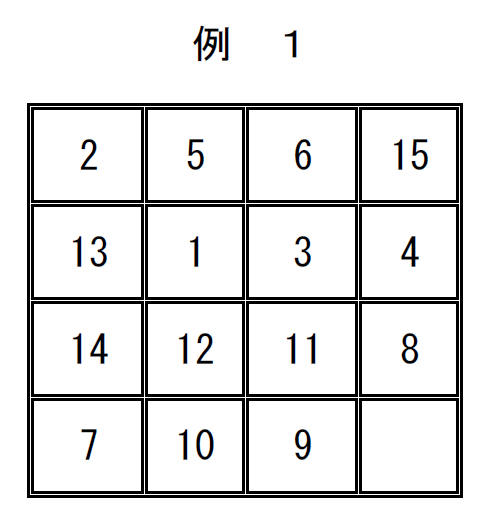
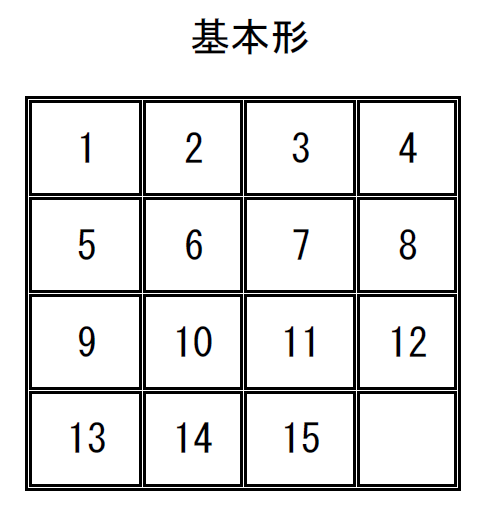
15ゲームとは、プラスチックや木で作られた4×4のますで、例1のように配置された
1から15の番号がついた駒を1つの空きスペースを使って、基本形のように並べ替える
ゲームのことです。
今では、パソコンやスマホでもアプリが探せます。
小学校5年生のとき、このゲームに夢中になったことを覚えています。
今と違って、学校に持って行っても取り上げられることはありませんでした。
あまりにも鼻高だったからか、担任の先生が、これをひっくり返して駒をバラバラにして、
適当にケースに戻し、これをやってみろと言われた。
ところが、最後の13,14,15の3駒がいくらやってもうまく並ばない。
内心おそらく不可能だろうと思ったが、その理由はわかりませんでした。
また。遊び方の説明書に、いくつかの完成図があったが、その中にもいくら頑張っても
できない完成図がありました。
とにかく最後の3駒の並び方でうまくできる場合と不可能な場合があることを経験的に
学びました。
そのときから55年経ちましたが、あのときの悔しさは今でも覚えています。
今は、なぜできる図とできない図があるのか私なりに理解できました。
この原稿では、それを明らかにしたいと思います。
(2) 15ゲームと置換
まずは、簡単に2 × 2ますで考えましょう。
左図が基本形になります。

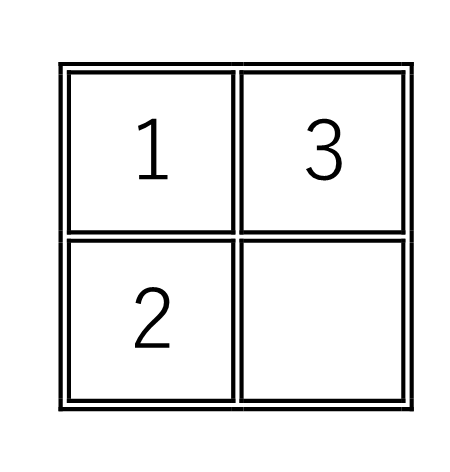
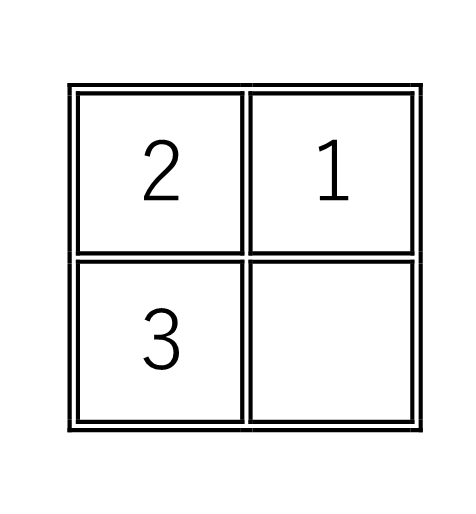
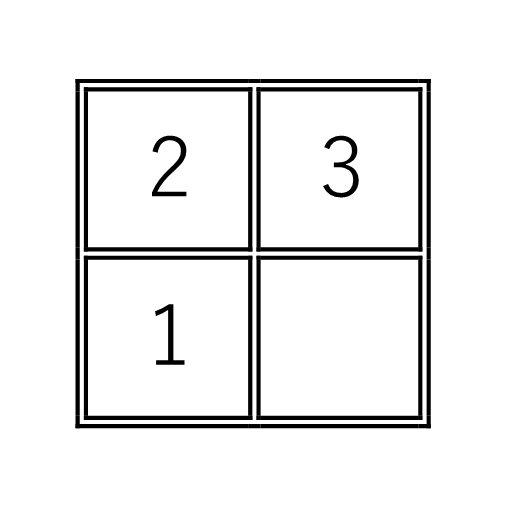
(ア)と(イ)からは決して基本形には戻れませんが、(ウ)からは戻れます。
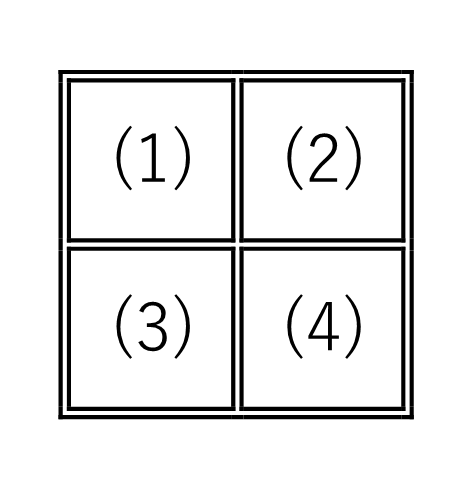
空白は(4)とします。
これらを置換を用いて表してみましょう。
$(ア)は \quad \left( \begin{array}{rr} 1 & 2 & 3 & 4 \\ 1 & 3 & 2 & 4 \\ \end{array} \right) = \left( \begin{array}{r} 2 & 3 \\ \end{array} \right)$
$(イ)は \quad \left( \begin{array}{rr} 1 & 2 & 3 & 4 \\ 2 & 1 & 3 & 4 \\ \end{array} \right) = \left( \begin{array}{r} 1 & 2 \\ \end{array} \right)$
$(ウ)は \quad \left( \begin{array}{rr} 1 & 2 & 3 & 4 \\ 2 & 3 & 1 & 4 \\ \end{array} \right) = \left( \begin{array}{r} 1 & 2 & 3 \\ \end{array} \right) = \left( \begin{array}{r} 1 & 2 \\ \end{array} \right) \left( \begin{array}{r} 1 & 3 \\ \end{array} \right)$
(ア)(イ)は奇置換、(ウ)は偶置換であることがわかります。
(ウ)について、空白の(4)を使って具体的に駒を動かしてみます。
1回目は3と4を交換します。
2回目は2と4を交換します。
3回目は1と4を交換します。
4回目は3と4を交換して、基本形に戻りました。
盤上では下のようになります。
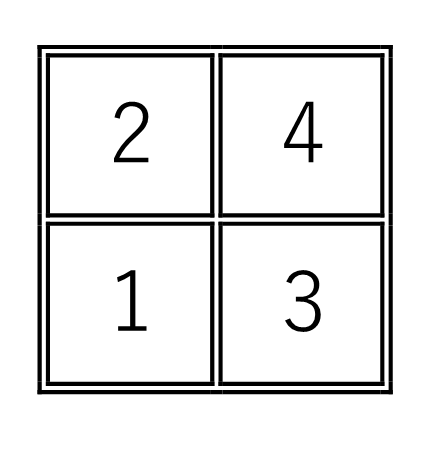
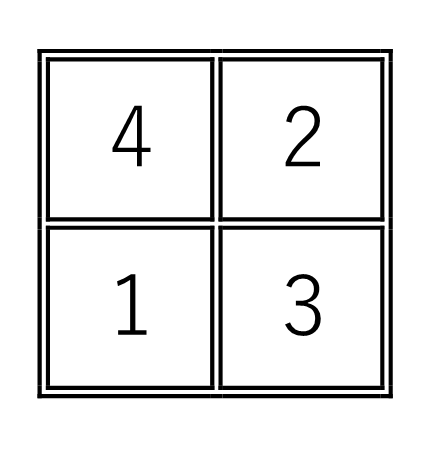
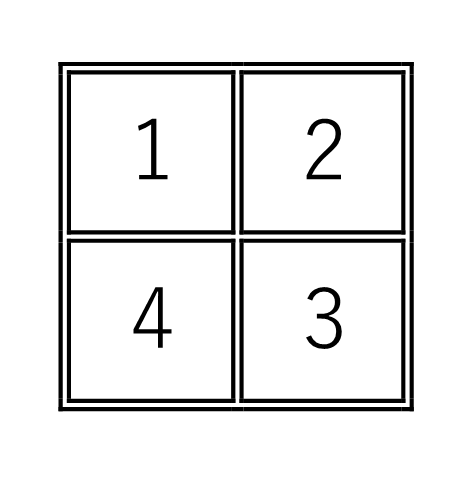

この駒の移動を置換で考えますと
$1回目は \quad \left( \begin{array}{rr} 1 & 2 & 3 & 4 \\ 2 & 3 & 1 & 4 \\ \end{array} \right) \left( \begin{array}{r} 3 & 4 \\ \end{array} \right) = \left( \begin{array}{rr} 1 & 2 & 3 & 4 \\ 2 & 4 & 1 & 3 \\ \end{array} \right) $
$2回目は \quad \left( \begin{array}{rr} 1 & 2 & 3 & 4 \\ 2 & 4 & 1 & 3 \\ \end{array} \right) \left( \begin{array}{r} 2 & 4 \\ \end{array} \right) = \left( \begin{array}{rr} 1 & 2 & 3 & 4 \\ 4 & 2 & 1 & 3 \\ \end{array} \right) $
$3回目は \quad \left( \begin{array}{rr} 1 & 2 & 3 & 4 \\ 4 & 2 & 1 & 3 \\ \end{array} \right) \left( \begin{array}{r} 1 & 4 \\ \end{array} \right) = \left( \begin{array}{rr} 1 & 2 & 3 & 4 \\ 1 & 2 & 4 & 3 \\ \end{array} \right) $
$4回目は \quad \left( \begin{array}{rr} 1 & 2 & 3 & 4 \\ 1 & 2 & 4 & 3 \\ \end{array} \right) \left( \begin{array}{r} 3 & 4 \\ \end{array} \right) = \left( \begin{array}{rr} 1 & 2 & 3 & 4 \\ 1 & 2 & 3 & 4 \\ \end{array} \right) $
$このように、駒と空白を交換することは、右からこの交換を表す置換をかけることに対応しますが、$
$(ウ)について、右から順に互換(3,4),\ (2,4),\ (1,4),\ (3,4)をかけて単位置換に変形したことになります。$
$ポイントは、偶置換に偶数回の互換を行ったことです。$
$では、なぜ偶数回の互換が必要だったのか。奇数回ではダメなのかを考えてみましょう。$
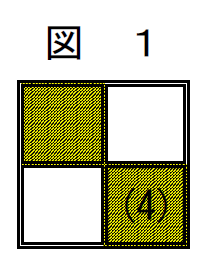
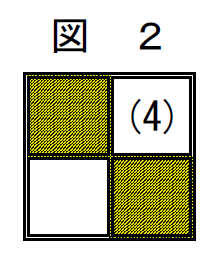
ある置換に1回互換を行うと、図1の空白(4)が図2のように1つ上か、もしくは左の白地に移ります。
次にもう一度互換を行うと、空白の(4)は白地からまた緑地に移ります。
このように、互換を行う度に、
緑地→白地→緑地→白地 ……
と繰り返しながら、最終的に右下の緑地にもどることになります。
この間に、「往って来い」で必ず偶数回の移動、すなわち互換が必要なわけです。
ただし、空白の位置が初めの状態と完成図で異なっている場合は、奇数回の移動で終了する
場合もあります。
したがって、最初の状態が
① 偶置換ならば、偶数回の互換で単位置換に直せる。
② 奇置換ならば、奇数回の互換で単位置換に直せる。
このことは、ますの数が3×3,4×4でも同じことです。
スマホの15ゲームの問題提示は、おそらく基本形の空白を乱数を用いて動かしていると思われ
るので、逆操作が存在するわけですから必ず元に戻せます。
ところが、盤から駒を取り出して並べ直すと、これが奇置換ならば、絶対に基本形に戻せません。
私の遠い昔の経験が、これで明らかになりました。
(3) 可能問題と不可能問題
初めの例1の16駒について、置換を調べてみましょう。
$\quad \left( \begin{array}{rr} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16\\ 2 & 5 & 6 & 15 & 13 & 1 & 3 & 4 & 14 & 12 & 11 & 8 & 7 & 10 & 9 & 16\\ \end{array} \right) $
$= \left( \begin{array}{r} 1 & 2 & 5 & 13 & 7 & 3 & 6 \\ \end{array} \right) \left( \begin{array}{r} 4 & 15 & 9 & 14 & 10 & 12 & 8 \\ \end{array} \right) \left( \begin{array}{r} 11 \\ \end{array} \right) \left( \begin{array}{r} 16 \\ \end{array} \right) $
$= \left( \begin{array}{r} 1 & 2 \\ \end{array} \right) \left( \begin{array}{r} 1 & 5 \\ \end{array} \right) \left( \begin{array}{r} 1 & 13 \\ \end{array} \right) \left( \begin{array}{r} 1 & 7 \\ \end{array} \right) \left( \begin{array}{r} 1 & 3 \\ \end{array} \right) \left( \begin{array}{r} 1 & 6 \\ \end{array} \right) \left( \begin{array}{r} 4 & 15 \\ \end{array} \right) \left( \begin{array}{r} 4 & 9 \\ \end{array} \right) \left( \begin{array}{r} 4 & 14\\ \end{array} \right) \left( \begin{array}{r} 4 & 10\\ \end{array} \right) \left( \begin{array}{r} 4 & 12\\ \end{array} \right) \left( \begin{array}{r} 4 & 8 \\ \end{array} \right) $
この問題の互換の数は12個と偶置換になります。
したがってこれを基本形に戻すことは可能です。
小学校の思い出で、最後の3駒の並び方でうまくできる場合と不可能な場合があることは
経験的にわかっていたのですが、次にそれを考えてみましょう。
13,14,15の3駒の並び方は6通りありますが、正解を除いた5通りは1から12の駒を省略して、
置換で表すと
$\qquad \left( \begin{array}{rr} 13 & 14 & 15 \\ 13 & 15 & 14 \\ \end{array} \right) = \left( \begin{array}{r} 14 & 15 \\ \end{array} \right) \ \ 奇置換だから不可能$
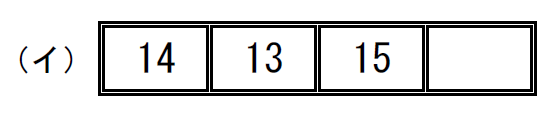
$\qquad \left( \begin{array}{rr} 13 & 14 & 15 \\ 14 & 13 & 15 \\ \end{array} \right) = \left( \begin{array}{r} 13 & 14 \\ \end{array} \right) \ \ 奇置換だから不可能$
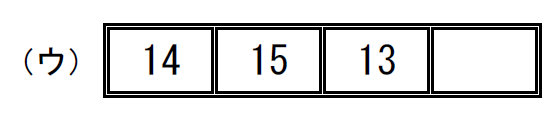
$\qquad \left( \begin{array}{rr} 13 & 14 & 15 \\ 14 & 15 & 13 \\ \end{array} \right) = \left( \begin{array}{r} 13 & 14 & 15 \\ \end{array} \right) = \left( \begin{array}{r} 13 & 14 \\ \end{array} \right) \left( \begin{array}{r} 13 & 15 \\ \end{array} \right)\ \ 偶置換だから可能$
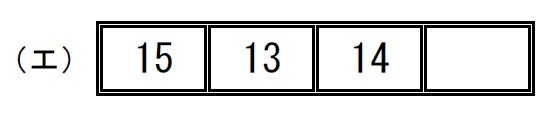
$\qquad \left( \begin{array}{rr} 13 & 14 & 15 \\ 15 & 13& 14 \\ \end{array} \right) = \left( \begin{array}{r} 13 & 15 & 14 \\ \end{array} \right) = \left( \begin{array}{r} 13 & 15 \\ \end{array} \right) \left( \begin{array}{r} 13 & 14 \\ \end{array} \right)\ \ 偶置換だから可能$
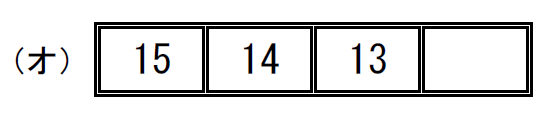
$\qquad \left( \begin{array}{rr} 13 & 14 & 15 \\ 15 & 14 & 13 \\ \end{array} \right) = \left( \begin{array}{r} 13 & 15 \\ \end{array} \right) \ \ 奇置換だから不可能$
こういうことだったのです。
(4) いろいろな完成図の可能性
最後に、遊び方の説明書にあった完成図について考えてみましょう。
基本形から、これらの完成図を作れるかが問題です。
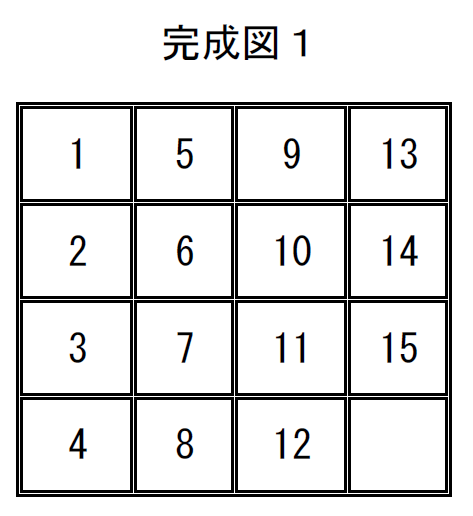
完成図1の置換は
$\quad \left( \begin{array}{rr} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16\\ 1 & 5 & 9 & 13 & 2 & 6 & 10 & 14 & 3 & 7 & 11 & 15 & 4 & 8 & 12 & 16\\ \end{array} \right)$
$= \left( \begin{array}{r} 2 & 5 \\ \end{array} \right) \left( \begin{array}{r} 3 & 9 \\ \end{array} \right) \left( \begin{array}{r} 4 & 13 \\ \end{array} \right) \left( \begin{array}{r} 7 & 10 \\ \end{array} \right) \left( \begin{array}{r} 8 & 14 \\ \end{array} \right) \left( \begin{array}{r} 12 & 15 \\ \end{array} \right)$
で、互換の数は6個と偶置換になりますので、基本形に戻せます。
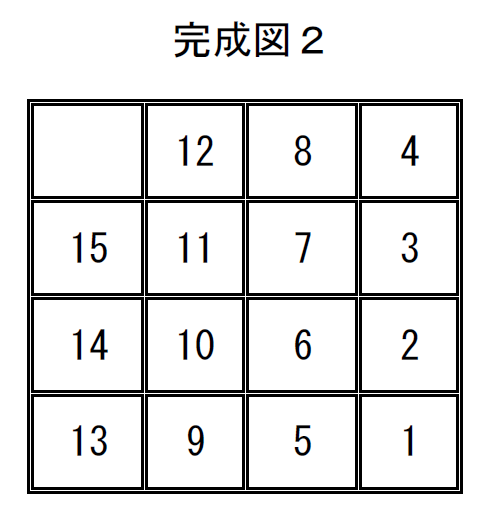
完成図2の置換は
$\quad \left( \begin{array}{rr} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16\\ 16 & 12 & 8 & 4 & 15 & 11 & 7 & 3 & 14 & 10 & 6 & 2 & 13 & 9 & 5 & 1\\ \end{array} \right)$
$= \left( \begin{array}{r} 1 & 16 \\ \end{array} \right) \left( \begin{array}{r} 2 & 12 \\ \end{array} \right) \left( \begin{array}{r} 3 & 8 \\ \end{array} \right) \left( \begin{array}{r} 5 & 15 \\ \end{array} \right) \left( \begin{array}{r} 6 & 11 \\ \end{array} \right) \left( \begin{array}{r} 9 & 14 \\ \end{array} \right)$
で、互換の数は6個と偶置換で、空白16の右下への移動も偶数回ですので基本形に戻せます。
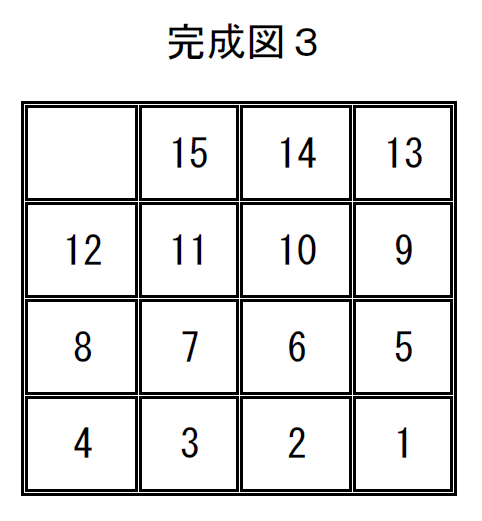
完成図3の置換は
$\quad \left( \begin{array}{rr} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16\\ 16 & 15 & 14 & 13 & 12 & 11 & 10 & 9 & 8 & 7 & 6 & 5 & 4 & 3 & 2 & 1\\ \end{array} \right)$
$= \left( \begin{array}{r} 1 & 16 \\ \end{array} \right) \left( \begin{array}{r} 2 & 15 \\ \end{array} \right) \left( \begin{array}{r} 3 & 14 \\ \end{array} \right) \left( \begin{array}{r} 4 & 13 \\ \end{array} \right) \left( \begin{array}{r} 6 & 12 \\ \end{array} \right) \left( \begin{array}{r} 6 & 11 \\ \end{array} \right) \left( \begin{array}{r} 7 & 10 \\ \end{array} \right) \left( \begin{array}{r} 8 & 9 \\ \end{array} \right)$
で、互換の数は8個と偶置換で、空白16の右下への移動も偶数回ですので基本形に戻せます。
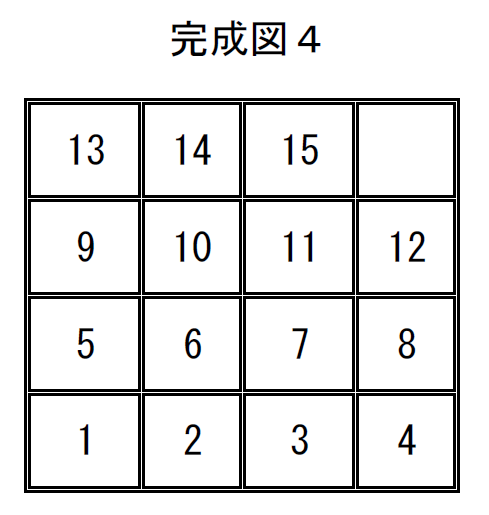
完成図4の置換は
$\quad \left( \begin{array}{rr} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16\\ 13 & 14 & 15 & 16 & 9 & 10 & 11 & 12 & 5 & 6 & 7 & 8 & 1 & 2 & 3 & 4\\ \end{array} \right)$
$= \left( \begin{array}{r} 1 & 13 \\ \end{array} \right) \left( \begin{array}{r} 2 & 14 \\ \end{array} \right) \left( \begin{array}{r} 3 & 15 \\ \end{array} \right) \left( \begin{array}{r} 4 & 16 \\ \end{array} \right) \left( \begin{array}{r} 5 & 9 \\ \end{array} \right) \left( \begin{array}{r} 6 & 10 \\ \end{array} \right) \left( \begin{array}{r} 7 & 11 \\ \end{array} \right) \left( \begin{array}{r} 8 & 12 \\ \end{array} \right)$
で、互換の数は8個と偶置換ですが、空白16の右下への移動は奇数回ですので
基本形に戻すことは不可能です。
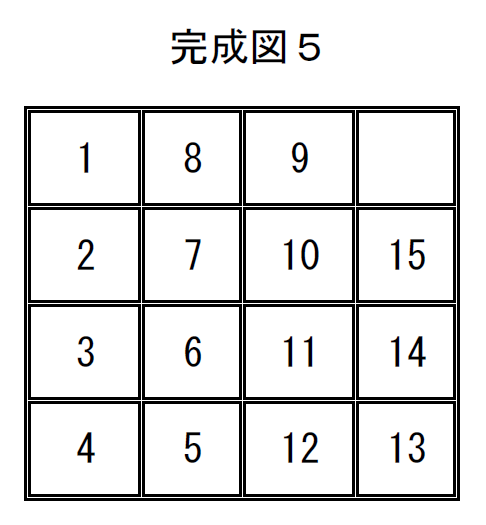
完成図5の置換は
$\quad \left( \begin{array}{rr} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16\\ 1 & 8 & 9 & 16 & 2 & 7 & 10 & 15 & 3 & 6 & 11 & 14 & 4 & 5 & 12 & 13\\ \end{array} \right) $
$= \left( \begin{array}{r} 2 & 8 & 15 & 12 & 14 & 5 \\ \end{array} \right) \left( \begin{array}{r} 3 & 9 \\ \end{array} \right) \left( \begin{array}{r} 4 & 16 & 13 \\ \end{array} \right) \left( \begin{array}{r} 6 & 7 & 10 \\ \end{array} \right) $
$= \left( \begin{array}{r} 2 & 8 \\ \end{array} \right) \left( \begin{array}{r} 2 & 15 \\ \end{array} \right) \left( \begin{array}{r} 2 & 12 \\ \end{array} \right) \left( \begin{array}{r} 2 & 14 \\ \end{array} \right) \left( \begin{array}{r} 2 & 5 \\ \end{array} \right) \left( \begin{array}{r} 3 & 9 \\ \end{array} \right) \left( \begin{array}{r} 4 & 16 \\ \end{array} \right) \left( \begin{array}{r} 4 & 13 \\ \end{array} \right) \left( \begin{array}{r} 6 & 7\\ \end{array} \right) \left( \begin{array}{r} 6 & 10\\ \end{array} \right)$
で、互換の数は10個と偶置換ですが、空白16の右下への移動は奇数回ですので
基本形に戻すことは不可能です。
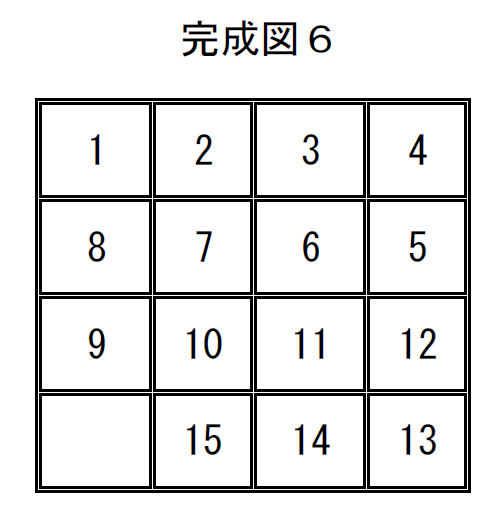
完成図6の置換は
$\quad \left( \begin{array}{rr} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16\\ 1 & 2 & 3 & 4 & 8 & 7 & 6 & 5 & 9 & 10 & 11 & 12 & 16 & 15 & 14 & 13\\ \end{array} \right)$
$= \left( \begin{array}{r} 5 & 8 \\ \end{array} \right) \left( \begin{array}{r} 6 & 7 \\ \end{array} \right) \left( \begin{array}{r} 13 & 16 \\ \end{array} \right) \left( \begin{array}{r} 14 & 15 \\ \end{array} \right)$
で、互換の数は4個と偶置換ですが、空白16の右下への移動は奇数回ですので
基本形に戻すことは不可能です。
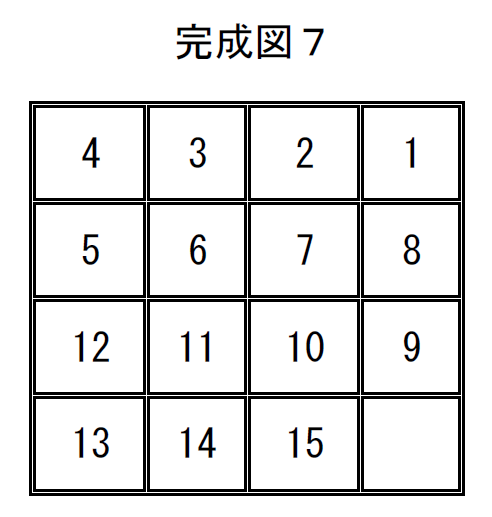
完成図7の置換は
$\quad \left( \begin{array}{rr} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16\\ 4 & 3 & 2 & 1 & 5 & 6 & 7 & 8 & 12 & 11 & 10 & 9 & 13 & 14 & 15 & 16\\ \end{array} \right)$
$= \left( \begin{array}{r} 1 & 4 \\ \end{array} \right) \left( \begin{array}{r} 2 & 3 \\ \end{array} \right) \left( \begin{array}{r} 9 & 12 \\ \end{array} \right) \left( \begin{array}{r} 10 & 11 \\ \end{array} \right)$
で、互換の数は4個と偶置換ですので、基本形に戻せます。
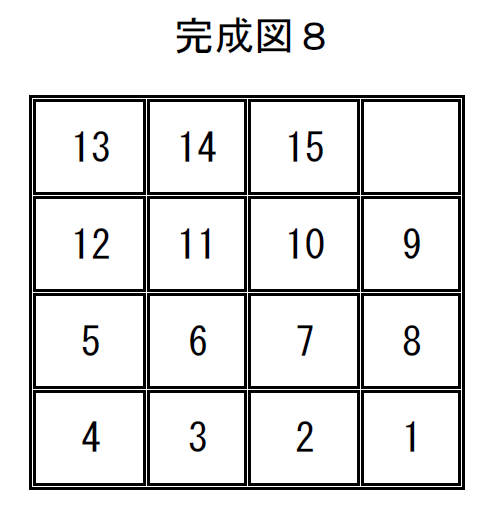
完成図8の置換は
$\quad \left( \begin{array}{rr} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16\\ 13& 14 & 15 & 16 & 12 & 11 & 10 & 9 & 5 & 6 & 7 & 8 & 4 & 3 & 2 & 1\\ \end{array} \right)$
$= \left( \begin{array}{r} 1 & 13 & 4 & 16 \\ \end{array} \right) \left( \begin{array}{r} 2 & 14 & 3 & 15 \\ \end{array} \right) \left( \begin{array}{r} 5 & 12 & 8 & 9 \\ \end{array} \right) \left( \begin{array}{r} 6 & 11 & 7 & 10 \\ \end{array} \right)$
$= \left( \begin{array}{r} 1 & 13 \\ \end{array} \right) \left( \begin{array}{r} 1 & 4 \\ \end{array} \right) \left( \begin{array}{r} 1 & 16 \\ \end{array} \right) \left( \begin{array}{r} 2 & 14 \\ \end{array} \right) \left( \begin{array}{r} 2 & 3 \\ \end{array} \right) \left( \begin{array}{r} 2 & 15 \\ \end{array} \right) \left( \begin{array}{r} 5 & 12 \\ \end{array} \right) \left( \begin{array}{r} 5 & 8 \\ \end{array} \right) \left( \begin{array}{r} 5 & 9 \\ \end{array} \right) \left( \begin{array}{r} 6 & 11 \\ \end{array} \right) \left( \begin{array}{r} 6 & 7 \\ \end{array} \right) \left( \begin{array}{r} 6 & 10 \\ \end{array} \right)$
で、互換の数は12個と偶置換ですが、空白16の右下への移動は奇数回ですので
基本形に戻すことは不可能です。
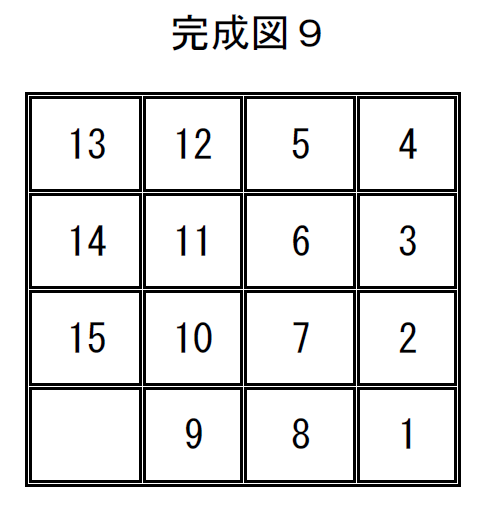
完成図9の置換は
$\quad \left( \begin{array}{rr} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16\\ 13& 12 & 5 & 4 & 14 & 11 & 6 & 3 & 15 & 10 & 7 & 2 & 16 & 9 & 8 & 1\\ \end{array} \right)$
$= \left( \begin{array}{r} 1 & 13 & 16 \\ \end{array} \right) \left( \begin{array}{r} 2 & 12 \\ \end{array} \right) \left( \begin{array}{r} 3 & 5 & 14 & 9 & 15 & 8\\ \end{array} \right) \left( \begin{array}{r} 6 & 11 & 7 \\ \end{array} \right)$
$= \left( \begin{array}{r} 1 & 13 \\ \end{array} \right) \left( \begin{array}{r} 1 & 16 \\ \end{array} \right) \left( \begin{array}{r} 2 & 12 \\ \end{array} \right) \left( \begin{array}{r} 3 & 5 \\ \end{array} \right) \left( \begin{array}{r} 3 & 14 \\ \end{array} \right) \left( \begin{array}{r} 3 & 9 \\ \end{array} \right) \left( \begin{array}{r} 3 & 15 \\ \end{array} \right) \left( \begin{array}{r} 3 & 8 \\ \end{array} \right) \left( \begin{array}{r} 6 & 11 \\ \end{array} \right) \left( \begin{array}{r} 6 & 7 \\ \end{array} \right)$
で、互換の数は10個と偶置換ですが、空白16の右下への移動は奇数回ですので
基本形に戻すことは不可能です。
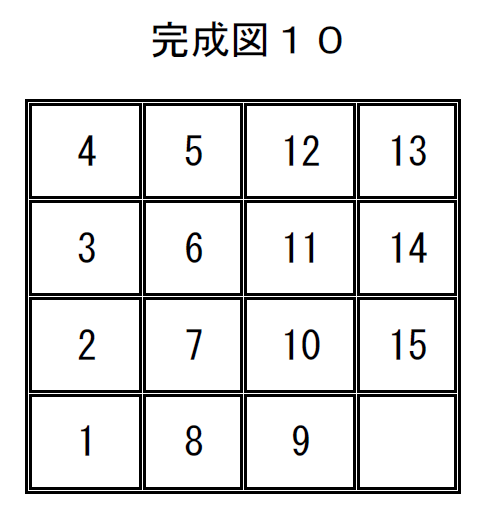
完成図10の置換は
$\quad \left( \begin{array}{rr} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16\\ 4 & 5 & 12 & 13 & 3 & 6 & 11 & 14 & 2 & 7 & 10 & 15 & 1 & 8 & 9 & 16\\ \end{array} \right)$
$= \left( \begin{array}{r} 1 & 4 & 13 \\ \end{array} \right) \left( \begin{array}{r} 2 & 5 & 3 & 12 & 15 & 9 \\ \end{array} \right) \left( \begin{array}{r} 7 & 11 & 10 \\ \end{array} \right) \left( \begin{array}{r} 8 & 14 \\ \end{array} \right)$
$= \left( \begin{array}{r} 1 & 4 \\ \end{array} \right) \left( \begin{array}{r} 1 & 13 \\ \end{array} \right) \left( \begin{array}{r} 2 & 5 \\ \end{array} \right) \left( \begin{array}{r} 2 & 3 \\ \end{array} \right) \left( \begin{array}{r} 2 & 12 \\ \end{array} \right) \left( \begin{array}{r} 2 & 15 \\ \end{array} \right) \left( \begin{array}{r} 2 & 9 \\ \end{array} \right) \left( \begin{array}{r} 7 & 11 \\ \end{array} \right) \left( \begin{array}{r} 7 & 10 \\ \end{array} \right) \left( \begin{array}{r} 8 & 14 \\ \end{array} \right)$
で、互換の数は10個と偶置換ですので、基本形に戻せます。
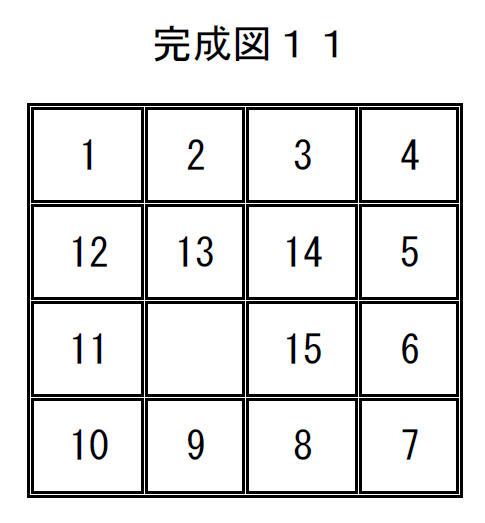
完成図11の置換は
$\quad \left( \begin{array}{rr} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16\\ 1 & 2 & 3 & 4 & 12 & 13 & 14 & 5 & 11 & 16 & 15 & 6 & 10 & 9 & 8 & 7\\ \end{array} \right)$
$= \left( \begin{array}{r} 5 & 12 & 6 & 13 & 10 & 16 & 7 & 14 & 9 & 11 & 15 & 8 \\ \end{array} \right)$
$= \left( \begin{array}{r} 5 & 12 \\ \end{array} \right) \left( \begin{array}{r} 5 & 6 \\ \end{array} \right) \left( \begin{array}{r} 5 & 13 \\ \end{array} \right) \left( \begin{array}{r} 5 & 10 \\ \end{array} \right) \left( \begin{array}{r} 5 & 16 \\ \end{array} \right) \left( \begin{array}{r} 5 & 7 \\ \end{array} \right) \left( \begin{array}{r} 5 & 14 \\ \end{array} \right) \left( \begin{array}{r} 5 & 9 \\ \end{array} \right) \left( \begin{array}{r} 5 & 11 \\ \end{array} \right) \left( \begin{array}{r} 5 & 15 \\ \end{array} \right) \left( \begin{array}{r} 5 & 8 \\ \end{array} \right)$
で、互換の数は11個と奇置換ですが、空白16の右下への移動は奇数回ですので
基本形に戻せます。
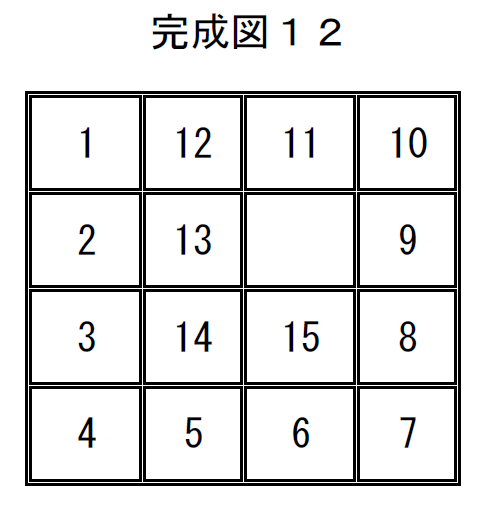
完成図12の置換は
$\quad \left( \begin{array}{rr} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16\\ 1 & 12 & 11 & 10 & 2 & 13 & 16 & 9 & 3 & 14 & 15 & 8 & 4 & 5 & 6 & 7\\ \end{array} \right)$
$= \left( \begin{array}{r} 2 & 12 & 8 & 9 & 3 & 11 & 15 & 6 & 13 & 4 & 10 & 14 & 5 \\ \end{array} \right) \left( \begin{array}{r} 7 & 16 \\ \end{array} \right)$
$= \left( \begin{array}{r} 2 & 12 \\ \end{array} \right) \left( \begin{array}{r} 2 & 8 \\ \end{array} \right) \left( \begin{array}{r} 2 & 9 \\ \end{array} \right) \left( \begin{array}{r} 2 & 3 \\ \end{array} \right) \left( \begin{array}{r} 2 & 11 \\ \end{array} \right) \left( \begin{array}{r} 2 & 15 \\ \end{array} \right) \left( \begin{array}{r} 2 & 6 \\ \end{array} \right) \left( \begin{array}{r} 2 & 13 \\ \end{array} \right) \left( \begin{array}{r} 2 & 4 \\ \end{array} \right) \left( \begin{array}{r} 2 & 10 \\ \end{array} \right) \left( \begin{array}{r} 2 & 14 \\ \end{array} \right) \left( \begin{array}{r} 2 & 5 \\ \end{array} \right) \left( \begin{array}{r} 7 & 16 \\ \end{array} \right)$
で、互の数は13個と奇置換ですが、空白16の右下への移動は奇数回ですので
基本形に戻せます。
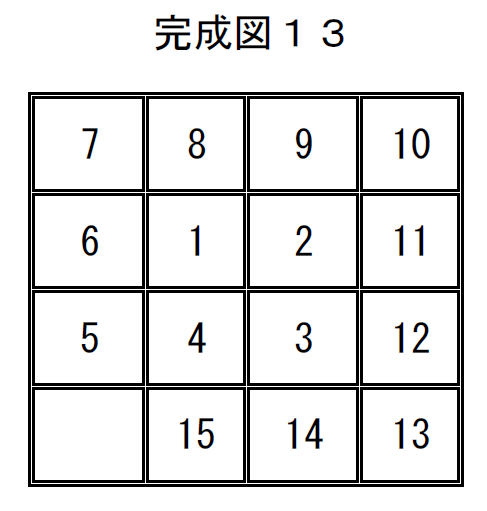
完成図13の置換は
$\quad \left( \begin{array}{rr} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16\\ 7 & 8 & 9 & 10 & 6 & 1 & 2 & 11 & 5 & 4 & 3 & 12 & 16 & 15 & 14 & 13\\ \end{array} \right)$
$= \left( \begin{array}{r} 1 & 7 & 2 & 8 & 11 & 3 & 9 & 5 & 6 \\ \end{array} \right) \left( \begin{array}{r} 4 & 10 \\ \end{array} \right) \left( \begin{array}{r} 13 & 16 \\ \end{array} \right) \left( \begin{array}{r} 14 & 15 \\ \end{array} \right)$
$= \left( \begin{array}{r} 1 & 7 \\ \end{array} \right) \left( \begin{array}{r} 1 & 2 \\ \end{array} \right) \left( \begin{array}{r} 1 & 8 \\ \end{array} \right) \left( \begin{array}{r} 1 & 11 \\ \end{array} \right) \left( \begin{array}{r} 1 & 3 \\ \end{array} \right) \left( \begin{array}{r} 1 & 9 \\ \end{array} \right) \left( \begin{array}{r} 1 & 5 \\ \end{array} \right) \left( \begin{array}{r} 1 & 6 \\ \end{array} \right) \left( \begin{array}{r} 4 & 10 \\ \end{array} \right) \left( \begin{array}{r} 13 & 16 \\ \end{array} \right) \left( \begin{array}{r} 14 & 15 \\ \end{array} \right)$
で、互換の数は11個と奇置換ですが、空白16の右下への移動は奇数回ですので
基本形に戻せます。
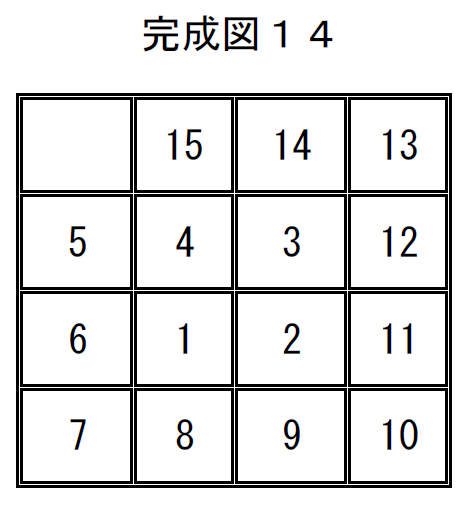
完成図14の置換は
$\quad \left( \begin{array}{rr} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16\\ 16 & 15 & 14 & 13 & 5 & 4 & 3 & 12 & 6 & 1 & 2 & 11 & 7 & 8 & 9 & 10\\ \end{array} \right)$
$= \left( \begin{array}{r} 1 & 16 & 10 \\ \end{array} \right) \left( \begin{array}{r} 2 & 15 & 9 & 6 & 4 & 13 & 7 & 3 & 14 & 8 & 12 & 11 \\ \end{array} \right)$
$= \left( \begin{array}{r} 1 & 16 \\ \end{array} \right) \left( \begin{array}{r} 1 & 10 \\ \end{array} \right) \left( \begin{array}{r} 2 & 15 \\ \end{array} \right) \left( \begin{array}{r} 2 & 9 \\ \end{array} \right) \left( \begin{array}{r} 2 & 6 \\ \end{array} \right) \left( \begin{array}{r} 2 & 4 \\ \end{array} \right) \left( \begin{array}{r} 2 & 13 \\ \end{array} \right) \left( \begin{array}{r} 2 & 7 \\ \end{array} \right) \left( \begin{array}{r} 2 & 3 \\ \end{array} \right) \left( \begin{array}{r} 2 & 14 \\ \end{array} \right) \left( \begin{array}{r} 2 & 8 \\ \end{array} \right) \left( \begin{array}{r} 2 & 12 \\ \end{array} \right) \left( \begin{array}{r} 2 & 11 \\ \end{array} \right)$
で、互換の数は13個と奇置換ですが、空白16の右下への移動は偶数回ですので
基本形に戻すことは不可能です。
このように、始めの並べ方はいろいろありますが、最終的に基本形に戻せる形と、戻せない形があるわけです。
小生の記憶が正しければ、これら戻せない形も説明書に載っていたことになります。
わかってしまうと、なにか夢がしぼんでしまいました。
メインメニュー に戻る