横浜国立大学(理系) 2025年 問題5
$xy平面上の曲線 \ C:x=y^2 \ を考える。実数 \ t\ に対して、曲線 \ C\ 上の点(t^2,\ t)\ における \ C\ の法線を \ \ell \ とする。$
$次の問いに答えよ。$
$(1)\ \ 法線 \ \ell \ の方程式を求めよ。$
$(2)\ \ 曲線 \ C\ と直線 \ x=1 \ で囲まれる領域を \ D\ とする。また、実数 \ t\ が \ t \leqq 0 \ をみたしながら動くとき、法線$
$\quad \ell \ が通過する領域を \ E\ とする。D\ と \ E\ の共通部分を求め、図示せよ。$
$(3)\ \ (2) で求めた \ D\ と \ E\ の共通部分の面積を求めよ。$
(1)

$あるいは、x\ で微分して \quad 1=2y\dfrac{dy}{dx} \qquad \dfrac{dy}{dx}=\dfrac{1}{2y}$
$曲線 \ C\ 上の点(t^2,\ t)\ における \ C\ の接線の傾きは \ \ \dfrac{1}{2t} \quad だから$
$これに直交する法線の傾きは \quad -2t$
$法線 \ \ell \ の方程式は \quad y=-2t(x-t^2)+t $
$すなわち \quad y=-2tx+2t^3+t$
(2)

$\ell \ が通過する領域は見てとれるので、逆に通過しない領域を調べる$
$ことにする。$
$一般に、曲線 \ L\ が曲線群 \ C:f(x,y,t)=0 \ \ (t\ はパラメータ)\ と、$
$ある点で接するとき、L\ を \ C\ の包絡線といいます。$
$したがって、直線群が決して通らない領域の境界が包絡線になります。$
$ \qquad 詳しくは($包絡線$)をご覧ください。$
$この問題の包絡線 \ L\ の求め方は$
$直線群 \ \ y=-2tx+2t^3+t \hspace{7em}①$
$①を \ x\ で微分して \quad \dfrac{dy}{dx}=-2t \hspace{5em}②$
$\dfrac{dy}{dx}=\dfrac{\dfrac{dy}{dt}}{\dfrac{dx}{dt}}=-2t \quad だから$
$\dfrac{dy}{dt}=-2t\dfrac{dx}{dt} \hspace{5em}③$
$①を \ t\ で微分して \quad \dfrac{dy}{dt}=-2x-2t\dfrac{dx}{dt} +6t^2+1$
$③を代入して \quad -2t\dfrac{dx}{dt}=-2x-2t\dfrac{dx}{dt} +6t^2+1$
$\therefore \ \ 6t^2=2x-1 \quad t \leqq 0 \quad だから$
$t=-\sqrt{\dfrac{2x-1}{6}}$
$①に代入して$
$y=\sqrt{\dfrac{2x-1}{6}}(2x- \dfrac{2x-1}{3} -1)$
$y=\dfrac{2}{3}(2x-1)\sqrt{\dfrac{2x-1}{6}}$
$y=\dfrac{\sqrt{6}}{9}(2x-1)^{\scriptsize{\dfrac{3}{2}}}$
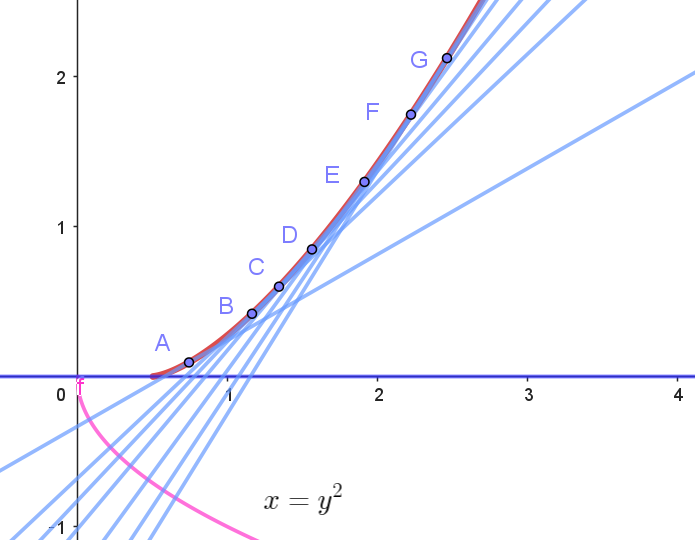
$これが、直線群 \ \ell \ が通過する、しないの境界をあらわす包絡線である。$
$右図からわかるとおり、領域 \ E\ は、x\ 軸の下と包絡線の下の部分である。$

(3)
$求める面積を \ S\ とすると$
\begin{eqnarray*} S &=&\int_{\scriptsize{\dfrac{1}{2}}}^1 \dfrac{\sqrt{6}}{9}(2x-1)^{\scriptsize{\dfrac{3}{2}}}dx + \int_0^1 \sqrt{x} dx\\ \\ &=&\dfrac{\sqrt{6}}{9} \times \dfrac{2}{5} \times \dfrac{1}{2} \big[(2x-1)^{\scriptsize{\dfrac{5}{2}}}\big]_{\scriptsize{\dfrac{1}{2}}}^1 + \dfrac{2}{3}\big[x^{\scriptsize{\dfrac{3}{2}}}\big]_0^1 \\ \\ &=&\dfrac{\sqrt{6}}{45} + \dfrac{2}{3}\\ \\ &=&\dfrac{30+ \sqrt{6}}{45} \end{eqnarray*}
メインメニュー に戻る