横浜国立大学(理系) 2025年 問題3
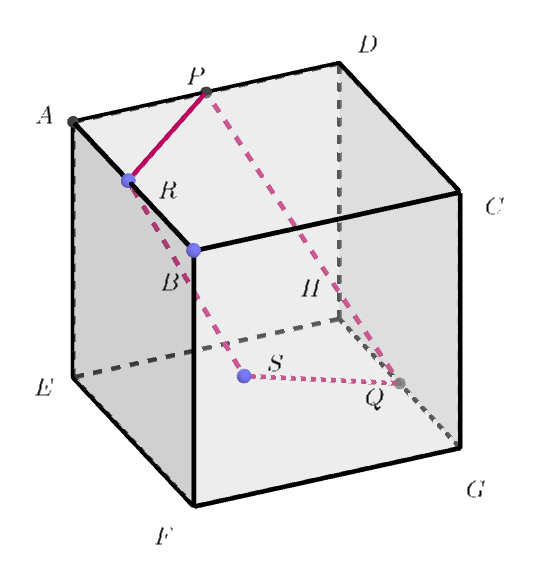
$立方体 \ ABCD-EFGH\ を考える。辺AD,\ GH\ の中点をそれぞれ、P,\ Q\ とする。辺AB\ を \ t:(1-t)\ に$
$内分する点を \ R\ とする \ \ (ただし、0 < t < 1)。\vec{AB}=\vec{a},\ \vec{AD}=\vec{b},\ \vec{AE}=\vec{c}\ \ と表す。いま、4\ 点 \ B,\ C,\ G,\ F\ を$
$通る平面上に点S\ をとり、\vec{AS}=\alpha \vec{a}+\beta \vec{b}+ \gamma \vec{c}\ \ (\alpha,\ \beta ,\ \gamma \ は実数)\ \ と表す。次の問いに答えよ。$
$\hspace{5em}$

$(1)\ \ \alpha \ を求めよ。また、\vec{AP},\ \ \vec{AQ},\ \ \vec{AR}\ \ をそれぞれ \ \vec{a},\ \vec{b},\ \vec{c},\ t\ を用いて表せ。$
$以降 \ P,\ Q,\ R,\ S\ が同一平面上にあるとする。$
$(2)\ \ \beta \ を \ \gamma , \ \ t\ の式で表せ。$
$(3)\ \ 直線 \ PS\ と直線 \ QR\ が垂直に交わるとき、\beta,\ \ \gamma \ \ をそれぞれ \ t\ の式で表せ。$
$(4)\ \ 直線 \ PS\ と直線 \ QR\ が垂直に交わり、かつ点S\ が立方体の面 \ BCGF\ 上にあるとき、t\ のとりうる値の$
$\quad 範囲を求めよ。$
(1)

$\vec{BS}=p\vec{BC}+q\vec{BF}\ \ (p,\ q \ は実数)\ \ とおける。$
$\vec{BC}=\vec{AD},\quad \vec{BF}=\vec{AE} \ \ だから$
$\vec{AS}-\vec{AB}=p\vec{AD}+q\vec{AE}$
$\therefore \ \ \vec{AS}=\vec{AB}+p\vec{AD}+q\vec{AE}=\vec{a}+p\vec{b}+q\vec{c}$
$一方\ \ 題意より \quad \vec{AS}=\alpha \vec{a}+\beta \vec{b}+ \gamma \vec{c}$
$\vec{a},\ \ \vec{b},\ \ \vec{c} \ \ は互いに平行でなく、同一平面上にないから \ \ (一次独立だから)$
$\alpha =1,\quad p=\beta,\quad q=\gamma$
$また$
$\vec{AP}=\dfrac{1}{2}\vec{AD}=\dfrac{1}{2}\vec{b}$
$\vec{AQ}=\vec{AH}+\vec{HQ}=(\vec{b}+\vec{c})+\dfrac{1}{2}\vec{a}=\dfrac{1}{2}\vec{a}+ \vec{b}+\vec{c}$
$\vec{AR}=t\vec{a}$
(2)
$\vec{PS}=k\vec{PQ}+\ell \vec{PR}\ \ (k,\ \ell \ \ は実数)\ \ とおける。$
$\vec{AS}-\vec{AP}=k(\vec{AQ}-\vec{AP}+\ell (\vec{AR}-\vec{AP})$
\begin{eqnarray*} \vec{AS} &=&(1-k- \ell )\vec{AP} +k\vec{AQ}+ \ell\vec{AR}\\ \\ &=&(1-k- \ell ) \times \dfrac{1}{2}\vec{b} +k \times (\dfrac{1}{2}\vec{a}+ \vec{b}+\vec{c}) + \ell \times t\vec{a}\\ \\ &=&(\dfrac{k}{2} + \ell t)\vec{a}+ \dfrac{1}{2}(1+k- \ell )\vec{b}+ k\vec{c}\\ \end{eqnarray*} $(1)より \quad \vec{AS}=\vec{a}+\beta \vec{b}+ \gamma \vec{c}\ \ だから$
\[ \hspace{1em} \left\{ \begin{array}{l} \dfrac{k}{2} + \ell t =1 \hspace{8em}①\\ \dfrac{1}{2}(1+k- \ell )=\beta \hspace{5.3em}②\\ k=\gamma \hspace{10.5em}③\\ \end{array} \right. \]
$③を①、②に代入して$
\[ \hspace{1em} \left\{ \begin{array}{l} \dfrac{\gamma}{2} + \ell t =1 \hspace{8.5em}④\\ 1 + \gamma - \ell =2\beta \hspace{7em}⑤\\ \end{array} \right. \]
$⑤より \quad \ell =1-2\beta + \gamma $
$これを④に代入して$
$\dfrac{\gamma}{2} + (1-2\beta + \gamma)t=1 $
$2\beta t=t+\gamma t +\dfrac{\gamma}{2} -1=\dfrac{1}{2}(\gamma +2\gamma t+2t-2)$
$\therefore \ \ \beta =\dfrac{(2t+1)\gamma +2t-2}{4t}$
(3)
$PS\ \perp \ QR \quad ならば \quad \vec{PS} \cdot \vec{QR}=0$
$(\vec{AS} -\vec{AP}) \cdot (\vec{AR}-\vec{AQ})=0$
$(1) をつかって$
$(\vec{a} +\beta \vec{b}+\gamma \vec{c} -\dfrac{1}{2}\vec{b}) \cdot (t\vec{a} -\dfrac{1}{2}\vec{a} -\vec{b}-\vec{c})=0$
$\big(\vec{a} +(\beta -\dfrac{1}{2})\vec{b}+\gamma \vec{c}\big) \cdot \big((t - \dfrac{1}{2})\vec{a} -\vec{b}-\vec{c}\big)=0$
$ここで \quad \vec{a} \perp \vec{b} , \quad \vec{b} \perp \vec{c}, \quad \vec{c} \perp \vec{a} \quad だから \quad \vec{a} \cdot \vec{b}=0 , \quad \vec{b} \cdot \vec{c}=0, \quad \vec{c} \cdot \vec{a}=0 \quad をつかって上式を展開すると$
$(t-\dfrac{1}{2})|\vec{a}|^2-(\beta -\dfrac{1}{2})|\vec{b}|^2-\gamma|\vec{c}|^2=0$
$|\vec{a}|=|\vec{b}|=|\vec{c}| \quad だから$
$(t-\dfrac{1}{2})-(\beta -\dfrac{1}{2})-\gamma =0$
$\therefore\ \ \beta + \gamma=t $
$(2)より \beta =\dfrac{(2t+1)\gamma +2t-2}{4t} を代入して$
$\dfrac{(2t+1)\gamma +2t-2}{4t}+\gamma =t$
$(2t+1)\gamma +2t-2 +4t \gamma =4t^2$
$(6t+1)\gamma =4t^2-2t+2$
$\therefore \ \ \gamma =\dfrac{4t^2-2t+2}{6t+1}$
$\beta=t-\gamma=t-\dfrac{4t^2-2t+2}{6t+1}=\dfrac{2t^2+3t-2}{6t+1}$
(4)
$問題文より \quad 0 < t < 1 \quad に注意して$
$直線 \ PS\ と直線 \ QR\ が垂直に交わるから(3)より \quad \beta=\dfrac{2t^2+3t-2}{6t+1},\quad \gamma =\dfrac{4t^2-2t+2}{6t+1}$
$点S\ が立方体の面 \ BCGF\ 上にある条件は(1)より \quad \vec{BS}=\beta \vec{BC}+ \gamma \vec{BF} \ \ において \quad 0 \leqq \beta \leqq 1, \quad 0 \leqq \gamma \leqq 1$
(i)$\ \ 0 \leqq \beta \leqq 1 \quad より \quad 0 \leqq \dfrac{2t^2+3t-2}{6t+1} \leqq 1$
$\qquad 6t+1 >0 \ \ だから \quad 0 \leqq 2t^2+3t-2 \leqq 6t+1$
$\quad (ア)\quad 2t^2+3t-2 \geqq 0 \ \ の解は$
$\qquad (2t-1)(t+2) \geqq 0$
$\qquad t+2 > 0 \ \ だから \ \ 2t-1 \geqq 0 \quad \therefore \ \ t \geqq \dfrac{1}{2}$
$\quad (イ) \quad 2t^2+3t-2 \leqq 6t+1 \ \ の解は$
$\qquad 2t^2-3t-3 \leqq 0$
$\qquad 2t^2-3t-3 =0 \ \ の解は \quad t=\dfrac{3 \pm \sqrt{33}}{4} \ \ だから \quad \dfrac{3-\sqrt{33}}{4} \leqq t \leqq \dfrac{3+\sqrt{33}}{4}$
$\qquad \dfrac{3-\sqrt{33}}{4} < 0,\quad \dfrac{3+\sqrt{33}}{4} > 1 \quad だから \quad 0 < t < 1$
$\quad (ア),(イ)まとめて \quad \dfrac{1}{2} \leqq t < 1$
(ii)$\ \ 0 \leqq \gamma \leqq 1 より \quad 0 \leqq \dfrac{4t^2-2t+2}{6t+1} \leqq 1$
$\qquad 6t+1 >0 \ \ だから \quad 0 \leqq 4t^2-2t+2 \leqq 6t+1$
$\quad (ア) \quad 4t^2-2t+2 \geqq 0 \ \ の解は$
$\qquad 2t^2-t+1 \geqq 0$
$\qquad 2t^2-t+1=2(t-\dfrac{1}{4})^2+\dfrac{7}{8} > 0 \ \ だから \quad 0 < t < 1 \ \ のすべての実数$
$\quad (イ) \quad 4t^2-2t+2 \leqq 6t+1 \ \ の解は$
$\qquad 4t^2-8t+1 \leqq 0$
$\qquad 4t^2-8t+1 =0 \ \ の解は \quad t=\dfrac{2 \pm \sqrt{3}}{2} \quad だから \quad \dfrac{2 - \sqrt{3}}{2} \leqq t \leqq \dfrac{2 + \sqrt{3}}{2} $
$\qquad 0 < \dfrac{2 -\sqrt{3}}{2} < 1 < \dfrac{2 + \sqrt{3}}{2} \quad だから \quad \dfrac{2 -\sqrt{3}}{2} \leqq t < 1$
$\quad (ア),(イ)まとめて \quad \dfrac{2-\sqrt{3}}{2} \leqq t < 1$
(i),(ii)$ まとめて \qquad \dfrac{2-\sqrt{3}}{2} < \dfrac{1}{2} \quad だから \quad \dfrac{1}{2} \leqq t < 1$
メインメニュー に戻る