横浜国立大学(理系) 2024年 問題5
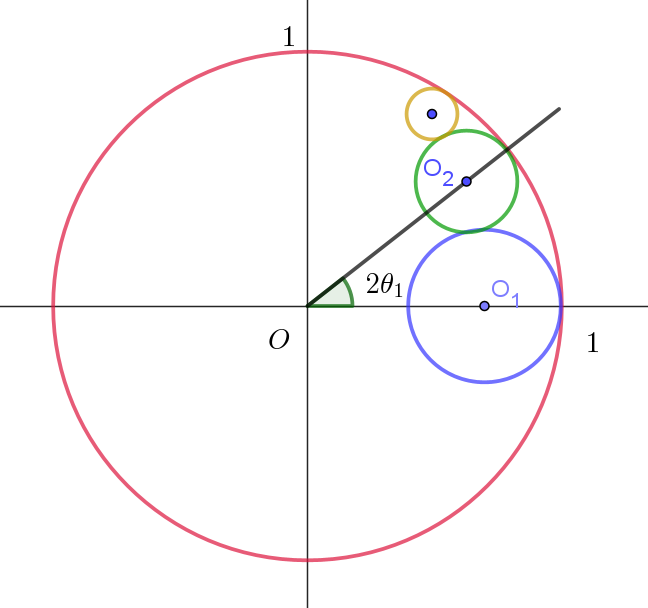
$xy\ 平面上に、原点 \ O\ を中心とする半径 \ 1\ の円 \ C\ がある。さらに、n=1,\ 2,\ 3,\ \cdots \ に対して、中心 \ O_n,$
$半径 \ r_n \ の円 \ C_n \ があり、以下の$(i),(ii),(iii)$をみたす。$
(i)$\ \ 点O_1\ の座標は(1-r_1,\ 0)\ であり、かつ \ \ r_1 < 1 \ \ である。$
(ii)$\ \ n=1,\ 2,\ 3,\ \cdots \ \ に対して、C_{n+1} \ は \ C\ に内接し、C_{n+1}\ と \ C_n \ は外接する。$
(iii)$\ \ n=1,\ 2,\ 3,\ \cdots \ に対して、半直線 \ OO_{n+1} \ は、O\ を中心として半直線 \ OO_n \ を時計の針の回転と$
$\hspace{3em} 逆向きに \ 2\theta_n \ 回転したものであり、0 < 2\theta_n < \pi \ \ である。$
$\hspace{20em}$
$次の問いに答えよ。$
$(1)\ \ \sin ^2\theta_1\ \ を \ r_1,\ r_2\ の式で表せ。$
$以下、r_n=\dfrac{1}{2^{n+1}+1} \ \ (n=1,\ 2,\ 3,\ \cdots )\ \ とする。$
$(2)\ \ n=1,\ 2,\ 3,\ \cdots \ に対して、\sin \theta_n \ \ を \ n\ の式で表せ。$
$(3)\ \ 0 < x < \dfrac{\pi}{6}\ \ に対して、 \sin x < x < \sin x + \dfrac{1}{5}\sin ^3x \ \ を示せ。$
$\quad 必要ならば、3.14 < \pi < 3.15 \ \ を用いてよい。$
\[(4)\ \ 極限値 \ \ \lim_{n \rightarrow \infty} \sum_{k=1}^n \theta _k \ \ は存在し、その極限値を \ \alpha \ とおく。\alpha \ の小数第 \ 2\ 位まで\ (小数第 \ 3\ 位切り捨て)\]
$\quad を求めよ。必要ならば、1.41 < \sqrt{2}< 1.42 \ \ を用いてよい。$
(1)
$\triangle OO_1O_2 \ \ において \quad OO_1=1-r_1,\quad OO_2=1-r_2,\quad O_1O_2=r_1+r_2 \quad だから余弦定理を用いて$
$\cos 2\theta_1=\cfrac{OO1^2+OO_2^2-O_1O_2^2}{2OO_1\cdot OO_2}=\cfrac{(1-r_1)^2+(1-r_2)^2-(r_1+r_2)^2}{2(1-r_1)(1-r_2)}=\cfrac{1-r_1-r_1-r_1r_2}{(1-r_1)(1-r_2)}$
$1-2\sin ^2\theta_1 =\cfrac{1-r_1-r_1-r_1r_2}{(1-r_1)(1-r_2)}$
$2\sin ^2\theta_1 =1-\cfrac{1-r_1-r_1-r_1r_2}{(1-r_1)(1-r_2)}=\cfrac{(1-r_1)(1-r_2)-(1-r_1-r_1-r_1r_2)}{(1-r_1)(1-r_2)}=\cfrac{2r_1r_2}{(1-r_1)(1-r_2)}$
$\therefore \ \ \sin ^2\theta_1 =\cfrac{r_1r_2}{(1-r_1)(1-r_2)}$
(2)
$\triangle OO_nO_{n+1} \ \ において \quad OO_n=1-r_n, \quad OO_{n+1}=1-r_{n+1}, \quad O_nO_{n+1}=r_n+r_{n+1} \quad だから(1)と同様にして$
$\sin ^2\theta_n =\cfrac{r_nr_{n+1}}{(1-r_n)(1-r_{n+1})}$
$r_n=\dfrac{1}{2^{n+1}+1} \ \ (n=1,\ 2,\ 3,\ \cdots )\ \ だから$
$\sin ^2\theta_n=\cfrac{\dfrac{1}{2^{n+1}+1} \times \dfrac{1}{2^{n+2}+1}}{\big(1-\dfrac{1}{2^{n+1}+1} \big)\big(1-\dfrac{1}{2^{n+2}+1}\big)}=\cfrac{1}{2^{n+1} \times 2^{n+2}}=\cfrac{1}{2^{2n+3}}$
$\therefore \ \ \sin \theta_n=\cfrac{1}{2\sqrt{2}\cdot 2^n}$
(3)
(i)$\ \ \sin x < x \quad の証明$
$\quad f(x)=x-\sin x \quad とおくと$
$\quad f'(x)=1-\cos x > 0 \quad よって \ \ f(x) \ は単調増加$
$\quad f(x) > f(0)=0 \quad したがって \quad \sin x < x$
(ii)$\ \ x < \sin x + \cfrac{1}{5}\sin ^3 x \quad の証明$
$\quad g(x)=\sin x +\cfrac{1}{5}\sin ^3 x -x \quad とおくと$
\begin{eqnarray*} \quad g'(x) &=&\cos x +\cfrac{3}{5}\sin ^2x \cos x -1\\ \\ &=&\cos x +\cfrac{3}{5}(1-\cos ^2x)\cos x -1\\ \\ &=&\cfrac{8}{5}\cos x - \cfrac{3}{5}\cos ^3x -1\\ \end{eqnarray*} $\quad \cos x =t \quad とおくと \quad 0 < x < \dfrac{\pi}{6} \quad より \quad \cfrac{\sqrt{3}}{2} < t < 1$
$\quad g'(x)=h(t) \quad とおくと$
$\quad h(t)=\cfrac{8}{5}t - \cfrac{3}{5}t^3 -1$
$\quad h'(t)=\cfrac{8}{5}-\cfrac{9}{5}t^2=-\cfrac{9}{5}(t^2-\cfrac{8}{9})$
$\quad h'(t)=0 \quad より \quad t=\cfrac{2\sqrt{2}}{3}$
$\quad \cfrac{\sqrt{3}}{2} < \cfrac{2\sqrt{2}}{3} < 1 \quad だから$
$増減表$
\begin{array}{c||c|c|c|c|c} t& \dfrac{\sqrt{3}}{2} & \cdots & \dfrac{2\sqrt{2}}{3} & \cdots & 1\\ \hline h'(t)& & + & 0 & - & \\ \hline h(t)& - & \nearrow & 極大 & \searrow & 0 \\ \end{array}
$\quad h(\dfrac{\sqrt{3}}{2})=\cfrac{8}{5} \times \cfrac{\sqrt{3}}{2} - \cfrac{3}{5} \times \cfrac{3\sqrt{3}}{8}-1=\cfrac{23\sqrt{3}-40}{40}<0 \qquad (23^2 \times 3 < 40^2 \ \ より)$
$\quad h(1)=\cfrac{8}{5} - \cfrac{3}{5} -1=0$
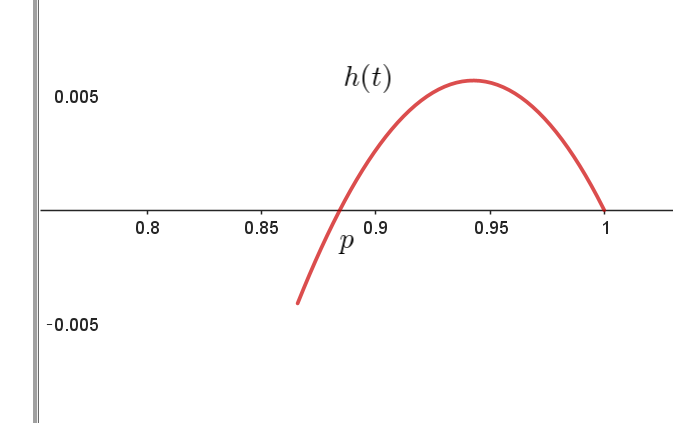
$\quad したがって \quad h(\dfrac{2\sqrt{2}}{3}) > 0$
$\quad h(t) \ は連続で、\dfrac{\sqrt{3}}{2} < t < \dfrac{2\sqrt{2}}{3} \ \ で単調増加だから$
$\quad 中間値の定理より \ \ h(p)=0\ \ となる \ p \ が区間 (\dfrac{\sqrt{3}}{2},\ \dfrac{2\sqrt{2}}{3})\ に$
$\quad 1\ つだけ存在する。$
$\quad \dfrac{\sqrt{3}}{2} < t < p \ \ で \ \ h(t) < 0,\qquad p < t < 1 \ \ で \ \ h(t) > 0$
$\quad よって$
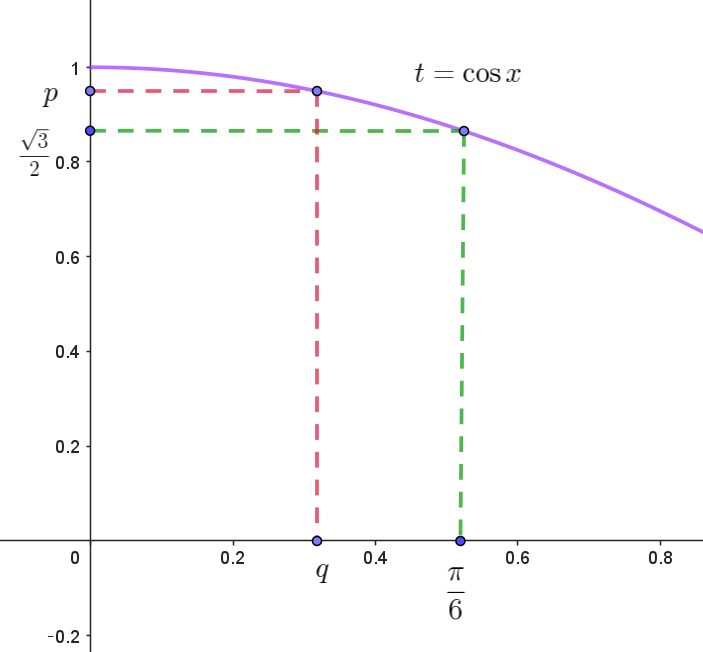
$\quad \dfrac{\sqrt{3}}{2} < \cos x < p \ \ で \ \ g'(x) < 0,\qquad p < \cos x < 1 \ \ で \ \ g'(x) > 0$
$\quad \cos q =p \quad とおくと$
$\quad q < x < \cfrac{\pi}{6}\ \ で \ \ g'(x) < 0,\qquad 0 < x < q \ \ で \ \ g'(x) > 0$
$増減表$
\begin{array}{c||c|c|c|c|c}
x & 0 & \cdots & q & \cdots & \dfrac{\pi}{6}\\
\hline
g'(x) & & + & 0 & - & \\
\hline
g(x) & 0 & \nearrow & 極大 & \searrow & + \\
\end{array}
$\quad g(0)=0$
$\quad g(\dfrac{\pi}{6})=\cfrac{1}{2}+\cfrac{1}{5} \times \cfrac{1}{8}-\cfrac{\pi}{6}=\cfrac{64-20\pi}{120} > \cfrac{64-20 \times 3.15}{120} > 0$
$\quad よって \quad g(x) > 0 \quad だから \quad x < \sin x + \dfrac{1}{5}\sin ^3x $
(i),(ii)$より \quad 0 < x < \dfrac{\pi}{6}\ \ に対して、 \sin x < x < \sin x + \dfrac{1}{5}\sin ^3x \quad が成りたつ$
(4)
$\sin \theta_n=\cfrac{1}{2\sqrt{2}\cdot 2^n} < \cfrac{1}{2\sqrt{2}\cdot 2} < \cfrac{1}{2}$
$\therefore\ \ 0 < \theta_n < \cfrac{\pi}{6}$
$よって (3) がつかえて$
$\sin \theta_n < \theta_n < \sin \theta_n + \dfrac{1}{5}\sin ^3 \theta_n $
$(2)より \quad \cfrac{1}{2\sqrt{2}\cdot 2^n} < \theta_n < \cfrac{1}{2\sqrt{2}\cdot 2^n } + \cfrac{1}{5} \times \big(\cfrac{1}{2\sqrt{2}\cdot 2^n}\big)^3$
\[\lim_{n \rightarrow \infty} \sum_{k=1}^n \cfrac{1}{2\sqrt{2}\cdot 2^k}=\lim_{n \rightarrow \infty} \cfrac{1}{2\sqrt{2}} \sum_{k=1}^n \cfrac{1}{2^k}= \cfrac{1}{2\sqrt{2}} \times \cfrac{\dfrac{1}{2}}{1-\dfrac{1}{2}}=\cfrac{\sqrt{2}}{4} \]
\[\lim_{n \rightarrow \infty} \sum_{k=1}^n \big(\cfrac{1}{2\sqrt{2}\cdot 2^k}\big)^3=\lim_{n \rightarrow \infty} \cfrac{1}{16\sqrt{2}} \sum_{k=1}^n \cfrac{1}{8^k}= \cfrac{1}{16\sqrt{2}} \times \cfrac{\dfrac{1}{8}}{1-\dfrac{1}{8}}=\cfrac{\sqrt{2}}{224} \]
$したがって$
$\cfrac{\sqrt{2}}{4}< \alpha < \cfrac{\sqrt{2}}{4} + \cfrac{1}{5} \times \cfrac{\sqrt{2}}{224}$
$ここで \quad \cfrac{1}{5} \times \cfrac{\sqrt{2}}{224}=\cfrac{\sqrt{2}}{1120}< \cfrac{\sqrt{2}}{1000} < 0.00142 \quad だからこの項は無視してよい。$
$\cfrac{1.41}{4} < \alpha < \cfrac{1.42}{4}$
$0.3525 < \alpha < 0.3550$
$小数第 \ 2\ 位までとって \quad \alpha= 0.35$
メインメニュー に戻る