横浜国立大学(理系) 2024年 問題4
$\alpha \ を、|\alpha| < 1\ \ をみたす複素数とする。\overline{\alpha}z \ne 1 \ \ となる複素数 \ z\ に対して、w=\cfrac{\alpha -z}{1-\overline{\alpha}z} \ \ と定める。$
$ただし、\overline{\alpha} \ は \ \alpha \ の共役複素数を表す。次の問いに答えよ。$
$(1)\ \ z\ が \ |z|=\dfrac{1}{3}\ をみたしながら動くとき、w\ の描く図形 \ D\ を求め、\alpha =\dfrac{1}{2}\ のとき、D\ を複素数平面に$
$\quad 図示せよ。$
$(2)\ \ \alpha \ が \ |\alpha|=\dfrac{1}{2}\ をみたしながら動くとき、(1)で求めた図形 \ D\ が通過する範囲 \ E\ を求め、E\ を複素数$
$\quad平面に図示せよ。$
(1)
$w=\cfrac{\alpha -z}{1-\overline{\alpha}z} \quad より \quad w(1-\overline{\alpha}z)=\alpha - z$
$z(\overline{\alpha}w-1)=w- \alpha $
$|z|=\cfrac{1}{3} \quad より \quad \cfrac{1}{3}|\overline{\alpha}w-1|=|w-\alpha|$
$3|w-\alpha |=|\overline{\alpha}w-1|$
$3|w-\alpha |=|\overline{\alpha}|\big|w-\dfrac{1}{\overline{\alpha}}\big|$
$これは、w\ が \ 2\ 定点 \ \ \alpha, \ \ \dfrac{1}{\overline{\alpha}} \quad からの距離の比が \ \ 3:|\overline{\alpha}|\ \ (一定)\ \ であることを示しているから$
$w\ の描く図形Dは(アポロニウスの)円である。$
$この円の方程式を具体的に求めるには$
$9|w-\alpha |^2=|\overline{\alpha} w - 1|^2 \quad より$
$9(w-\alpha )(\overline{w}-\overline{\alpha})=(\overline{\alpha} w - 1)(\alpha \overline{w} - 1)$
$(9-|\alpha|^2)|w|^2-8\overline{\alpha}w - 8 \alpha \overline{w}=1-9|\alpha|^2$
$|w|^2-\cfrac{8\overline{\alpha}}{9-|\alpha|^2}w - \cfrac{8 \alpha}{9-|\alpha|^2} \overline{w}=\cfrac{1-9|\alpha|^2}{9-|\alpha|^2}$
$\big(w-\cfrac{8\alpha}{9-|\alpha|^2}\big) \big(\overline{w} - \cfrac{8 \overline{\alpha}}{9-|\alpha|^2}\big) =\cfrac{1-9|\alpha|^2}{9-|\alpha|^2}+ \cfrac{8\alpha}{9-|\alpha|^2} \times \cfrac{8\overline{\alpha}}{9-|\alpha|^2}$
$\big(w-\cfrac{8\alpha}{9-|\alpha|^2}\big) \big(\overline{w} - \cfrac{8 \overline{\alpha}}{9-|\alpha|^2}\big) =\cfrac{(1-9|\alpha|^2)(9-|\alpha|^2)+64|\alpha|^2}{(9-|\alpha|^2)^2}$
$\big(w-\cfrac{8\alpha}{9-|\alpha|^2}\big) \big(\overline{w} - \cfrac{8 \overline{\alpha}}{9-|\alpha|^2}\big) =\cfrac{9-18|\alpha|^2 + 9|\alpha|^4}{(9-|\alpha|^2)^2}$
$\big|w-\cfrac{8\alpha}{9-|\alpha|^2}\big|^2 =\cfrac{9(1-|\alpha|^2 )^2}{(9-|\alpha|^2)^2}$
$|\alpha| < 1 \quad だから \quad 1-|\alpha|^2 > 0, \quad 9-|\alpha|^2 > 0$
$\big|w-\cfrac{8\alpha}{9-|\alpha|^2}\big| =\cfrac{3(1-|\alpha|^2 )}{9-|\alpha|^2}$
$よって \ \ 図形 \ D\ は \quad 中心 \cfrac{8\alpha}{9-|\alpha|^2} , \quad 半径 \quad \cfrac{3(1-|\alpha|^2 )}{9-|\alpha|^2} \quad の円$
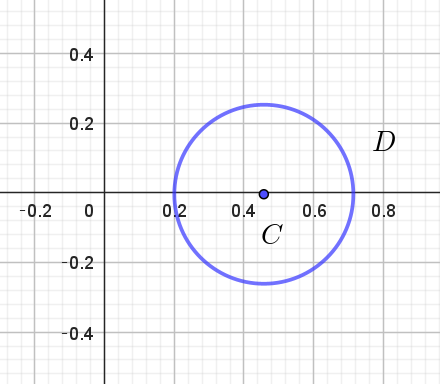
$とくに\quad \alpha =\cfrac{1}{2} \quad のとき \quad \big|w-\cfrac{16}{35}\big| =\cfrac{9}{35}\quad だから$
$図形 \ D\ は \quad 中心 \ C(\cfrac{16}{35}), \quad 半径 \ \ \cfrac{9}{35} \ \ の円である。$
$右図はこれを図示したものである。$
(2)
$(1)より図形 \ D\ は \quad \big|w-\cfrac{8\alpha}{9-|\alpha|^2}\big| =\cfrac{3(1-|\alpha|^2 )}{9-|\alpha|^2} \quad だから$
$|\alpha|=\cfrac{1}{2} \quad のとき$
$\big|w-\dfrac{8\alpha}{9-\dfrac{1}{4}}\big| =\cfrac{3(1-\dfrac{1}{4})}{9-\dfrac{1}{4}}$
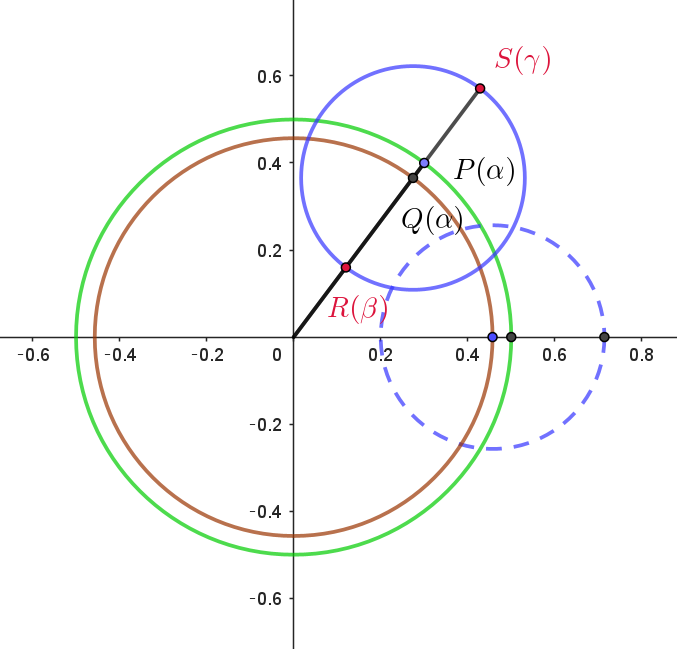
$\big|w-\dfrac{32}{35}\alpha\big| =\cfrac{9}{35}$
$よって \quad w\ は中心 \ \ (\dfrac{32}{35}\alpha),\quad 半径 \ \ \cfrac{9}{35} \ \ の円を描く。$
$右図は、|\alpha|=\cfrac{1}{2} \ \ 上の任意の点 \ P(\alpha) \ \ に対して、$
$w\ の中心 \ \ (\dfrac{32}{35}\alpha)\ を \ Q(\alpha)\ \ とおく。$
$線分 \ OQ\ と円 \ w\ の交点を \ R(\beta),\ \ S(\gamma) \ \ とおくと$
$図形 \ D\ が通過する範囲 \ E\ は点R(\beta),\ \ S(\gamma) \ \ の描く曲線(軌跡)である。$
$(1)より、とくに \ \ \alpha=\cfrac{1}{2} \ \ のとき$
$\beta=\cfrac{16}{35}-\cfrac{9}{35}=\cfrac{1}{5},\qquad \gamma=\cfrac{16}{35}+\cfrac{9}{35}=\cfrac{5}{7}$
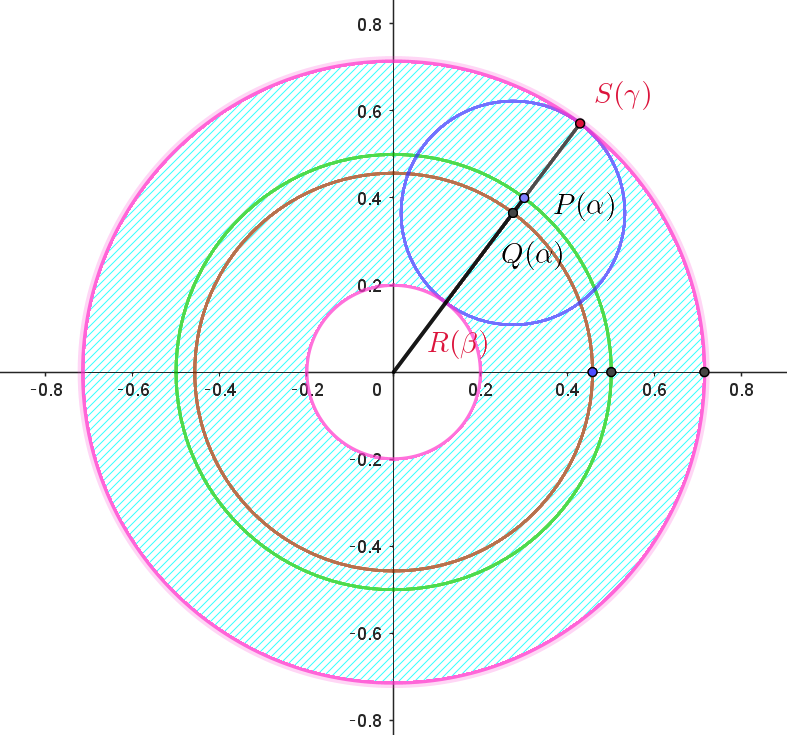
$よって$
$R(\beta)\ \ は原点中心、半径 \ \ \cfrac{1}{5}\ \ の円$
$S(\gamma) \ は原点中心、半径 \ \ \cfrac{5}{7}\ \ の円$
$を描く。複素数平面に図示した \ E\ は右図の青色で示した$
$ドーナツ状の領域である。$
$点R(\beta),\ \ S(\gamma) \ \ の軌跡をきちんと求めるには次のようにすればよい。$
$(別解)$
(i)$\ \ 点R(\beta)\ \ について$
$R(\beta)\ は円 \ w\ 上の点だから \quad \big|\beta -\dfrac{32}{35}\alpha\big| =\cfrac{9}{35} \hspace{5em}①$
$R(\beta),\ \ Q(\alpha),\ \ P(\alpha) \ \ は一直線上にあり、R(\beta)Q(\alpha)=\cfrac{9}{35},\ \ OP(\alpha)=\cfrac{1}{2} \quad だから$
$\cfrac{32}{35}\alpha -\beta=\cfrac{\dfrac{9}{35}}{\dfrac{1}{2}}\alpha$
$\cfrac{32}{35}\alpha -\beta=\cfrac{18}{35}\alpha$
$\alpha=\cfrac{35}{14}\beta$
$①に代入して$
$\big|\beta -\dfrac{32}{35} \times \cfrac{35}{14}\beta \big|=\cfrac{9}{35}$
$\big|\beta -\dfrac{16}{7} \beta \big|=\cfrac{9}{35}$
$\big|\dfrac{9}{7} \beta \big|=\cfrac{9}{35}$
$|\beta |=\cfrac{1}{5}$
$よって \quad R(\beta) \ は原点中心、半径 \ \ \cfrac{1}{5}\ \ の円を描く。$
(ii)$\ \ 点S(\gamma) \ \ について$
$S(\gamma)\ は円 \ w\ 上の点だから \quad \big|\gamma -\dfrac{32}{35}\alpha\big| =\cfrac{9}{35} \hspace{8em}②$
$R(\beta)\ と \ S(\gamma) \ の中点は \ Q(\alpha)\ \ だから \quad \cfrac{\beta + \gamma}{2}=\cfrac{32}{35}\alpha \hspace{5em}③$
$\alpha=\cfrac{35}{14}\beta \quad より \quad \beta =\cfrac{14}{35}\alpha$
$③に代入して$
$\cfrac{14}{35}\alpha + \gamma =\cfrac{64}{35}\alpha $
$\gamma=\cfrac{50}{35}\alpha =\cfrac{10}{7}\alpha$
$\alpha=\cfrac{7}{10}\gamma$
$②に代入して$
$\big|\gamma -\dfrac{32}{35} \times \cfrac{7}{10}\gamma \big|=\cfrac{9}{35}$
$\big|\gamma -\dfrac{16}{25} \gamma \big|=\cfrac{9}{35}$
$\big|\dfrac{9}{25} \gamma \big|=\cfrac{9}{35}$
$|\gamma |=\cfrac{5}{7}$
$よって \quad S(\gamma) \ \ は原点中心、半径 \ \ \cfrac{5}{7}\ \ の円を描く。$
メインメニュー に戻る