MY MATH NOTE

横浜国立大学(理系) 2024年　問題2

$1\ 辺の長さが \ 1\ の正六角形 \ A_1A_2A_3A_4A_5A_6\ がある。$
$\hspace{20em}$ 　
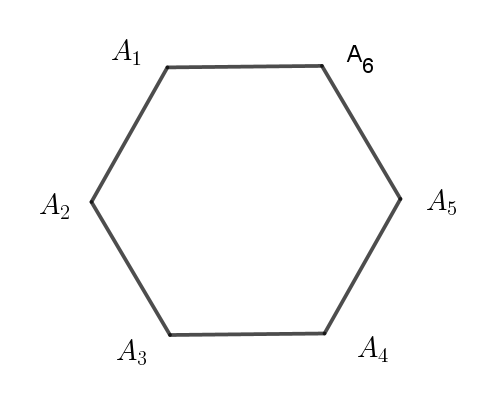
$1\ 個のさいころを続けて \ 5\ 回投げ、出た目を順に \ n_1,\ n_2,\ n_3,\ n_4,\ n_5,\ n_6\ とおく。次の条件付き確率を$
$それぞれ求めよ。$
$(1)\ \ 「n_1,\ n_2,\ n_3\ がすべて異なる」という条件のもとで、「三角形 \ A_{n_1} A_{n_2} A_{n_3}\ の面積が \ \dfrac{\sqrt{3}}{2}\ である」$
$\quad という条件付き確率$
$(2)\ \ 「n_1,\ n_2,\ n_3 \ がすべて異なり、かつ、n_4 \ne n_5 \ である」という条件のもとで、「線分 \ A_{n_4}A_{n_5}\ が$
$\quad 三角形 \ A_{n_1}A_{n_2}A_{n_3}\ の面積を \ 2\ 等分する」という条件付き確率$

(1)

　
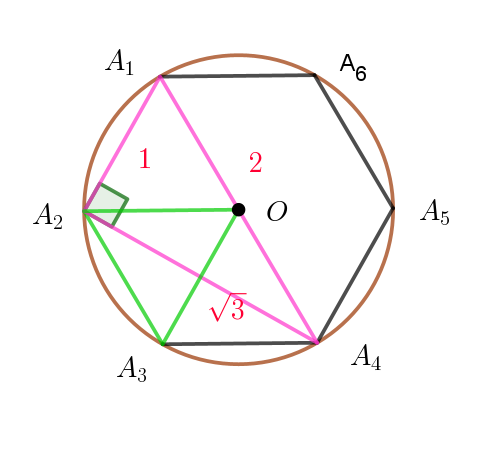
$右図で、\angle OA_1A_2=60°、\angle OA_2A_4=30°\quad だから$

$\angle A_1A_2A_4=90°$

$あるいは、点A_1～A_6\ は点 \ O\ を中心、半径 \ 1\ の円周上にあるから、$

$円周角の定理で求めることもできる。$

$\triangle A_1A_2A_4 \quad において \quad A_1A_2=1,\ \ A_1A_4=2 \ \ だから \ \ A_2A_4=\sqrt{2^2-1^2}=\sqrt{3}$

$したがって \quad \triangle A_1A_2A_4=\cfrac{\sqrt{3}}{2}$

$今後、\triangle A_1A_2A_4 \ を単に\ (1\ 2\ 4)\ と表すことにする。$

$直角三角形 \ A_1A_2A_4 \ と合同な三角形はこれを含めて$

$(1\ 2\ 4),\ \ (1\ 2\ 5),\ \ (2\ 3\ 5),\ \ (2\ 3\ 6),\ \ (3\ 4\ 6),\ \ (3\ 4\ 1),\ \ (4\ 5\ 1),\ \ (4\ 5\ 2),\ \ (5\ 6\ 2),\ \ (5\ 6\ 3),\ \ (6\ 1\ 3),\ \ (6\ 1\ 4)$

$の\ 12\ 個ある。$

$三角形 \ A_1A_2A_4 \ が作られるのは、さいころの出た目が$

$(n_1,\ n_2,\ n_3)=(1,\ 2,\ 4)\ \ 以外に \ \ (1,\ 4,\ 2),(2,\ 1,\ 4),(2,\ 4,\ 1),(4,\ 1,\ 2),(4,\ 2,\ 1)\ \ の \ \ 3!\ 通りある。$

$したがって 三角形 \ A_{n_1} A_{n_2} A_{n_3}\ の面積が \ \dfrac{\sqrt{3}}{2}\ である事象Aの根元事象の個数 \ n(A)\ は$

$n(A)=12 \times 3! \ \ 通り$

$n_1,\ n_2,\ n_3\ がすべて異なる事象の個数 \ N\ は \quad N={}_6P_3=6 \times 5 \times 4 \ \ 通り$

$よって、n_1,\ n_2,\ n_3\ がすべて異なるという条件のもとで、三角形 \ A_{n_1} A_{n_2} A_{n_3}\ の面積が \ \dfrac{\sqrt{3}}{2}\ である$

$条件付き確率は \quad P=\cfrac{n(A)}{N}=\cfrac{12 \times 3!}{6 \times 5 \times 4}=\cfrac{3}{5}$

(2)

　
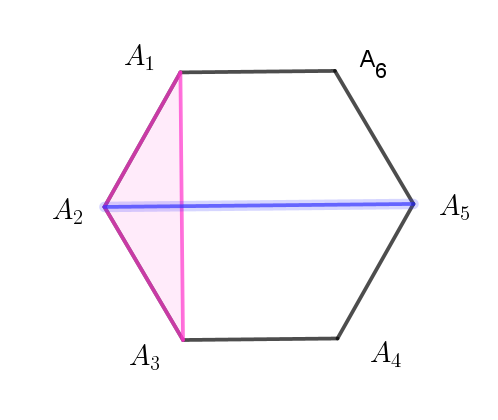
$図 \ 1\ は、二等辺三角形\ A_1A_2 A_3 \ を線分 \ A_2A_5 \ が \ 2\ 等分する場合で、合同な三角形と$

$線分はこれを含めて$

$(1\ 2\ 3)(2\ 5),\ \ (2\ 3\ 4)(3\ 6),\ \ (3\ 4\ 5)(4\ 1),\ \ (4\ 5\ 6)(5\ 2),\ \ (5\ 6\ 1)(6\ 3),\ \ (6\ 1\ 2)(1\ 4)$

$の \ 6\ 個ある。$

$二等辺三角形\ A_1A_2 A_3 と線分 \ A_2A_5 \ が作られるのは、さいころの出た目が \ \ 3! \times 2 \ \ 通りあるから$

$図 \ 1\ の場合は、6 \times 3! \times 2=72 \ \ 通り$
$\hspace{45em}図 \ 2$

　
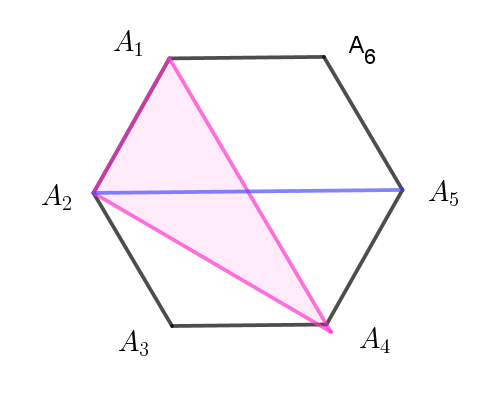
$図 \ 2\ は、三角形\ A_1A_2 A_4 を線分 \ A_2A_5 \ が \ 2\ 等分する場合で、合同な三角形と線分は$

$これを含めて$

$(1\ 2\ 4)(2\ 5),\ \ (2\ 3\ 5)(3\ 6),\ \ (3\ 4\ 6)(4\ 1),\ \ (4\ 5\ 1)(5\ 2),\ \ (5\ 6\ 2)(6\ 3),\ \ (6\ 1\ 3)(1\ 4)$

$の \ 6\ 個ある。$

$二等辺三角形\ A_1A_2 A_4 \ と線分 \ A_2A_5 \ が作られるのは、さいころの出た目が \ \ 3! \times 2 \ \ 通りあるから$

$図 \ 2\ の場合は、6 \times 3! \times 2=72 \ \ 通り$
$\hspace{45em}図 \ 3$

　
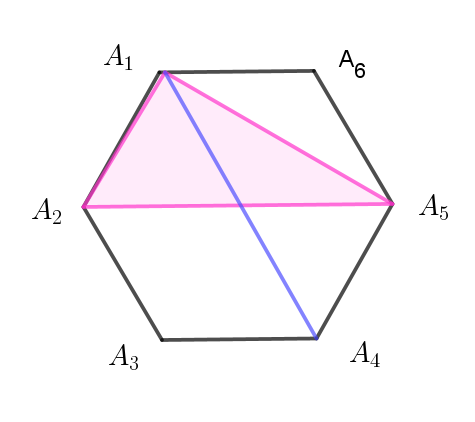
$図 \ 3\ は$

$直角三角形\ A_1A_2 A_5 を線分 \ A_1A_4 \ が2\ 等分する場合で、合同な三角形と線分は$

$これを含めて$

$(1\ 2\ 5)(1\ 4),\ \ (2\ 3\ 6)(2\ 5),\ \ (3\ 4\ 1)(3\ 6),\ \ (4\ 5\ 2)(4\ 1),\ \ (5\ 6\ 3)(5\ 2),\ \ (6\ 1\ 4)(6\ 3)$

$の \ 6\ 個ある。$

$直角三角形\ A_1A_2 A_4 と線分 \ A_2A_5 \ が作られるのは、さいころの出た目が \ \ 3! \times 2 \ \ 通りあるから$

$図 \ 3\ の場合は、6 \times 3! \times 2=72 \ \ 通り$
$\hspace{45em}図\ 4$

　
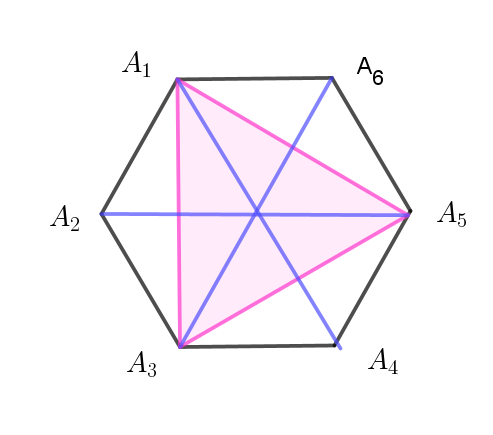
$図 \ 4\ は$

$正三角形\ A_1A_3 A_5 \ \ を線分 \ A_1A_4 、\ \ A_2A_5 、\ \ A_3A_6 \ \ が2\ 等分する場合で$

$(1\ 3\ 5)(1\ 4),\ \ (1\ 3\ 5)(2\ 5),\ \ (1\ 3\ 5)(3\ 6)$

$これと合同な三角形と線分は$

$正三角形 \ A_2A_4 A_6 \ \ を線分 \ A_2A_5 、\ \ A_3A_6 、\ \ A_4A_1 \ \ が2\ 等分する場合で$

$(2\ 4\ 6)(2\ 5),\ \ (2\ 4\ 6)(3\ 6),\ \ (2\ 4\ 6)(4\ 1)$

$正三角形\ A_1A_2 A_4 と線分 \ A_2A_5 \ が作られるのは、さいころの出た目が \ \ 3! \times 2 \ \ 通りあるから$

$図 \ 4の場合は、 2 \times 3! \times 2 \times 3=72 \ \ 通り$


$n_1,\ n_2,\ n_3\ がすべて異なり、n_4 \ne n_5 である事象の個数 \ N\ は \ \ N={}_6P_3 \times {}_6P_2 \ \ 通り$

$よって、n_1,\ n_2,\ n_3 \ がすべて異なり、かつ、n_4 \ne n_5 \ であるという条件のもとで、線分 \ A_{n_4}A_{n_5}\ が$

$三角形 \ A_{n_1}A_{n_2}A_{n_3}\ の面積を \ 2\ 等分するという条件付き確率は$

$P=\cfrac{n(A)}{N}=\cfrac{72 \times 4}{6 \times 5 \times 4 \times 6 \times 5}=\cfrac{2}{25}$

ページの先頭へ↑