$n\ を正の整数とする。xy\ 平面において、以下の \ 2\ つの曲線 \ C_1,\ C_2\ を考える。$
$\qquad C_1: y=(\cos x)^n \ \ (0 \leqq x \leqq \cfrac{\pi}{2}) \qquad C_2: y=(\sin x)^n \ \ (0 \leqq x \leqq \cfrac{\pi}{2}) $
$次の問いに答えよ。$
$(1)\ \ C_1\ と \ C_2\ の交点の座標を求めよ。$
$(2)\ \ n=4 \ のとき、C_1,\ C_2\ と \ y\ 軸で囲まれる部分の面積を求めよ。$
$(3)\ \ n=8 \ のとき、C_1,\ C_2\ と \ y\ 軸で囲まれる部分の面積を求めよ。$
(1)
$以下 \ \ (\cos x)^n ,\ \ (\sin x)^n \ を単に \ \ \cos ^n x ,\ \ \sin ^n x \ \ と書くことにする。$
$\cos ^n x =\sin ^n x \ \ において \ \ \cos x=0\ \ をみたす \ x\ は \ \ x=\cfrac{\pi}{2} \quad このとき \ \ \sin x=1 \ \ だから \ \ \cos x \ne 0$
$両辺を \ \ \cos ^n x \ \ で割って \quad \cfrac{\sin ^n x}{\cos ^n x}=1 \qquad \tan ^n x=1$
$一般に \ \ x^n-1=0 \ \ の正の実数解は$
$\quad (x-1)(x^{n-1}+x^{n-2}+ \cdots +x+1)=0 \quad より \ \ x=1\ \ のみだから$
$\tan x=1 \quad 0 \leqq x \leqq \cfrac{\pi}{2} \quad より \quad x=\cfrac{\pi}{4}$
$このとき \quad y=\cos ^n \cfrac{\pi}{4}=\big(\cfrac{1}{\sqrt{2}})^n=2^{-\scriptsize{\cfrac{n}{2}}}$
$交点の座標は \ \ \big(\cfrac{\pi}{4},\ 2^{-\scriptsize{\cfrac{n}{2}}}\big)$
(2)
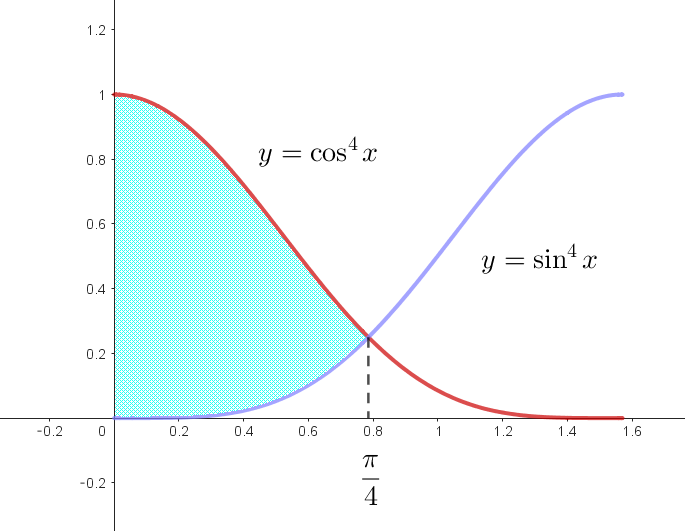
\begin{eqnarray*}
S_4
&=&\int_0^{\scriptsize{\cfrac{\pi}{4}}}(\cos ^4 x -\sin ^4 x)dx\\
\\
&=&\int_0^{\scriptsize{\cfrac{\pi}{4}}}(\cos ^2 x -\sin ^2 x) (\cos ^2 x +\sin ^2 x)dx\\
\\
&=&\int_0^{\scriptsize{\cfrac{\pi}{4}}}(\cos ^2 x -\sin ^2 x)dx\\
\\
&=&\int_0^{\scriptsize{\cfrac{\pi}{4}}}\cos 2xdx\\
\\
&=&\cfrac{1}{2}\big[\sin 2x \big]_0^{\scriptsize{\cfrac{\pi}{4}}}\\
\\
&=&\cfrac{1}{2}\sin \cfrac{\pi}{2}\\
\\
&=&\cfrac{1}{2}
\end{eqnarray*}
(3)
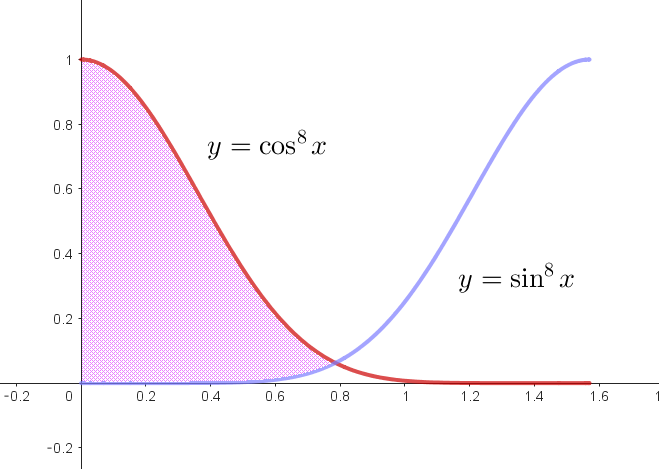
\begin{eqnarray*}
S_8
&=&\int_0^{\scriptsize{\cfrac{\pi}{4}}}(\cos ^8 x -\sin ^8 x)dx\\
\\
&=&\int_0^{\scriptsize{\cfrac{\pi}{4}}}(\cos ^4 x - \sin ^2 x) (\cos ^4 x + \sin ^ 4 x)dx\\
\\
&=&\int_0^{\scriptsize{\cfrac{\pi}{4}}}(\cos ^2 x -\sin ^2 x)(\cos ^2 x + \sin ^2 x) (\cos ^4 x + \sin ^ 4 x)dx\\
\\
&=&\int_0^{\scriptsize{\cfrac{\pi}{4}}}(\cos ^2 x -\sin ^2 x)(\cos ^4 x + \sin ^ 4 x)dx\\
\\
&=&\int_0^{\scriptsize{\cfrac{\pi}{4}}}\cos 2x \big\{(\cos ^2 x + \sin ^ 2 x)^2-2\sin ^2x \cos ^2 x\big\}dx\\
\\
&=&\int_0^{\scriptsize{\cfrac{\pi}{4}}}\cos 2x (1-2\sin ^2x \cos ^2 x)dx\\
\\
&=&\int_0^{\scriptsize{\cfrac{\pi}{4}}}\cos 2x \big(1-\cfrac{1}{2}\sin ^2 2x \big)dx\\
\\
&=&\int_0^{\scriptsize{\cfrac{\pi}{4}}}\big(\cos 2x -\cfrac{1}{2}\cos 2x \sin ^2 2x \big)dx\\
\\
& & \hspace{10em}(\ \ (\sin ^3 2x)'=6\cos 2x \sin ^2 2x \ \ より)\\
\\
&=&\cfrac{1}{2} -\cfrac{1}{12} \big[\sin ^3 2x \big] _0^{\scriptsize{\cfrac{\pi}{4}}}\\
\\
&=&\cfrac{1}{2}- \cfrac{1}{12} \times \sin ^3 \cfrac{\pi}{2}\\
\\
&=&\cfrac{5}{12}\\
\end{eqnarray*}
ページの先頭へ↑
メインメニュー に戻る

