早稲田大学(理系) 2025年　問題Ⅳ


$空間内に原点 \ O\ を中心とする半径 \ r\ の球面 \ S\ がある。さらに、半径が \ 1,\ 2,\ 3\ の球面 \ S_1,\ S_2,\ S_3\ があり、$
$これら \ 4\ つの球面のうちどの \ 2\ つの球面も互いに外接している。S_1,\ S_2,\ S_3\ の中心を順に \ P_1,\ P_2,\ P_3\ とし、$
$O,\ P_1,\ P_2,\ P_3 \ は同一平面上にないとする。さらに、球面 \ S\ が球面 \ S_1,\ S_2,\ S_3\ と接する \ 3\ つの点と、$
$\vec{OQ}=\dfrac{1}{4}(\vec{OP_1}+ \vec{OP_2}+\vec{OP_3})\ \ により定まる点 \ Q\ は、同一平面上にあるとする。次の問に答えよ。$
$(1)\ \ rの値を求めよ。$
$(2)\ \ 四面体OP_1P_2P_3　の体積を求めよ。$


(1)

　

$この問題のイメージは \ 3\ 個のボール \ S_1,\ S_2,\ S_3\ をくっつけて、$

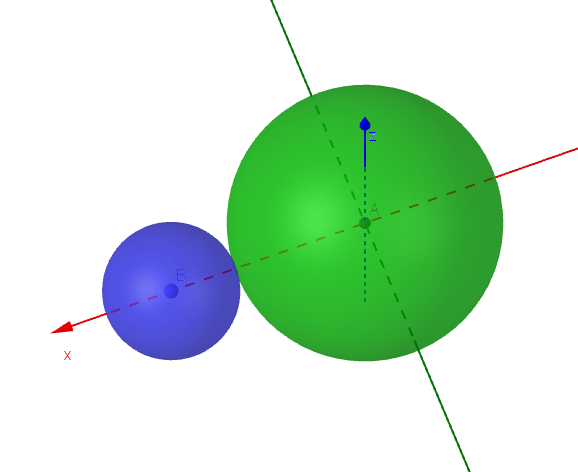
$その上にボール \ S\ をのせたものと考えればよい。$

$右図は球面 \ S\ と \ S_1\ が外接している様子を示したものである。$

$この図からわかるように、2つの球が外接するときは$

$接点は \ 2\ つの球面の中心を結ぶ線分上にあるから$

$中心間距離=(半径の和)\quad が成りたつ。$

(i)$\ \ 球面 \ S\ と球面 \ S_1,\ S_2,\ S_3\ が外接する条件は$

$\qquad OP_1=r+1,\quad OP_2=r+2,\quad OP_3=r+3$

(ii)$\ \ 球面 \ S_1,\ S_2,\ S_3\ が互いに外接する条件は$

$\qquad P_1P_2=3,\quad P_2P_3=5,\quad P_3P_1=4$

$球面 \ S\ と球面 \ S_1,\ S_2,\ S_3\ の接点をそれぞれ \ T_1,\ T_2,\ T_3\ とすると$

$OT_1=OT_2=OT_3=r \ \ だから$

　

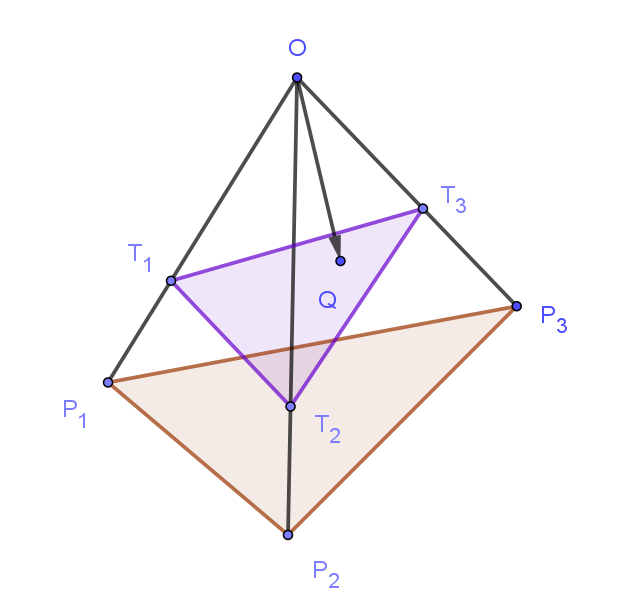
$\vec{OT_1}=\cfrac{r}{r+1}\vec{OP_1},\quad \vec{OT_2}=\cfrac{r}{r+2}\vec{OP_2},\quad \vec{OT_3}=\cfrac{r}{r+3}\vec{OP_3}$

$\vec{OQ}=\dfrac{1}{4}(\vec{OP_1}+ \vec{OP_2}+\vec{OP_3})\ \ により定まる点 \ Q\ は、$

$\triangle T_1T_2T_3 \ 上にあるから$

$\vec{T_1Q}=\alpha \vec{T_1T_2} + \beta \vec{T_1T_3}\ \ を満たす実数 \ \alpha,\ \ \beta \ が存在する。$

$\vec{OQ}-\vec{OT_1}=\alpha (\vec{OT_2}-\vec{OT_1}) + \beta (\vec{OT_3}- \vec{OT_1})$

$\vec{OQ}=(1-\alpha - \beta)\vec{OT_1}+\alpha \vec{OT_2} + \beta \vec{OT_3}$

$\dfrac{1}{4}(\vec{OP_1}+ \vec{OP_2}+\vec{OP_3}) =(1- \alpha - \beta ) \times \cfrac{r}{r+1}\vec{OP_1} + \alpha \times \cfrac{r}{r+2}\vec{OP_2} + \beta \times \cfrac{r}{r+3}\vec{OP_3} $

$4点 \ O,\ P_1,\ P_2,\ P_3 \ は同一平面上にないから$

\[ \hspace{1em} \left\{ \begin{array}{l} (1- \alpha - \beta ) \times \cfrac{r}{r+1}=\cfrac{1}{4} \hspace{5.5em}①\\ \alpha \times \cfrac{r}{r+2}=\cfrac{1}{4}　\hspace{9em}②\\ \beta \times \cfrac{r}{r+3}=\cfrac{1}{4} \hspace{10em}③\\ \end{array} \right. \]
$②,③より \quad \alpha=\cfrac{r+2}{4r},\quad \beta=\cfrac{r+3}{4r}$

$これらを①に代入して$

$(1- \cfrac{r+2}{4r} - \cfrac{r+3}{4r}) \times \cfrac{r}{r+1}=\cfrac{1}{4}$

$\cfrac{2r-5}{4r} \times \cfrac{r}{r+1}=\cfrac{1}{4}$

$2r-5=r+1$

$\therefore \ \ r=6$


(2)


$\vec{OP_1}=\vec{p_1},\ \ \vec{OP_2}=\vec{p_2},\ \ \vec{OP_3}=\vec{p_3}\ \ と表すことにする。$

$(1) より \ r=6\ だから \ \ OP_1=7,\ \ OP_2=8,\ \ OP_3=9 $

(i)$\ \ P_1P_2=3 \ \ より \ \ |\vec{P_1P_2}|=3$

$\quad |\vec{p_2}-\vec{p_1}|^2=9$

$\quad |\vec{p_2}|^2+|\vec{p_1}|^2-2\vec{p_1} \cdot \vec{p_2}=9$

$\quad 8^2+7^2-2\vec{p_1}\cdot \vec{p_2}=9$

$\quad \therefore \ \ \vec{p_1}\cdot \vec{p_2}=52$

(ii)$\ \ P_2P_3=5 \ \ より \ \ |\vec{P_2P_3}|=5$

$\quad |\vec{p_3}-\vec{p_2}|^2=25$

$\quad |\vec{p_3}|^2+|\vec{p_2}|^2-2\vec{p_2} \cdot \vec{p_3}=25$

$\quad 9^2+8^2-2\vec{p_2}\cdot \vec{p_3}=25$

$\quad \therefore \ \ \vec{p_2}\cdot \vec{p_3}=60$

(iii)$\ \ P_3P_1=4 \ \ より \ \ |\vec{P_3P_1}|=16$

$\quad |\vec{p_1}-\vec{p_3}|^2=16$

$\quad |\vec{p_1}|^2+|\vec{p_3}|^2-2\vec{p_1} \cdot \vec{p_3}=16$

$\quad 7^2+9^2-2\vec{p_1}\cdot \vec{p_3}=16$

$\quad \therefore \ \ \vec{p_1}\cdot \vec{p_3}=57$

$点 \ O\ から三角形P_1P_2P_3\ に垂線を下し、交点を \ H\ とする。$

　

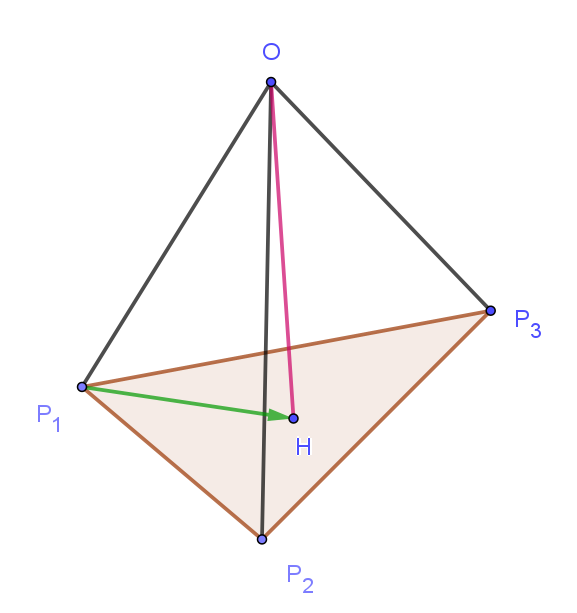
$\vec{P_1H}=s \vec{P_1P_2} + t \vec{P_1P_3} \ \ を満たす実数 \ s,\ t\ が存在する。$

$\vec{OH}-\vec{p_1}=s (\vec{p_2}-\vec{p_1}) + t (\vec{p_3}- \vec{p_1})$

$\vec{OH}=(1-s - t)\vec{p_1}+s \vec{p_2} + t \vec{p_3}$

(i)$\ \ \vec{OH} \perp \vec{P_1P_2} \ \ だから$

$\quad \vec{OH} \cdot (\vec{p_2}-\vec{p_1})=0$

$\quad \{(1-s - t)\vec{p_1}+s \vec{p_2} + t \vec{p_3}\} \cdot (\vec{p_2}-\vec{p_1})=0$

$\quad (1-s - t)(\vec{p_1}\cdot \vec{p_2} - |\vec{p_1}|^2) + s (|\vec{p_2}|^2-\vec{p_1} \cdot \vec{p_2} ) + t (\vec{p_2} \cdot \vec{p_3}-\vec{p_1}\cdot \vec{p_3})=0$

$\quad (1-s - t)(52 - 49) +s (64-52) + t (60 -57)=0$

$\quad 3s+1=0 \qquad \therefore s=-\cfrac{1}{3}$

(ii)$\ \ \vec{OH} \perp \vec{P_1P_3} \ \ だから$

$\quad \vec{OH} \cdot (\vec{p_3}-\vec{p_1})=0$

$\quad \{(1-s - t)\vec{p_1}+s \vec{p_2} + t \vec{p_3}\} \cdot (\vec{p_3}-\vec{p_1})=0$

$\quad (1-s - t)(\vec{p_1}\cdot \vec{p_3} - |\vec{p_1}|^2) + s (\vec{p_2} \cdot \vec{p_3} -\vec{p_1} \cdot \vec{p_2} ) + t (|\vec{p_3}|^2 -\vec{p_1}\cdot \vec{p_3})=0$

$\quad (1-s - t)(57 - 49) +s (60-52) + t (81 -57)=0$

$\quad 2t+1=0 \qquad \therefore t=-\cfrac{1}{2}$

$よって \quad \vec{OH}=(1+\dfrac{1}{3} + \dfrac{1}{2})\vec{p_1}-\dfrac{1}{3} \vec{p_2} - \dfrac{1}{2} \vec{p_3}=\dfrac{11}{6} \vec{p_1}-\dfrac{1}{3} \vec{p_2} - \dfrac{1}{2} \vec{p_3}$

\begin{eqnarray*} |\vec{OH}|^2 &=&\dfrac{121}{36}|\vec{p_1}|^2 +\dfrac{1}{9}|\vec{p_2}|^2+ \dfrac{1}{4}|\vec{p_3}|^2 -2 \times \dfrac{11}{6} \times \dfrac{1}{3} \times \vec{p_1} \cdot \vec{p_2} + 2 \times \dfrac{1}{3} \times \dfrac{1}{2} \times \vec{p_2}\cdot \vec{p_3} -2 \times \dfrac{1}{2} \times \dfrac{11}{6} \times \vec{p_1} \cdot \vec{p_3}\\ \\ &=&\dfrac{121}{36} \times 49 +\dfrac{1}{9} \times 64 + \dfrac{1}{4} \times 81 -2 \times \dfrac{11}{6} \times \dfrac{1}{3} \times 52 + 2 \times \dfrac{1}{3} \times \dfrac{1}{2} \times 60 -2 \times \dfrac{1}{2} \times \dfrac{11}{6} \times 57\\ \\ &=&44 \end{eqnarray*} $\therefore \ \ |\vec{OH}|=\sqrt{44}=2\sqrt{11}$

$(1)より \quad P_1P_2=3,\quad P_2P_3=5,\quad P_3P_1=4 \ \ だから \ \ \triangle P_1P_2P_3 \ は \ P_2P_3\ を斜辺とする直角三角形$

$したがって \quad \triangle P_1P_2P_3=\cfrac{1}{2} \times P_1P_2 \times P_1P_3=6$

$四面体OP_1P_2P_3 \ \ の体積 \ V\ は$

$V=\cfrac{1}{3} \times \triangle P_1P_2P_3 \times OH=\cfrac{1}{3} \times 6 \times 2\sqrt{11}=4\sqrt{11}$


ページの先頭へ↑



メインメニュー　に戻る