早稲田大学(理系) 2025年　問題Ⅱ


$xy\ 平面上で、連立不等式 \ \ 0 < x \leqq 1, \ \ 0 \leqq y \leqq \log \dfrac{1}{x}\ \ で定まる領域と \ y\ 軸の \ \ y \geqq 0 \ \ の部分を合わせた図形を$
$D\ とする。D\ に含まれる三角形の面積の最大値を求めよ。$


$D\ に含まれる三角形の面積が最大となるのは、三角形の \ 3\ つの頂点、あるいは \ 3\ 辺が \ D\ の境界にあるときである。$

$曲線 \ \ y=\log \dfrac{1}{x}=-\log x \ \ は下に凸だからこの曲線上にある \ 2\ 点を結ぶ線分は、この曲線の上側にある。$

$したがって、面積が最大になる三角形は、1\ 辺がこの曲線の接線の場合である。$

$このとき、右図から明らかなように、\triangle OAB \ \ が求める三角形である。$

　

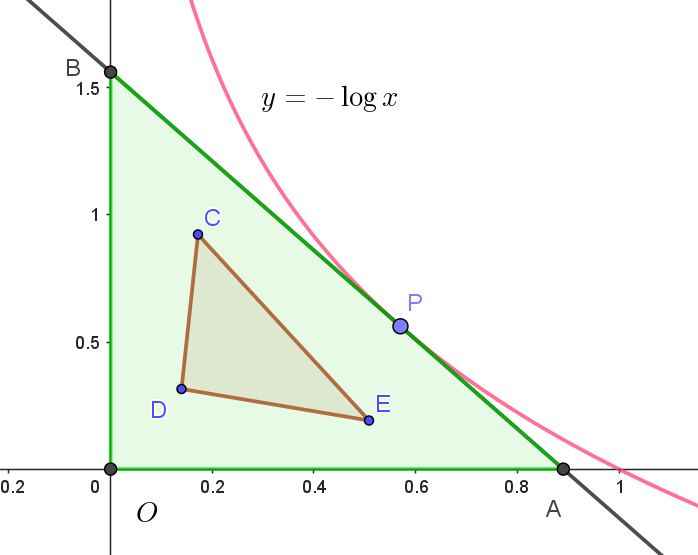
$y=\log \dfrac{1}{x}=-\log x \quad より \quad y'=-\cfrac{1}{x}$

$P(t,\ -\log t) \ \ (0 < t \leqq 1)\ \ における接線は$

$y=-\cfrac{1}{t}(x-t)-\log t $

$すなわち \quad y=-\cfrac{1}{t}x +1-\log t$

$x\ 軸との交点は \ \ A(t(1-\log t),\ 0)$

$y\ 軸との交点は \ \ B(0,\ 1-\log t)$

$\triangle OAB=\cfrac{1}{2} \times t(1-\log t) \times (1-\log t)=\cfrac{1}{2}t(1-\log t)^2$

$f(t)=\cfrac{1}{2}t(1-\log t)^2 \ \ (0 < t \leqq 1)\ \ とおくと$
\begin{eqnarray*} f'(t) &=&\cfrac{1}{2}(1-\log t)^2+\cfrac{1}{2}t \times 2(1-\log t)(-\dfrac{1}{t})\\ \\ &=&\cfrac{1}{2}(1-\log t)\big\{(1-\log t) -2\big\}\\ \\ &=&-\cfrac{1}{2}(1-\log t)(1+\log t) \\ \end{eqnarray*} $f'(t)=0 \ \ より \ \ 0 < t \leqq 1 \ \ だから \quad \log t=-1 \qquad t=\cfrac{1}{e}$
$増減表$
\[ \begin{array}{c||c|c|c|c|c} t& 0 & \cdots & \dfrac{1}{e} & \cdots & 1\\ \hline f'(t)& & + & 0 & - & \\ \hline f(t)& & \nearrow & 極大 & \searrow & \\ \end{array} \]
$f(t) \ は \ \ t=\cfrac{1}{e}\ \ のとき極大かつ最大となり、f(\dfrac{1}{e})=\cfrac{1}{2} \times \dfrac{1}{e}((1-\log \dfrac{1}{e})^2=\cfrac{2}{e}$

$よって、D\ に含まれる三角形の面積の最大は、 A(\dfrac{2}{e},\ 0),\ \ B(0,\ 2)\ とした \ \triangle OAB \ で最大値は \ \ \cfrac{2}{e}$


　

$(補充)$

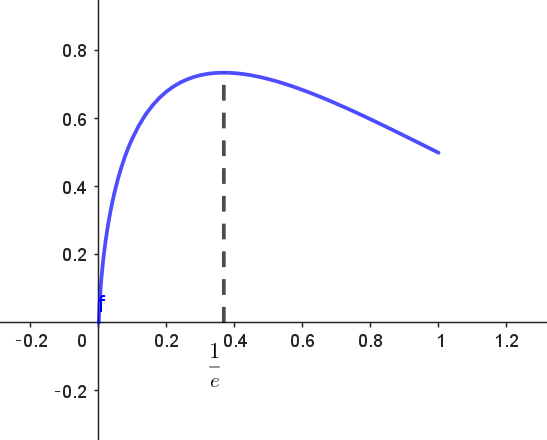
$f(t)=0\ \ より \ \ t=0,\quad f(1)=\cfrac{1}{2}$

$これらのことから \ y=f(t)\ のグラフは右図のとおり$


ページの先頭へ↑



メインメニュー　に戻る