早稲田大学(理系) 2025年　問題Ⅰ


$複素数平面上で、複素数 \ z\ が円 \ |z|=1\ の上を動くとき、w=\big(\dfrac{1+\sqrt{2}}{2}\big)z+\big(\dfrac{1-\sqrt{2}}{2}\big)\dfrac{1}{z} \ \ を満たす点 \ w\ の$
$の軌跡を \ C\ とする。次の問に答えよ。$
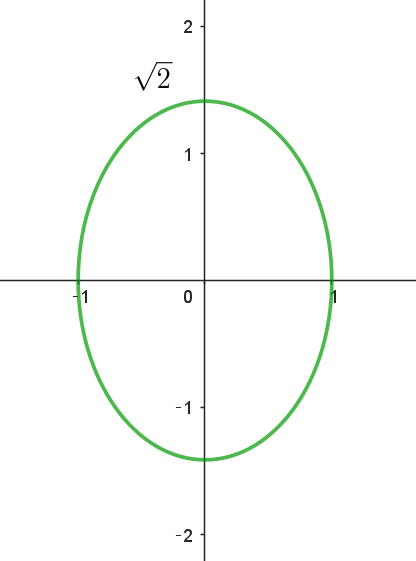
$(1)\ \ C\ はどのような図形か、複素数平面上に図示せよ。$
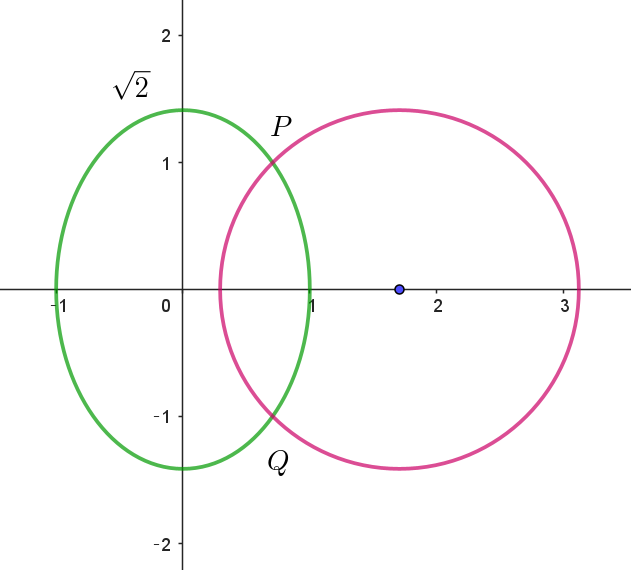
$(2)\ \ C\ と円 \ \big|z-\dfrac{2+\sqrt{2}}{2}\big|=\sqrt{2}\ \ の共有点を求めよ。$
$(3)\ \ C\ で囲まれる領域と \ \big|z-\dfrac{2+\sqrt{2}}{2}\big| \leqq \sqrt{2} \ \ の表す領域の共通部分の面積を求めよ。$


(1)


$z\ を極形式で表すと、|z|=1 \ \ だから \ \ z=\cos \theta + i\sin \theta \ \ とおける。$

$このとき \quad \cfrac{1}{z}=\cos \theta - i\sin \theta \quad だから$

　

\begin{eqnarray*} w &=&\big(\dfrac{1+\sqrt{2}}{2}\big)z+\big(\dfrac{1-\sqrt{2}}{2}\big)\dfrac{1}{z}\\ \\ &=&\big(\dfrac{1+\sqrt{2}}{2}\big)(\cos \theta + i\sin \theta) + \big(\dfrac{1-\sqrt{2}}{2}\big)(\cos \theta - i\sin \theta)\\ \\ &=&\big(\dfrac{1+\sqrt{2}}{2} + \dfrac{1-\sqrt{2}}{2}\big)\cos \theta + i \big(\dfrac{1+\sqrt{2}}{2} - \dfrac{1-\sqrt{2}}{2}\big)\sin \theta \\ \\ &=&\cos \theta + i \sqrt{2} \sin \theta \\ \end{eqnarray*} $w=x+yi\ \ (x,\ y \ は実数)\ \ とおくと$

$x=\cos \theta,\quad y=\sqrt{2}\sin \theta$

$\cos ^2 \theta + \sin ^2\theta=1 \quad に代入して$

$x^2+\big(\cfrac{y}{\sqrt{2}}\big)^2=1$

$C は右図のような楕円を表す$


(2)


$(1)より \quad C:2x^2+y^2=2 $

$y^2=2(1-x^2) \hspace{5em}①$

$円 \ \ \big|z-\dfrac{2+\sqrt{2}}{2}\big|=\sqrt{2}\ \ は \ \ z=x+yi \ \ (x,\ y \ は実数)\ \ とおくと$

$\big|(x-\dfrac{2+\sqrt{2}}{2})+yi\big|=\sqrt{2}$

　

$\big(x-\dfrac{2+\sqrt{2}}{2}\big)^2+y^2=2 \hspace{5em}②$

$①を②に代入して$

$\big(x-\dfrac{2+\sqrt{2}}{2}\big)^2+2(1-x^2)=2$

$x^2+(2+\sqrt{2})x - \big(\dfrac{2+\sqrt{2}}{2}\big)^2=0$

$2x^2+2(2+\sqrt{2})x - (3+2\sqrt{2})=0$

$2x^2+2\sqrt{2}(\sqrt{2}+1)x - (\sqrt{2}+1)^2=0$

$①より \quad -1 < x < 1 \quad だから$

$x=\cfrac{-\sqrt{2}(\sqrt{2}+1)+\sqrt{2(\sqrt{2}+1)^2+2(\sqrt{2}+1)^2}}{2}=\cfrac{-\sqrt{2}(\sqrt{2}+1)+2(\sqrt{2}+1)}{2}=\cfrac{\sqrt{2}}{2}$

$①に代入して \quad y^2=2(1-\dfrac{1}{2})=1$

$よって、C\ と円の共有点は \ \ P(\dfrac{\sqrt{2}}{2}+i), \quad Q(\dfrac{\sqrt{2}}{2}-i)$

　

(3)


(i)$\ \ S_1 を求める$

$①より 楕円 \ C\ は \quad y=\sqrt{2(1-x^2)}\quad だから$

\[S_1=\int_{\scriptsize{\dfrac{\sqrt{2}}{2}}}^1 \sqrt{2(1-x^2)}dx=\sqrt{2} \int_{\scriptsize{\dfrac{\sqrt{2}}{2}}}^1 \sqrt{1-x^2}dx\]
$(ア)\ \ この定積分を図形的に求める方法$

　

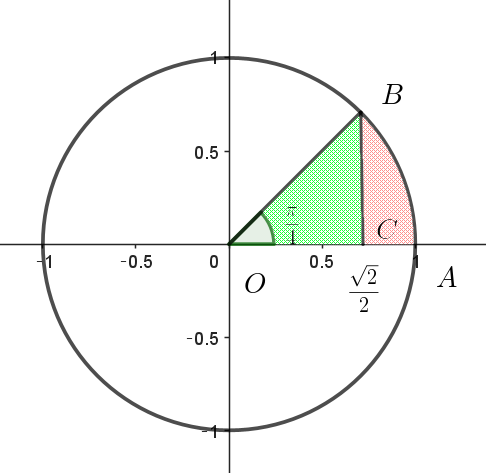
$\quad y=\sqrt{1-x^2}\ \ は原点中心、半径 \ 1\ の円で積分区間が \ \ [\dfrac{\sqrt{2}}{2},\ 1] \ \ だから$

\begin{eqnarray*} \quad S_1 &=&\sqrt{2} \times \big(中心角\dfrac{\pi}{4} の扇型OAB -\triangle OBC \big)\\ \\ &=&\sqrt{2}\big(\pi \times 1^1 \times \cfrac{1}{8} - \dfrac{1}{2} \times \cfrac{\sqrt{2}}{2} \times \dfrac{\sqrt{2}}{2}\big)\\ \\ &=&\sqrt{2}\big(\cfrac{\pi}{8}-\cfrac{1}{4}\big) \end{eqnarray*}
$(イ)\ \ この定積分を計算で求める方法$
\[ \quad x=\cos t \quad とおくと \quad dx=-\sin tdt \qquad \quad \begin{array}{c|c} x & \dfrac{\sqrt{2}}{2} \rightarrow 1 \\ \hline t & \ \dfrac{\pi}{4} \rightarrow 0 \\ \end{array} \] \begin{eqnarray*} S_1 &=&\sqrt{2} \int_{\scriptsize{\dfrac{\sqrt{2}}{2}}}^1 \sqrt{1-x^2}dx\\ \\ &=&\sqrt{2} \int_{\scriptsize{\dfrac{\pi}{4}}}^0 \sqrt{1-\cos^2 t}(-\sin t)dt\\ \\ &=&\sqrt{2} \int_0^{\scriptsize{\dfrac{\pi}{4}}} \sin ^2tdt\\ \\ &=&\cfrac{\sqrt{2}}{2} \int_0^{\scriptsize{\dfrac{\pi}{4}}}(1-\cos 2t)dt\\ \\ &=&\cfrac{\sqrt{2}}{2} \big[t-\dfrac{1}{2}\sin 2t\big] _0^{\scriptsize{\dfrac{\pi}{4}}}\\ \\ &=&\cfrac{\sqrt{2}}{2} \big(\dfrac{\pi}{4}-\dfrac{1}{2}\sin \dfrac{\pi}{2}\big) \\ \\ &=&\sqrt{2}\big(\cfrac{\pi}{8}-\cfrac{1}{4}\big) \end{eqnarray*} (ii)$\ \ S_2 を求める$

$\quad 円 \ \big(x-\dfrac{2+\sqrt{2}}{2}\big)^2+y^2=2 \ \ と \ x\ 軸との交点のうち$

$\quad 中心より原点側にある点 \ F\ は$

$\quad x-\dfrac{2+\sqrt{2}}{2} =-\sqrt{2} \ \ より \quad x=\dfrac{2+\sqrt{2}}{2}-\sqrt{2}=\cfrac{2-\sqrt{2}}{2}$

$\quad 積分区間が \ \ [\dfrac{2-\sqrt{2}}{2},\ \dfrac{\sqrt{2}}{2}]\ だから$

\[\quad S_2=\int_{\scriptsize{\dfrac{2-\sqrt{2}}{2}}}^{\scriptsize{\dfrac{\sqrt{2}}{2}}} \sqrt{2-(x-\dfrac{2+\sqrt{2}}{2})^2}dx\]
$(ア)\ \ この定積分を図形的に求める方法$

　

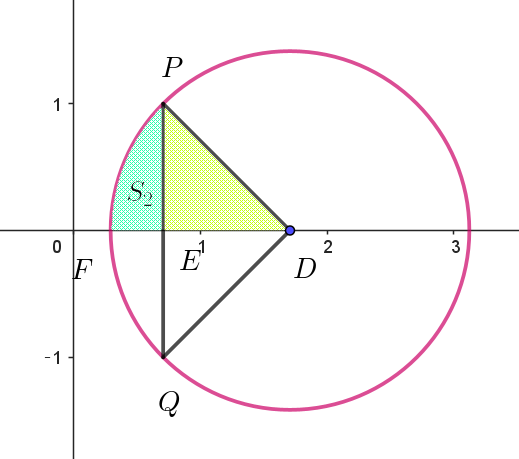
$\quad この円は、中心 \ D(\dfrac{2+\sqrt{2}}{2},\ 0)、\ \ 半径 \ \ \sqrt{2} \ \ だから$

$\quad DE=\dfrac{2+\sqrt{2}}{2}-\dfrac{\sqrt{2}}{2}=1,\quad PE=1$

$\quad したがって \quad \angle PDE=\cfrac{\pi}{4}$
\begin{eqnarray*} \quad S_2 &=&\big(中心角 \ \dfrac{\pi}{4}\ の扇型 \ DPF - \triangle DPE \big)\\ \\ &=&\pi \times (\sqrt{2})^2 \times \cfrac{1}{8} - \dfrac{1}{2} \times 1 \times 1\\ \\ &=&\cfrac{\pi}{4}-\cfrac{1}{2} \end{eqnarray*}
$(イ)\ \ この定積分を計算で求める方法$
\[ \quad x-\cfrac{2+\sqrt{2}}{2}=\sqrt{2}\cos t \quad とおくと \quad dx=-\sqrt{2}\sin tdt \qquad \begin{array}{c|c} x & \dfrac{2-\sqrt{2}}{2} \rightarrow \dfrac{\sqrt{2}}{2}\\ \hline t & \pi \rightarrow \dfrac{3}{4}\pi\\ \end{array} \]
\begin{eqnarray*} S_2 &=&\int_{\scriptsize{\dfrac{2-\sqrt{2}}{2}}}^{\scriptsize{\dfrac{\sqrt{2}}{2}}} \sqrt{2-(x-\dfrac{2+\sqrt{2}}{2})^2}dx\\ \\ &=&\int_{\pi}^{\scriptsize{\dfrac{3}{4}\pi}} \sqrt{2-2\cos ^2t}(-\sqrt{2}\sin t)dt\\ \\ &=&2\int_{\scriptsize{\dfrac{3}{4}\pi}}^{\pi} \sin ^2tdt\\ \\ &=&\int_{\scriptsize{\dfrac{3}{4}\pi}}^{\pi} (1-\cos 2t)dt\\ \\ &=&\big[t-\dfrac{1}{2}\sin 2t\big] _{\scriptsize{\dfrac{3}{4}\pi}}^{\pi}\\ \\ &=&\big(\pi-\dfrac{1}{2}\sin 2\pi \big)-\big(\dfrac{3}{4}\pi -\dfrac{1}{2}\sin \dfrac{3\pi}{2}\big)\\ \\ &=&\cfrac{\pi}{4}-\cfrac{1}{2} \end{eqnarray*}

$以上より求める面積 \ S\ は$

\begin{eqnarray*} S &=&2(S_1+S_2)\\ \\ &=&2\big(\sqrt{2}(\cfrac{\pi}{8}-\cfrac{1}{4})+(\cfrac{\pi}{4}-\cfrac{1}{2}\big)\\ \\ &=&\cfrac{2+\sqrt{2}}{4}\pi -\cfrac{2+\sqrt{2}}{2} \end{eqnarray*}

ページの先頭へ↑



メインメニュー　に戻る