MY MATH NOTE

$極座標で \ \ r=r(\theta)\ \ (\alpha \leqq \theta \leqq \beta )\ \ と表わされる曲線の始線の回りに回転してできる回転体の体積は$
\[\hspace{4em} V=\cfrac{2\pi}{3} \int _{\alpha}^{\beta} r^3\sin \theta d\theta\]

　
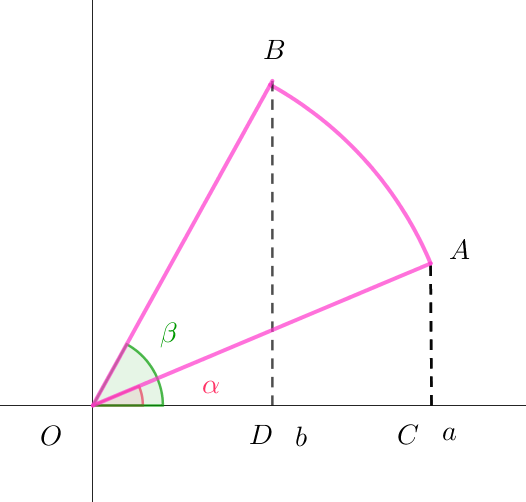
$(証明)$

$x=r\cos \theta \ \ より \ \ dx=(\cfrac{dr}{d\theta}\cos \theta - r\sin \theta )d\theta \quad だから$

\begin{eqnarray*} & &(弧 \ AB\ の部分の回転体の体積)\\ \\ &=&\pi \int _b^a y^2dx\\ \\ &=&\pi \int _{\beta}^{\alpha}(r\sin \theta)^2(\cfrac{dr}{d\theta}\cos \theta -r\sin \theta )d\theta \\ \\ &=&\pi \int _{\beta}^{\alpha}r^2 \cfrac{dr}{d\theta} \sin ^2 \theta \cos \theta d\theta - \pi \int _{\beta}^{\alpha} r^3\sin ^3\theta d\theta \\ \\ &=&\pi \big[\cfrac{r^3}{3} \sin ^2 \theta \cos \theta \big] _{\beta}^{\alpha} -\pi \int _{\beta}^{\alpha} \cfrac{r^3}{3}(2\sin \theta \cos ^2 \theta -\sin ^3 \theta)d\theta - \pi \int _{\beta}^{\alpha} r^3\sin ^3\theta d\theta \\ \\ &=&\cfrac{\pi}{3}r(\alpha)^3 \sin ^2 \alpha \cos \alpha - \cfrac{\pi}{3} r(\beta)^3\sin ^2 \beta \cos \beta -\cfrac{2\pi}{3} \int _{\beta}^{\alpha} r^3\sin \theta (\cos ^2 \theta +\sin ^2 \theta)d\theta \\ \\ &=&\cfrac{\pi}{3}(r(\alpha) \sin \alpha )^2 (r(\alpha)\cos \alpha ) - \cfrac{\pi}{3} (r(\beta)\sin \beta)^2(r(\beta) \cos \beta) -\cfrac{2\pi}{3} \int _{\beta}^{\alpha} r^3\sin \theta d\theta \\ \\ &=&\cfrac{\pi}{3}AC^2 \cdot OC - \cfrac{\pi}{3} BD^2 \cdot OD +\cfrac{2\pi}{3} \int _{\alpha}^{\beta} r^3\sin \theta d\theta \\ \\ &=&(線分OAの回転体の体積)-(線分OBの回転体の体積)+ \cfrac{2\pi}{3} \int _{\alpha}^{\beta} r^3\sin \theta d\theta \\ \end{eqnarray*} $求める体積 \ V\ は$
\begin{eqnarray*} V &=&(弧 \ AB\ の部分の回転体の体積)+(線分 \ OB\ の回転体の体積)-(線分 \ OA\ の回転体の体積) \\ \\ &=&\cfrac{2\pi}{3} \int _{\alpha}^{\beta} r^3\sin \theta d\theta \end{eqnarray*}

　
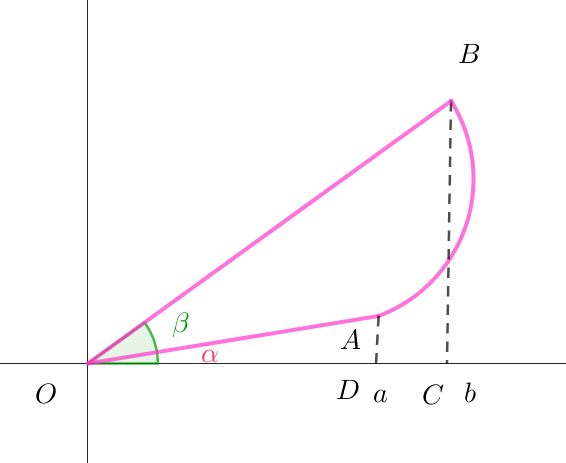
$なお、右図のように \ \ a < b \ \ の場合は上と同様にして$
\begin{eqnarray*} & &(弧 \ AB\ の部分の回転体の体積) \\ &=&(線分 \ OB\ の回転体の体積)-(線分 \ OA\ の回転体の体積)-\cfrac{2\pi}{3} \int _{\alpha}^{\beta} r^3\sin \theta d\theta\\ \end{eqnarray*} $が導かれ、$
\begin{eqnarray*} V &=&(線分 \ OB\ の回転体の体積)-(線分 \ OA\ の回転体の体積)-(弧 \ AB\ の部分の回転体の体積) \\ \\ &=&\cfrac{2\pi}{3} \int _{\alpha}^{\beta} r^3\sin \theta d\theta \end{eqnarray*}

ページの先頭へ↑