$x=a\cos ^4 \theta ,\quad y=a\sin ^4 \theta \ \ (a > 0)\ \ で表される曲線の回転体の体積$
$曲線 \ \ x=a\cos ^4 t ,\quad y=a\sin ^4 t \ \ (a > 0)\ \ で表される曲線は放物線でした。$
$\quad 詳しくは \ \ $$x=a\cos ^4 \theta ,\quad y=a\sin ^4 \theta \ \ で表される曲線$$\ \ をご覧ください。$
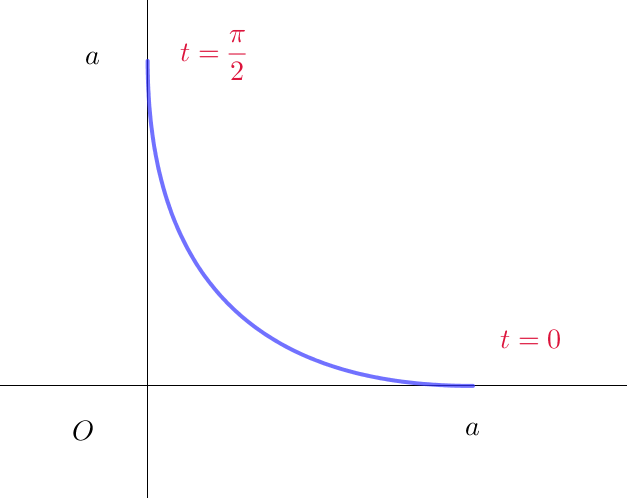
$この曲線を \ x\ 軸の回りに回転してできる回転体の体積 \ V\ を求めてみましょう。$
\begin{eqnarray*}
V
&=&\pi \int _0^a y^2 dx\\
\\
&=&\pi \int _{\scriptsize{\cfrac{\pi}{2}}}^0 (a\sin ^4 t)^2 \cdot 4a\cos ^3 t (-\sin t)dt\\
\\
&=&4\pi a^3 \int _0^{\scriptsize{\cfrac{\pi}{2}}} \sin ^9 t \cos ^3 t dt\\
\\
&=&4\pi a^3 \int _0^{\scriptsize{\cfrac{\pi}{2}}} \sin ^9 t (1- \sin ^2 t) \cos t dt\\
\end{eqnarray*}
\[\qquad \sin t=u \quad とおくと \quad
\cos t dt=du \qquad
\begin{array}{c|c}
t & 0 \ \ \rightarrow \scriptsize{\cfrac{\pi}{2}} \\
\hline
u & 0 \ \ \rightarrow 1 \\
\end{array}
\]
\begin{eqnarray*}
V
&=&4\pi a^3 \int _0^1 u^9(1-u^2) du\\
\\
&=&4\pi a^3 \int _0^1 (u^9-u^{11}) du\\
\\
&=&4\pi a^3 \big[\cfrac{u^{10}}{10}-\cfrac{u^{12}}{12}\big]_0^1\\
\\
&=&4\pi a^3 \big(\cfrac{1}{10}-\cfrac{1}{12}\big)\\
\\
&=&\cfrac{1}{15}\pi a^3
\end{eqnarray*}
媒介変数表示による曲線の回転体の体積メニュー に戻る
メインメニュー に戻る