カージオイドの回転体の体積
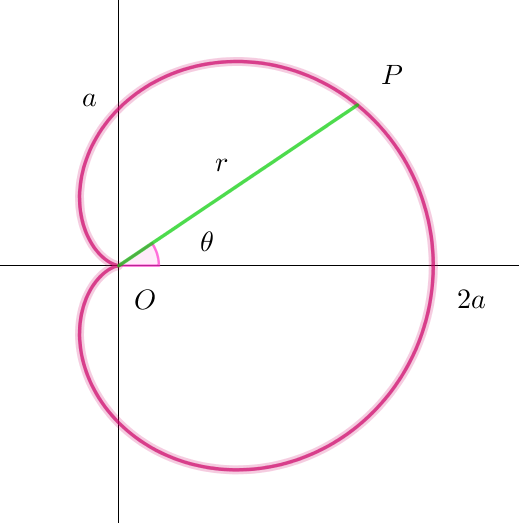
$極座標で \ \ r=a(1+\cos \theta)\ \ と表される図形をカージオイドといいます。$
$\qquad 詳しくは($カージオイド$)をご覧ください。$
$この図形を始線の回りに回転してできる回転体の体積を求めてみましょう。$
\begin{eqnarray*}
V
&=&\cfrac{2\pi}{3} \int _0^{\pi} r^3\sin \theta d\theta\\
\\
&=&\cfrac{2\pi}{3} \int _0^{\pi} a^3(1+\cos \theta )^3 \sin \theta d\theta\\
\\
\end{eqnarray*}
\[
t=\cos \theta \quad とおくと \quad dt=-\sin \theta d\theta
\qquad
\begin{array}{c|c}
\theta & 0\ \ \rightarrow \pi \quad \\
\hline
t & \ 1 \rightarrow -1 \\
\end{array}
\quad だから
\]
\begin{eqnarray*}
V
&=&\cfrac{2\pi}{3}a^3 \int _1^{-1} (1+t )^3 (-dt)\\
\\
&=&\cfrac{2\pi}{3}a^3 \big[\cfrac{(1+t )^4}{4}\big]_{-1}^1\\
\\
&=&\cfrac{2\pi}{3}a^3 \times \cfrac{2^4}{4}\\
\\
&=&\cfrac{8}{3}\pi a^3
\end{eqnarray*}
極座標表示による回転体の体積メニュー に戻る
メインメニュー に戻る