アルキメデスの渦巻線
$といいます。$
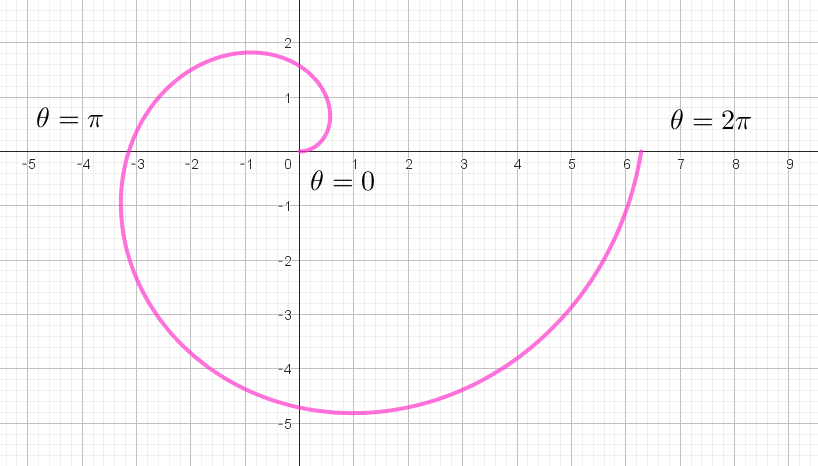
$右図は \ a=1\ の場合の \ \ 0 \leqq \theta \leqq 2\pi \ \ の部分のグラフです。$
$この図形の \ \ 0 \leqq \theta \leqq \pi \ \ の部分を始線の回りに回転してできる回転体の$
$体積を求めてみましょう。$
\[V=\cfrac{2\pi}{3} \int _0^{\pi} r^3\sin \theta d\theta=\cfrac{2\pi}{3}a^3 \int _0^{\pi} \theta ^3 \sin \theta d\theta\] $定積分の漸化式を求めます$
\begin{eqnarray*} I_n &=&\int _0^{\pi}\theta ^n \sin \theta d \theta\\ \\ &=&\big[-\theta ^n \cos \theta \big ]_0^{\pi} +\int _0^{\pi} n \theta ^{n-1} \cos \theta d \theta\\ \\ &=&\pi ^n + n \int _0^{\pi} \theta ^{n-1} \cos \theta d \theta\\ \\ &=&\pi ^n + n \Big\{ \big[\theta ^{n-1} \sin \theta \big ]_0^{\pi} -\int _0^{\pi} (n-1) \theta ^{n-2} \sin \theta d \theta \Big\}\\ \\ &=&\pi ^n - n(n-1) \int _0^{\pi} \theta ^{n-2} \sin \theta d \theta\\ \\ &=&\pi ^n - n(n-1) I_{n-2}\\ \end{eqnarray*} $ここで$
\[I_1=\int _0^{\pi}\theta \sin \theta d \theta=[-\theta \cos \theta ]_0^{\pi}+\int _0^{\pi} \cos \theta d \theta=\pi +\big [\sin \theta \big ]_0^{\pi}=\pi \quad だから\]
$I_3=\pi^3-3 \times 2 I_1=\pi ^3-6\pi$
$よって$
\[V=\cfrac{2\pi}{3} \int _0^{\pi} r^3\sin \theta d\theta=\cfrac{2\pi}{3}a^3 I_3=\cfrac{2\pi}{3}a^3 (\pi ^3-6\pi)=\cfrac{2}{3}\pi ^2(\pi ^2-6)a^3\]
極座標表示による回転体の体積メニュー に戻る
メインメニュー に戻る