宇都宮大学(理系) 2024年　問題4


$関数\ y=xe^{-2x} \ が極大値をとる \ x\ の値を \ a\ とする。また、m\ を \ 0\ でない定数として\ \ g(x)=\dfrac{1}{m}x \ \ とする。$
$曲線 \ y=f(x)\ と直線 \ y=g(x)\ は、原点以外に、x > a \ において共有点をもつとするとき、次の問いに答えよ。$
\[必要ならば、\lim_{x \rightarrow \infty} f(x)=0 \ \ を用いてよい。\] $(1)\ \ f(x)\ の増減を調べ、a\ の値を求めよ。$
$(2)\ \ m\ の値の範囲を求め、y=f(x)\ と \ y=g(x)\ の \ x> a \ における共有点の座標を \ m\ を用いて表せ。$
\[(3)\ \ 不定積分 \ \ \int f(x)dx \ \ を求めよ。\] $(4)\ \ 0 \leqq x \leqq a \ \ において、3\ つの直線 \ y=g(x),\ \ y=0,\ \ x=a \ \ で囲まれた部分の面積を \ S_1(m)\ とする。$
$\quad また、x \geqq a \ \ において、曲線 \ y=f(x) \ と \ 2\ つの直線 \ y=g(x),\ \ x=a \ \ で囲まれた部分の面積を \ S_2(m) \ とする。$
$\quad S(m)=S_1(m)+S_2(m) \ \ とするとき、S(m)\ を \ m\ を用いて表せ。$
$(5)\ \ (4)で求めた \ S(m)\ を最小にする \ m\ の値と、そのときの \ S(m)\ の値を求めよ。$


$(注意)$

$問題文に、「m\ を \ 0\ でない定数」とあるが、小問(5)では「 S(m)\ を最小にする \ m\ の値」を微分法で求めさせています。$

$よくあることだといえば、そうなのですが、m\ を定数でなく、「実数」としておけば問題なかったと思います。$

$もっとも、受験会場にいる受験生は気がつかなかったと思いますが$


(1)


$f(x)=xe^{-2x} \ \ より \ \ f'(x)=e^{-2x}-2xe^{-2x}=(1-2x)e^{-2x}$

$f'(x)=0 \ \ より \ \ x=\cfrac{1}{2}$

$増減表$
\[ \begin{array}{c||c|c|c|c|c} x& \cdots & \dfrac{1}{2} & \cdots \\ \hline f'(x)& + & 0 & - \\ \hline f(x)& \nearrow & 極大 & \searrow \\ \end{array} \]
$x=\cfrac{1}{2}\ で \ f(x)\ は極大となるから \ \ a=\cfrac{1}{2}$


(2)

　

$(1)において $

$極大値は \ \ f(\dfrac{1}{2})=\cfrac{1}{2}e^{-1}=\cfrac{1}{2e}$

$f(0)=0$

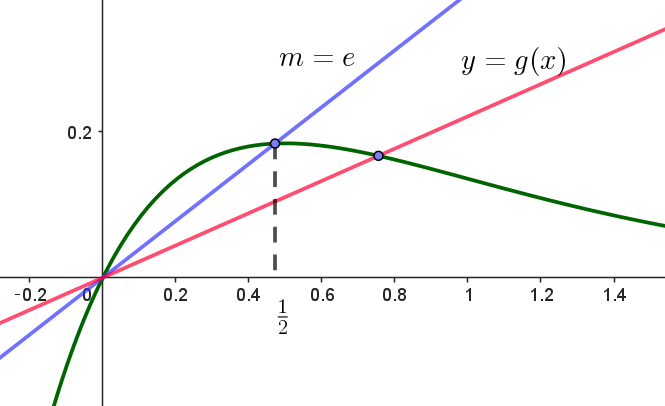
\[x \longrightarrow -\infty \ \ のとき \ \ f(x) \longrightarrow -\infty \] \[x \longrightarrow \infty \ \ のとき \ \ f(x) \longrightarrow 0\] $y=f(x)\ のグラフは右図のとおり$

$y=g(x)\ が極大点(\dfrac{1}{2},\ \cfrac{1}{2e})\ を通るとき \ \ m=\dfrac{1}{2} \times 2e=e$

$よって、曲線 \ y=f(x)\ と直線 \ y=g(x)\ が、原点以外に、x > a \ において共有点をもつのは$

$m > e \ \ のとき$

$このとき、y=f(x)\ と \ y=g(x)\ の 共有点の座標は$

$xe^{-2x}=\cfrac{x}{m}$

$e^{-2x}=\cfrac{1}{m} $

$-2x=\log \cfrac{1}{m}=-\log m$

$x=\cfrac{\log m}{2}$

$y=\cfrac{1}{m} \times \cfrac{\log m}{2}=\cfrac{\log m}{2m}$

$共有点の座標は \ \ (\cfrac{\log m}{2},\ \cfrac{\log m}{2m})$


(3)


\begin{eqnarray*} & &\int f(x)dx\\ \\ &=&\int xe^{-2x}dx\\ \\ &=&-\cfrac{1}{2}xe^{-2x} + \cfrac{1}{2}\int e^{-2x}dx\\ \\ &=&-\cfrac{1}{2}xe^{-2x} - \cfrac{1}{4}e^{-2x} +C \quad (Cは積分定数) \end{eqnarray*}

(4)

　

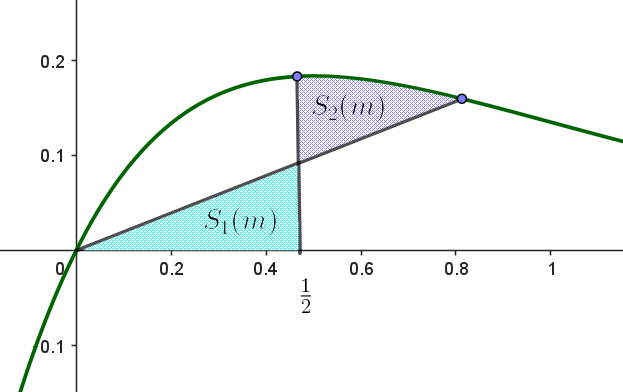
$S_1(m)=\cfrac{1}{2} \times \cfrac{1}{2} \times \cfrac{1}{2m}=\cfrac{1}{8m}$
\begin{eqnarray*} S_2(m) &=&\int _{\tfrac{1}{2}}^{\tfrac{\log m}{2}}(xe^{-2x}-\dfrac{x}{m})dx\\ \\ &=&\big[-\cfrac{1}{2}xe^{-2x} - \cfrac{1}{4}e^{-2x} -\dfrac{x^2}{2m}\big]_{\tfrac{1}{2}}^{\tfrac{\log m}{2}}\\ \\ &=&-\cfrac{1}{2} \times \cfrac{\log m}{2} \times \cfrac{1}{m} -\cfrac{1}{4} \times \cfrac{1}{m} -\cfrac{1}{2m}\big(\dfrac{\log m}{2}\big)^2+\\ \\ & & \qquad \cfrac{e^{-1}}{4}+\cfrac{e^{-1}}{4}+\cfrac{1}{8m}\\ \\ &=&-\cfrac{\log m}{4m} -\cfrac{1}{4m} -\cfrac{(\log m)^2}{8m}+\cfrac{1}{2e}+\cfrac{1}{8m}\\ \\ &=&-\cfrac{(\log m)^2}{8m} -\cfrac{\log m}{4m} -\cfrac{1}{8m} +\cfrac{1}{2e} \\ \end{eqnarray*} \begin{eqnarray*} S &=&S_1+S_2\\ \\ &=&\cfrac{1}{8m} -\cfrac{(\log m)^2}{8m} -\cfrac{\log m}{4m} -\cfrac{1}{8m} +\cfrac{1}{2e}\\ \\ &=&-\cfrac{(\log m)^2}{8m} -\cfrac{\log m}{4m} +\cfrac{1}{2e} \\ &=&-\cfrac{(\log m)^2+2\log m }{8m} +\cfrac{1}{2e} \end{eqnarray*}

(5)


$S(m)=-\cfrac{(\log m)^2+2\log m}{8m} +\cfrac{1}{2e} \ \ より$

$S'(m)=-\cfrac{1}{8}\big\{ \cfrac{\big(2\log m \times \dfrac{1}{m} +\dfrac{2}{m} \big)m -\big((\log m)^2+2\log m\big)}{m^2} \big\}= \cfrac{(\log m)^2 -2}{8m^2}$

$S'(m)=0 \ \ より \ \ m > 0 \ \ だから \ \ \log m=\sqrt{2} \qquad m=e^{\sqrt{2}}$

$増減表$
\[ \begin{array}{c||c|c|c|c|c} m & e & \cdots & e^{\sqrt{2}} & \cdots \\ \hline S'(m) & & - & 0 & + \\ \hline S(m)& & \searrow & 極小 & \nearrow \\ \end{array} \]
$m=e^{\sqrt{2}}\ \ で \ S(m)\ は極小かつ最小となり、最小値は$

$S(e^{\sqrt{2}})=-\cfrac{2+2\sqrt{2}}{8e^{\sqrt{2}}} + \cfrac{1}{2e}=\cfrac{1}{2e}-\cfrac{1+\sqrt{2}}{4e^{\sqrt{2}}}$


ページの先頭へ↑



メインメニュー　に戻る