宇都宮大学(理系) 2024年 問題3
$関数\ y=\dfrac{x+2}{2x+2}\ の逆関数を \ y=f(x)\ で表す。また、k\ を定数として \ g(x)=|2x+k|-3 \ と定める。$
$次の問いに答えよ。$
$(1)\ \ y=\dfrac{x+2}{2x+2}\ の定義域と値域を求めよ。$
$(2)\ \ f(x)\ を求め、y=f(x)\ のグラフをかけ。$
$(3)\ \ k=1 \ のとき、f(x) \geqq g(x) \ を満たす \ x\ の値の範囲を求めよ。$
$(4)\ \ y=f(x)\ のグラフと \ y=g(x)\ のグラフが接するときの \ k\ の値を求めよ。$
$(5)\ \ x \leqq 0 \ を満たすすべての \ x\ に対して \ f(x) < g(x)\ が成り立つような \ k\ の値の範囲を求めよ。$
(1)
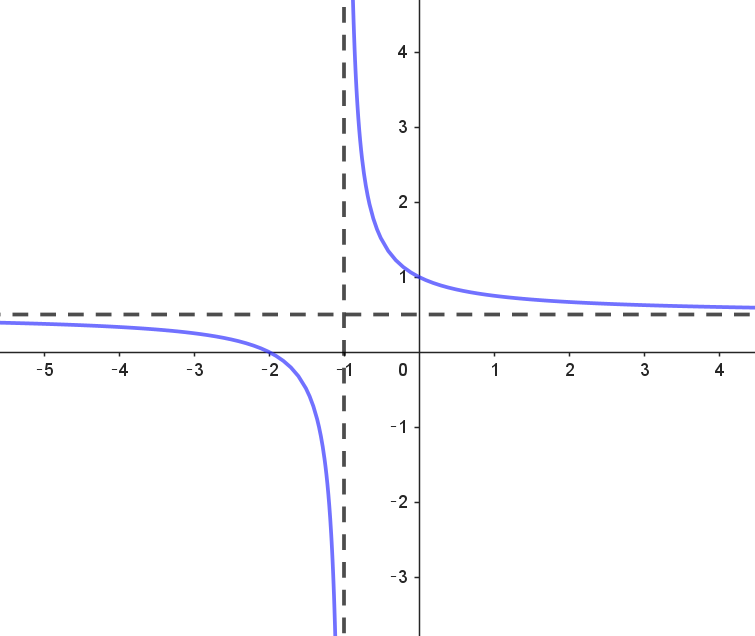
$定義域は \quad x=-1 \ \ を除くすべての実数$
$値域は \quad y=\cfrac{1}{2} \ \ をのぞくすべての実数$
(2)
$y=\cfrac{x+2}{2x+2} \quad の分母を払って$
$y(2x+2)=x+2$
$y \ne \cfrac{1}{2} \ \ だから \quad x=\cfrac{-2y+2}{2y-1}$
$x\ と \ y\ を交換して \quad y=\cfrac{-2x+2}{2x-1}$
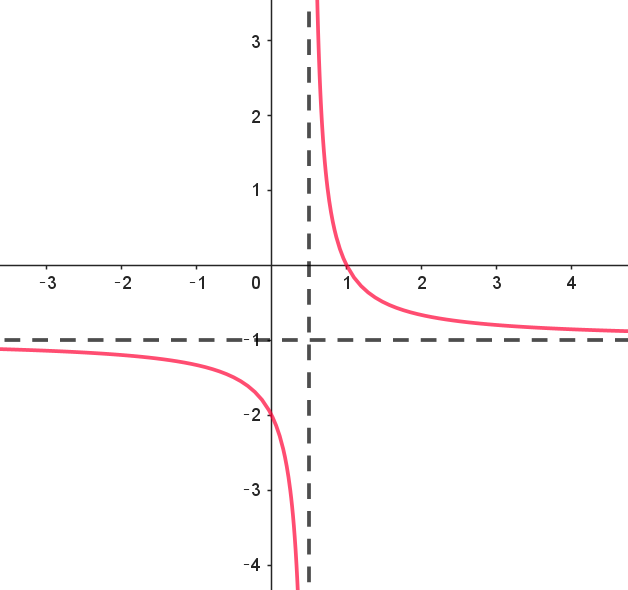
$よって \quad f(x)=\cfrac{-2x+2}{2x-1}=-1+\cfrac{1}{2x-1}$
$グラフは右図のとおり$
(3)
$k=1 \ \ のとき \quad g(x)=|2x+1|-3$
$f(x)\ と \ g(x)\ の交点の \ x\ 座標は$
(i)$\ \ x \leqq -\cfrac{1}{2} \quad のとき$
$\quad -1+\cfrac{1}{2x-1}=-(2x+1)-3$
$\quad \cfrac{1}{2x-1}=-(2x+3)$
$\quad 1=-(2x+3)(2x-1)$
$\quad 4x^2+4x-2=0$
$\quad 2x^2+2x-1=0$
$\quad x=\cfrac{-1 \pm \sqrt{3}}{2}$
$\quad x \leqq -\cfrac{1}{2} \quad だから \quad x=\cfrac{-1 -\sqrt{3}}{2}$
$\quad -1+\cfrac{1}{2x-1}=(2x+1)-3$
$\quad \cfrac{1}{2x-1}=2x-1$
$\quad 1=(2x-1)^2$
$\quad 2x-1=\pm 1$
$\quad x=1,\ \ 0 \quad これらはともに \ \ x \geqq -\cfrac{1}{2}\ \ をみたす。$
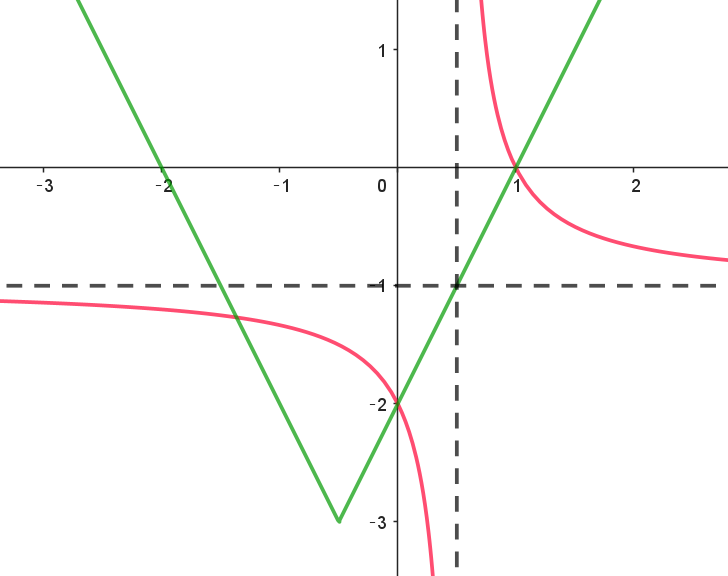
$y=f(x)\ と \ y=g(x)\ のグラフは右図のとおりで、f(x) \geqq g(x)\ \ を満たす \ x\ の値の範囲は$
$\cfrac{1-\sqrt{3}}{2} \leqq x \leqq 0 , \quad \cfrac{1}{2} < x \leqq 1 $
(4)
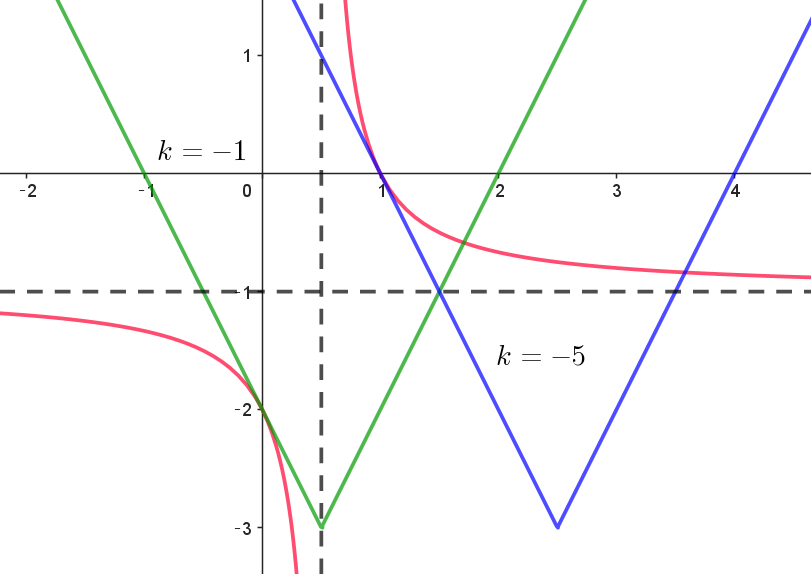
$右図のとおり \ \ x \leqq -\cfrac{k}{2}\ \ のときで、$
$g(x)=-(2x+k)-3=-2x-k-3 \ \ の場合である。$
$-1+\cfrac{1}{2x-1}=-2x-k-3$
$\cfrac{1}{2x-1}=-2x-k-2$
$-(2x+k+2)(2x-1)=1$
$4x^2+2(k+1)x-k-1=0$
$接する条件は$
$\cfrac{D}{4}=(k+1)^2+4(k+1)=0$
$(k+1)(k+1+4)=0$
$k=-1,\ \ -5$
$接点のx座標は \quad x=-\cfrac{k+1}{4} \quad だから \quad k=-1 \ \ のとき \ \ x=0, \qquad k=-5 \ \ のとき \ \ x=1$
$ともに \ \ x \leqq -\cfrac{k}{2}\ \ を満たしている。$
(5)
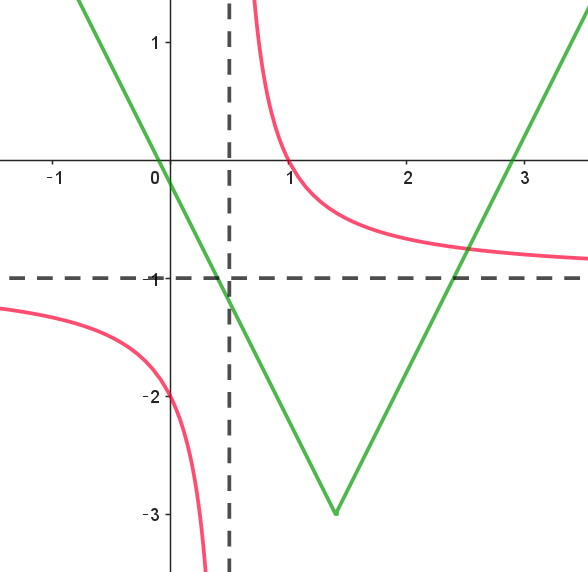
$右図からわかるとおり \quad k <-1$
メインメニュー に戻る