宇都宮大学(理系) 2024年　問題2


$座標平面上の点 \ P_1,\ P_2,\ P_3,\ P_4,\ \cdots \ が \ \ \vec{P_nP_{n+1}}=(1,\ 2^n) \ \ (n=1,\ 2,\ 3,\ \cdots ) \quad すなわち \quad \vec{P_1P_2}=(1,\ 2),$
$\vec{P_2P_3}=(1,\ 4),\quad \vec{P_3P_4}=(1,8),\ \ \cdots \ \ を満たしている。次の問いに答えよ。$
$(1)\ \ \vec{P_1P_3}\ \ および \ \ \vec{P_1P_4} \ \ を成分表示せよ。また、n=2,\ 3,\ 4,\ \cdots \ \ とするとき、\vec{P_1P_n} \ \ を \ n\ の式で成分表示せよ。$
$(2)\ \ \vec{a}=(a_1,\ a_2),\ \ \vec{b}=(b_1,\ b_2)\ とするとき、|\vec{a}|^2 |\vec{b}|^2 -(\vec{a} \cdot \vec{b})^2=(a_1b_2-a_2b_1)^2 \ \ が成り立つことを示せ。$
$(3)\ \ n=2,\ 3,\ 4,\ \cdots \ とするとき、P_1,\ P_n,\ P_{n+1}\ を頂点とする三角形の面積 \ S_n \ を \ n\ の式で表せ。$
$(4)\ \ n=3,\ 4,\ 5,\ \cdots \ \ とするとき、P_1,\ P_2,\ P_3,\ \cdots ,\ P_n \ を頂点とする \ n\ 角形の面積 \ T_n \ を \ n\ の式で表せ。$


(1)


$\vec{P_1P_3}=\vec{P_1P_2}+\vec{P_2P_3}=(1,\ 2)+(1,\ 4)=(2,\ 6)$

$\vec{P_1P_4}=\vec{P_1P_3}+\vec{P_3P_4}=(2,\ 6)+(1,\ 8)=(3,\ 14)$

\begin{eqnarray*} \vec{P_1P_n} &=&\vec{P_1P_2}+\vec{P_2P_3}+ \cdots + \vec{P_{n-1}P_n}\\ \\ &=&(1,\ 2)+(1,\ 4)+ \cdots + (1,\ 2^{n-1})\\ \\ &=&(n-1,\ 2+2^2+\cdots + 2^{n-1})\\ \\ &=&(n-1,\ \dfrac{2(2^{n-1}-1)}{2-1})\\ \\ &=&(n-1,\ 2^n-2) \end{eqnarray*}

(2)


$\vec{a}=(a_1,\ a_2),\ \ \vec{b}=(b_1,\ b_2)\ \ のとき \quad \vec{a}\cdot \vec{b}=a_1b_1+a_2b_2$

\begin{eqnarray*} & &|\vec{a}|^2 |\vec{b}|^2 -(\vec{a} \cdot \vec{b})^2\\ \\ &=&(a_1^2+a_2^2)(b_1^2+b_2^2)-(a_1b_1+a_2b_2)^2\\ \\ &=&a_1^2b_2^2+a_2^2b_1^2-2a_1a_2b_1b_2\\ \\ &=&(a_1b_2-a_2b_1)^2 \end{eqnarray*}

(3)

　

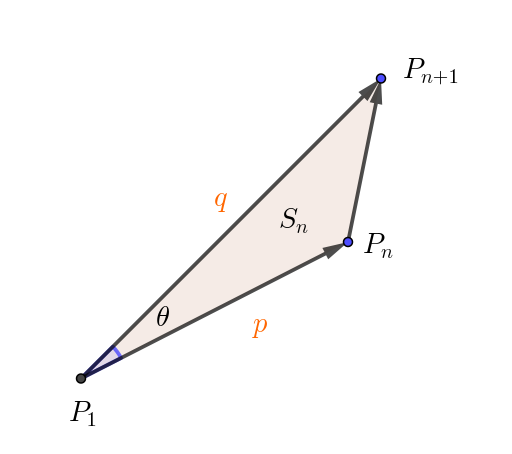
$\vec{P_1P_n}=\vec{p},\ \ |\vec{p}|=p,\quad \vec{P_1P_{n+1}}=\vec{q},\ \ |\vec{q}|=q,\quad \angle P_nP_1P_{n+1}=\theta \quad とおくと$

$(1) より \quad \vec{p}=(p_1,\ p_2)=(n-1,\ 2^n-2),\quad \vec{q}=(q_1,\ q_2)=(n,\ 2^{n+1}-2)$

$\vec{p} \cdot \vec{q}=pq\cos \theta \quad だから$

\begin{eqnarray*} S_n &=&\cfrac{1}{2}pq\sin \theta\\ \\ &=&\cfrac{1}{2}pq\sqrt{1-\cos ^2 \theta}\\ \\ &=&\cfrac{1}{2}pq\sqrt{1-\big(\dfrac{\vec{p} \cdot \vec{q}}{pq}\big)^2}\\ \\ &=&\cfrac{1}{2}\sqrt{p^2q^2-\big(\vec{p} \cdot \vec{q}\big)^2}\\ \\ &=&\cfrac{1}{2}\sqrt{(p_1q_2-p_2q_1)^2}\\ \\ &=&\cfrac{1}{2}|p_1q_2-p_2q_1|\\ \\ &=&\cfrac{1}{2}|(n-1)(2^{n+1}-2)-(2^n-2)n|\\ \\ &=&\cfrac{1}{2}|2(n-1)2^n-2(n-1)-n2^n+2n|\\ \\ &=&\cfrac{1}{2}|n2^n-2\cdot 2^n+2|\\ \\ &=&\cfrac{1}{2}|(n-2)2^n+2|\\ \\ &=&\cfrac{1}{2}\big((n-2)2^n+2\big)\\ \\ &=&(n-2)2^{n-1}+1 \end{eqnarray*}

(4)

　

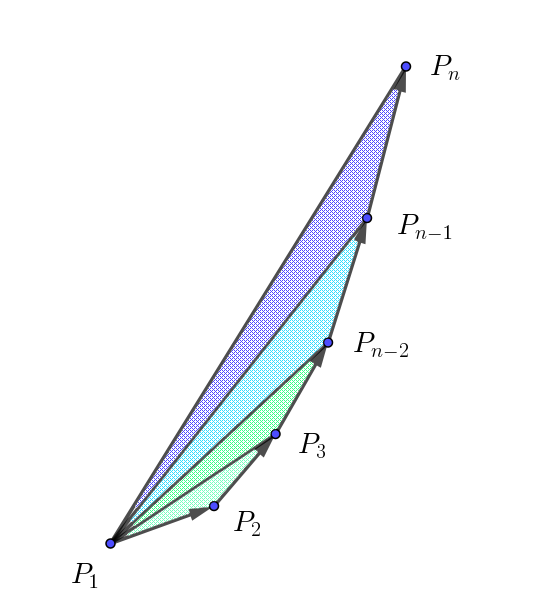
\begin{eqnarray*} T_n &=&S_2+S_3+S_4+ \cdots + S_{n-1}\\ \\ &=&1+(1 \cdot 2^2+1)+(2 \cdot 2^3+1)+ \cdots + ((n-3)2^{n-2}+1)\\ \\ &=&1 \cdot 2^2 + 2 \cdot 2^3 + \cdots + (n-3)2^{n-2}+(n-2)\\ \end{eqnarray*} $U_n=1 \cdot 2^2 + 2 \cdot 2^3 + \cdots + (n-3)2^{n-2} \hspace{3em}とおくと$

$2U_n=\hspace{3em} 1 \cdot 2^3 + \cdots + (n-4)2^{n-2} + (n-3)2^{n-1}$

$辺々引いて$
\begin{eqnarray*} -U_n &=&2^2 + 2^3 + \cdots + 2^{n-2} -(n-3)2^{n-1}\\ \\ &=&\cfrac{2^2(2^{n-3}-1)}{2-1}-(n-3)2^{n-1}\\ \\ &=&2^{n-1}-4-(n-3)2^{n-1}\\ \\ &=&-(n-4)2^{n-1}-4\\ \end{eqnarray*} $\therefore \ \ U_n=(n-4)2^{n-1}+4$

$よって$
\begin{eqnarray*} T_n &=&U_n+(n-2)\\ \\ &=&(n-4)2^{n-1}+4+(n-2)\\ \\ &=&(n-4)2^{n-1}+n+2 \end{eqnarray*}

ページの先頭へ↑



メインメニュー　に戻る