筑波大学(理系) 2025年 問題4
$i\ を虚数単位とする。a\ は \ 1\ でない正の実数の定数とする。複素数平面座標平面において、方程式$
$|z-a^2i|=a|z-i| \ \ を満たす点z\ が表す図形を \ C\ とする。$
$(1)\ \ 図形C\ は原点O\ を中心とする円であることを示し、その半径を求めよ。$
$以下の問いでは点z\ は円C\ 上を動くとし、z\ の偏角を \ \theta \ とする。ただし、0 \leqq \theta < 2\pi \ \ とする。$
$また、w=z-\dfrac{1}{z} \ \ とおく。$
$(2)\ \ |w-2i|^2 \ \ を \ a\ と \ \sin \theta \ \ を用いて表せ。$
$(3)\ \ |w-2i|+|w+2i| \ \ は点z\ の位置によらない定数であることを示せ。$
(1)
$|z-a^2i|=a|z-i| \ \ の両辺を平方して$
$|z-a^2i|^2=a^2|z-i|^2$
$(z-a^2i)(\overline{z}+a^2i)=a^2(z-i)(\overline{z}+i)$
$z\overline{z} +a^4+a^2(z-\overline{z})i =a^2(z\overline{z}+1+(z- \overline{z})i)$
$(a^2-1)z\overline{z} =a^4 - a^2 $
$(a^2-1)|z|^2=a^2(a^2 - 1)$
$(a^2-1)(|z|^2 -a^2)=0$
$(a^2-1)(|z|+a)(|z|-a)=0$
$a \ne 1 , \quad a > 0 \ \ だから \quad a^2-1 \ne0, \quad |z|+a >0 $
$\therefore \ \ |z|=a $
$よって、図形C\ は原点O\ を中心とする半径 \ a\ の円を表す。$
(2)
$(1) より \quad z=a(\cos \theta +i\sin \theta) \quad とおける。$
$設問(3)を考慮し \quad |w \pm 2i|^2 \quad を求める。$
\begin{eqnarray*} & &|w \pm 2i|^2\\ \\ &=&|z-\dfrac{1}{z} \pm 2i|^2\\ \\ &=&|a(\cos \theta +i\sin \theta)-\dfrac{1}{a(\cos \theta +i\sin \theta)} \pm 2i|^2\\ \\ &=&|a(\cos \theta +i\sin \theta)-\dfrac{1}{a}(\cos \theta -i\sin \theta) \pm 2i|^2\\ \\ &=&\big|(a-\dfrac{1}{a})\cos \theta +i\big((a+\dfrac{1}{a})\sin \theta \pm 2 \big) \big|^2\\ \\ &=&(a-\dfrac{1}{a})^2 \cos ^2\theta +\big((a+\dfrac{1}{a}) \sin \theta \pm 2 \big)^2 \\ \\ &=&(a-\dfrac{1}{a})^2 \cos ^2\theta +(a+\dfrac{1}{a})^2 \sin ^2\theta \pm 4(a+\dfrac{1}{a})\sin \theta +4 \\ \\ &=&(a^2+\dfrac{1}{a^2})(\cos ^2\theta + \sin ^2 \theta) -2\cos ^2 \theta +2\sin ^2 \theta \pm 4(a+\dfrac{1}{a})\sin \theta +4 \\ \\ &=&a^2+\dfrac{1}{a^2} -2(\cos ^2 \theta -\sin ^2 \theta) \pm 4(a+\dfrac{1}{a})\sin \theta +4 \\ \\ &=&a^2+\dfrac{1}{a^2} -2(1-2\sin ^2 \theta) \pm 4(a+\dfrac{1}{a})\sin \theta +4 \\ \\ &=&a^2+\dfrac{1}{a^2} +2 +4\sin ^2 \theta \pm 4(a+\dfrac{1}{a})\sin \theta \\ \\ &=&\big(a+\dfrac{1}{a}\big)^2 \pm 4(a+\dfrac{1}{a})\sin \theta +4\sin ^2 \theta \\ \\ &=&\big(a+\dfrac{1}{a} \pm 2\sin \theta \big)^2\\ \end{eqnarray*} $ここで、a+\dfrac{1}{a} \geqq 2 \quad より \quad a+\dfrac{1}{a}\geqq \pm 2\sin \theta \quad \therefore \ \ a+\dfrac{1}{a} \pm 2\sin \theta \geqq 0$
$したがって \quad |w -2i|=a+\dfrac{1}{a} - 2\sin \theta $
(3)
$(2) より \quad |w +2i|=a+\dfrac{1}{a} + 2\sin \theta \quad だから$
$|w-2i|+|w+2i|=\big(a+\dfrac{1}{a} - 2\sin \theta \big)+\big(a+\dfrac{1}{a} + 2\sin \theta \big)=2\big(a+\dfrac{1}{a}\big)$
$よって、|w-2i|+|w+2i|\ \ は点z\ の位置によらない定数である。$
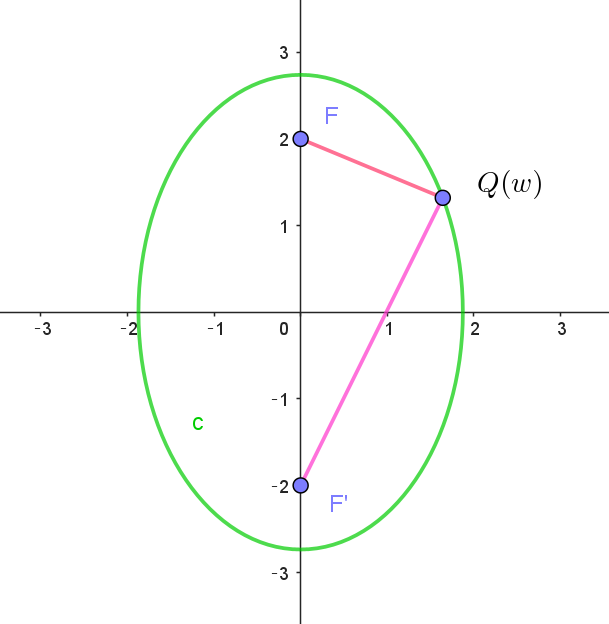
$(2)で求めたように$
$w=z-\dfrac{1}{z}=(a-\dfrac{1}{a})\cos \theta +i(a+\dfrac{1}{a})\sin \theta \quad だから$
$w=x+yi \quad とおくと \quad x=(a-\dfrac{1}{a})\cos \theta ,\quad y=(a+\dfrac{1}{a})\sin \theta $
$\cos \theta=\dfrac{x}{a-\dfrac{1}{a}},\quad \sin \theta=\dfrac{y}{a+\dfrac{1}{a}}$
$cos ^2 \theta + \sin ^2 \theta=1 \quad に代入して$
$\big(\dfrac{x}{a-\dfrac{1}{a}}\big)^2+ \big(\dfrac{y}{a+\dfrac{1}{a}}\big)^2=1$
$\big(a+\dfrac{1}{a}\big)^2-\big(a-\dfrac{1}{a}\big)^2=4 \quad だから \quad \big(a+\dfrac{1}{a}\big)^2 > \big(a-\dfrac{1}{a}\big)^2$
$したがって、複素数平面上で虚軸上に焦点 \ F(0,\ 2),\ \ F'(0,\ -2)\ \ をもつ楕円である。$
$この楕円上の任意の点を \ Q(w)\ とすると、楕円の定義から$
$QF+QF'=2(a+\dfrac{1}{a}) $
$これが、設問(3)の意味するところです。$
メインメニュー に戻る