筑波大学(理系) 2025年 問題3
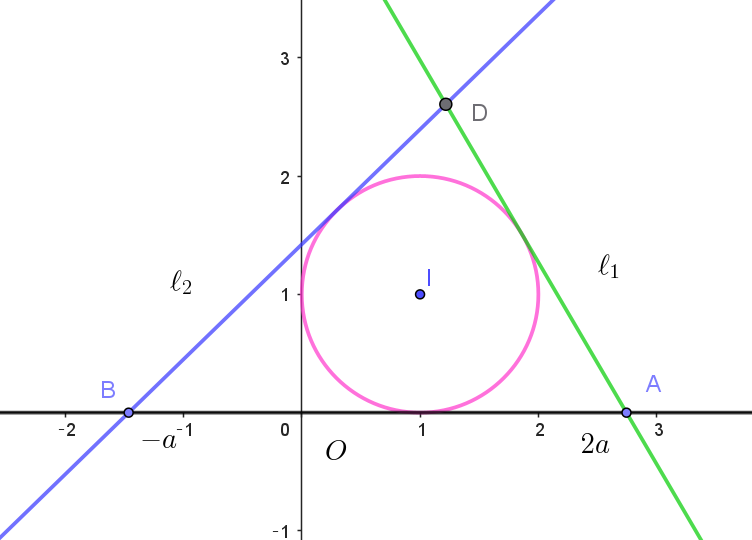
$座標平面において円 \ (x-1)^2+(y-1)^2=1\ \ を \ C\ とする。a\ を \ 1\ より大きい実数とし、2\ 点A(2a,\ 0),$
$B(-a,\ 0)\ \ をとる。点A\ を通る円C\ の \ 2\ 本の接線のうち傾きが小さいほうを \ \ell_1 \ とし、点B\ を通る円C\ の$
$2本の接線のうち傾きが大きいほうを \ \ell_2 \ とする。\ell_1 \ と \ \ell_2 \ の交点をD\ とする。$
$(1)\ \ 直線 \ \ell_1 \ の方程式を \ a\ を用いて表せ。$
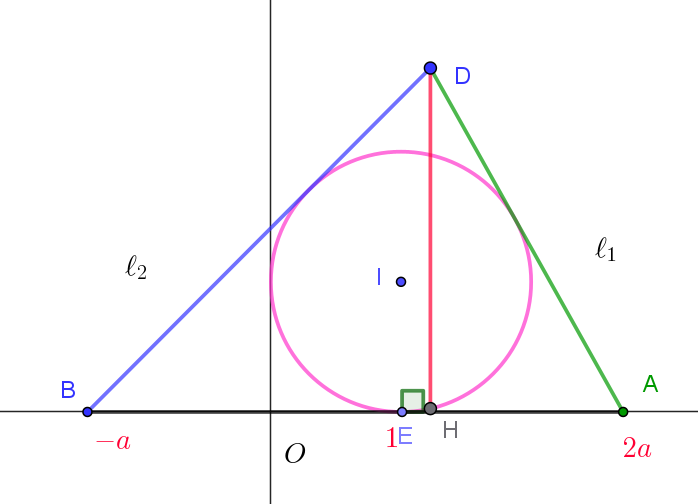
$(2)\ \ 点D\ から \ x\ 軸へ下ろした垂線と \ x\ 軸の交点を \ H\ とする。\triangle BDH \ と \ \triangle ADH \ の面積の比が \ \ 5:4\ \ で$
$\quad あるとき、a\ の値を求めよ。$
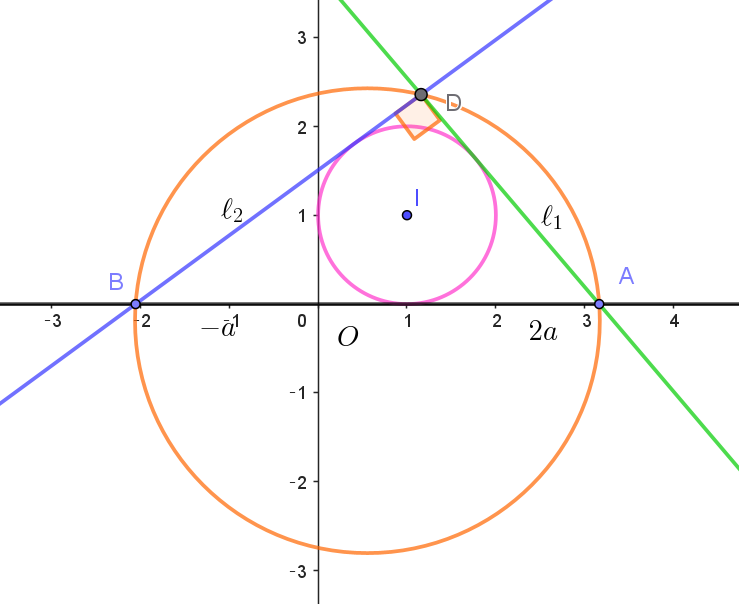
$(3)\ \ a\ が(2)で求めた値であるとき、\angle ADB=\dfrac{\pi}{2} \ \ であることを示せ。また、\triangle ABD \ \ の外接円の中心と$
$\quad 半径を求めよ。$
$直線や円の方程式で求める方法と図形的に求める方法の \ 2\ 通りを示します。$
$前者はどちらかというと少し固いイメージがあり、後者はエレガントな感じがします。$
$(解法Ⅰ)$
(1)
$(x-1)^2+(mx-2ma-1)^2=1$
$(1+m^2)x^2-2\{1+m(2ma+1)\}x+(2ma+1)^2=0$
$接する条件は判別式 \ D\ が$
$\dfrac{D}{4}=\{1+m(2ma+1)\}^2-(1+m^2)(2ma+1)^2=0$
$1+2m(2ma+1)-(2ma+1)^2=0$
$4a(1-a)m^2+2(1-2a)m=0$
$\ell_1 \ の傾きは \ 0\ でないから$
$m=\dfrac{2a-1}{2a(1-a)}=-\dfrac{2a-1}{2a(a-1)}$
$よって \quad \ell_1 : y=-\dfrac{2a-1}{2a(a-1)}(x-2a)$
(2)
$y=-\dfrac{-a-1}{-a(-\dfrac{a}{2}-1)}(x+a)$
$よって \quad \ell_2 : y=\dfrac{2(a+1)}{a(a+2)}(x+a)$
$\ell_1 \ と \ \ell_2 \ の交点D\ の \ x\ 座標は$
$-\dfrac{2a-1}{2a(a-1)}(x-2a)=\dfrac{2(a+1)}{a(a+2)}(x+a)$
$-(a+2)(2a-1)(x-2a)=4(a-1)(a+1)(x+a)$
$(-2a^2-3a+2)x-2a(-2a^2-3a+2)=4(a^2-1)x+4a(a^2-1)$
$(6a^2+3a-6)x=6a^2$
$x=\dfrac{2a^2}{2a^2+a-2}$
$AH=2a-\dfrac{2a^2}{2a^2+a-2}=\dfrac{2a(2a^2+a-2-a)}{2a^2+a-2}=\dfrac{4a(a^2-1)}{2a^2+a-2}$
$BH=\dfrac{2a^2}{2a^2+a-2}+a=\dfrac{a(2a+2a^2+a-2)}{2a^2+a-2}=\dfrac{a(2a^2+3a-2)}{2a^2+a-2}=\dfrac{a(a+2)(2a-1)}{2a^2+a-2}$
$\dfrac{\triangle BDH}{\triangle ADH}=\dfrac{BH}{AH}=\dfrac{a(a+2)(2a-1)}{2a^2+a-2} \times \dfrac{2a^2+a-2}{4a(a^2-1)}=\dfrac{(a+2)(2a-1)}{4(a^2-1)}$
$\triangle BDH : \triangle ADH =5:4\ \ だから$
$\dfrac{(a+2)(2a-1)}{4(a^2-1)}=\dfrac{5}{4}$
$(a+2)(2a-1)=5(a^2-1)$
$3a^2-3a-3=0$
$a^2-a-1=0$
$a > 1 \ \ だから \quad a=\dfrac{1+\sqrt{5}}{2}$
(3)
\begin{eqnarray*} & &(\ell_1 \ の傾き) \times (\ell_2 \ の傾き)\\ \\ &=&-\dfrac{2a-1}{2a(a-1)} \times \dfrac{2(a+1)}{a(a+2)}\\ \\ &=&-\dfrac{2a^2+a-1}{a^2(a^2+a-2)}\\ \\ &=&-\dfrac{2(a+1)+a-1}{(a+1)(a+1+a-2)}\\ \\ &=&-\dfrac{3a+1}{2a^2+a-1}\\ \\ &=&-\dfrac{3a+1}{2(a+1)+a-1}\\ \\ &=&-1 \end{eqnarray*} $よって \quad \ell_1 \perp \ell_2 \quad すなわち \quad \angle ADB=\dfrac{\pi}{2}$
$また、\angle ADB=\dfrac{\pi}{2} \quad だから円周角の定理より$
$線分AB\ は外接円の直径である。$
$したがって \quad 半径=\dfrac{2a+a}{2}=\dfrac{3}{2}a=\dfrac{3}{2} \times \dfrac{1+\sqrt{5}}{2}=\dfrac{3}{4}(1+\sqrt{5})$
$中心の \ x\ 座標=2a-\dfrac{3}{2}a=\dfrac{1}{2}a=\dfrac{1}{2} \times \dfrac{1+\sqrt{5}}{2}=\dfrac{1}{4}(1+\sqrt{5})$
$よって 中心は \ \ (\dfrac{1}{4}(1+\sqrt{5}),\ 0)$
$(解法Ⅱ)$
(1)
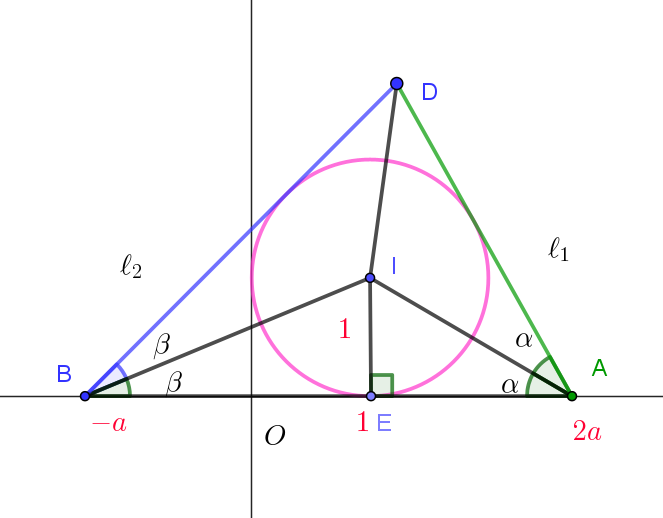
$したがって中心I\ は、3つの内角の二等分線の交点である。$
$\angle DAI=\angle BAI=\alpha,\quad \angle DBI=\angle ABI=\beta \quad とおく$
$円C\ と \ x\ 軸の接点を \ E\ とおく$
$\triangle AIE \ \ は直角三角形だから$
$\tan \alpha=\dfrac{IE}{AE}=\dfrac{1}{2a-1}$
$\tan 2\alpha=\dfrac{2\tan \alpha}{1-\tan ^2\alpha}=\dfrac{\dfrac{2}{2a-1}}{1-\big(\dfrac{1}{2a-1}\big)^2}=\dfrac{2(2a-1)}{(2a-1)^2-1}=\dfrac{2a-1}{2a(a-1)}$
$接線 \ell_1 の傾き=\tan(\pi-2\alpha)=-\tan 2\alpha=-\dfrac{2a-1}{2a(a-1)} \quad だから$
$\ell_1 : y=-\dfrac{2a-1}{2a(a-1)}(x-2a)$
(2)
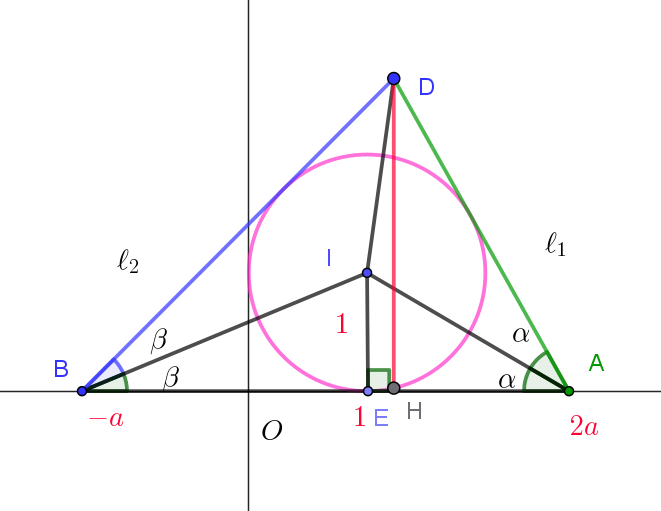
$\tan \beta=\dfrac{IE}{BE}=\dfrac{1}{a+1}$
$\tan 2\beta=\dfrac{2\tan \beta}{1-\tan ^2\beta}=\dfrac{\dfrac{2}{a+1}}{1-\big(\dfrac{1}{a+1}\big)^2}=\dfrac{2(a+1)}{(a+1)^2-1}=\dfrac{2(a+1)}{a(a+2)}$
$直角三角形 ADH \ \ と \ BDH \ \ において$
$DH=AH\tan 2\alpha =BH\tan 2\beta \quad だから$
$\dfrac{\triangle BDH}{\triangle ADH}=\dfrac{BH}{AH}=\dfrac{\tan 2\alpha}{\tan 2\beta}=\dfrac{2a-1}{2a(a-1)} \times \dfrac{a(a+2)}{2(a+1)}=\dfrac{(2a-1)(a+2)}{4(a+1)(a-1)}$
$以下同じ$
(3)
\begin{eqnarray*} \tan(\alpha + \beta) &=&\dfrac{\tan \alpha +\tan \beta}{1-\tan \alpha \tan\beta}\\ \\ &=&\dfrac{\dfrac{1}{2a-1}+\dfrac{1}{a+1}}{1-\dfrac{1}{2a-1} \times \dfrac{1}{a+1}}\\ \\ &=&\dfrac{(a+1)+(2a-1)}{(2a-1)(a+1)-1}\\ \\ &=&\dfrac{3a}{2a^2+a-2}\\ \\ &=&\dfrac{3a}{2(a+1)+a-2}\\ \\ &=&\dfrac{3a}{3a}\\ \\ &=&1 \end{eqnarray*} $0 < \alpha +\beta <\pi \quad だから \quad \alpha + \beta =\dfrac{\pi}{4}$$\therefore \ \ \angle ADB=\pi -2(\alpha + \beta)=\dfrac{\pi}{2}$
$以下同じ$
メインメニュー に戻る