筑波大学(理系) 2025年 問題2
$正の実数 \ p\ に対して、f(x)=x^3-x+p \ \ とする。$
$(1)\ \ x\ につての方程式 \ \ f(x)=0 \ \ がただ \ 1\ つの実数解をもつとき 、p\ のとりうる値の範囲を求めよ。$
$(2)\ \ a,\ b,\ c\ は実数で \ c > 0 \ とする。また、i\ を虚数単位とする。a,\ \ b+ci,\ \ b-ci \ \ が方程式 \ f(x)=0$
$\quad の解であるとき、a,\ c,\ p\ をそれぞれ \ b\ を用いて表し、b\ のとりうる値の範囲を求めよ。$
$(3)\ \ (2)の \ b,\ \ c\ について、少なくともどちらか一方は整数でないことを示せ。$
(1)
$f'(x)=3x^2-1 \quad f'(x)=0 \ \ より \quad x=\pm \dfrac{1}{\sqrt{3}}$
\[ \begin{array}{c||c|c|c|c|c} x& \cdots & -\dfrac{1}{\sqrt{3}} & \cdots & \dfrac{1}{\sqrt{3}} & \cdots\\ \hline f'(x)& + & 0 & - & 0 & + \\ \hline f(x)& \nearrow & 極大 & \searrow & 極小 & \nearrow\\ \end{array} \]
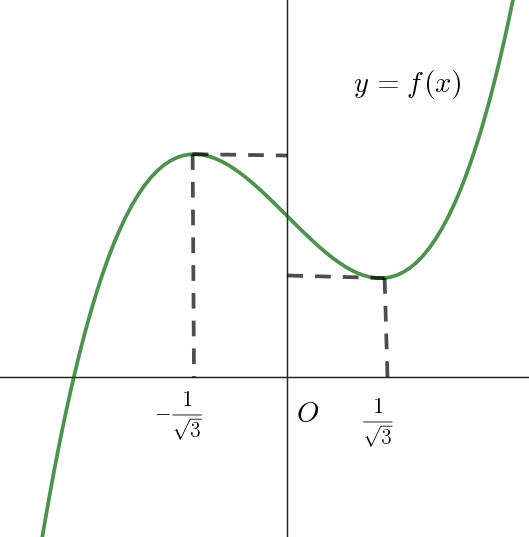
$x=-\cfrac{1}{\sqrt{3}}\ で極大となり、極大値は$
$f(-\cfrac{1}{\sqrt{3}})=-\dfrac{1}{3\sqrt{3}} + \dfrac{1}{\sqrt{3}} +p=p+\dfrac{2}{3\sqrt{3}} > 0$
$x=\cfrac{1}{\sqrt{3}}\ で極小となり、極小値は$
$f(\cfrac{1}{\sqrt{3}})=\dfrac{1}{3\sqrt{3}} - \dfrac{1}{\sqrt{3}} +p=p-\dfrac{2}{3\sqrt{3}}$
$f(x)=0 \ \ がただ \ 1\ つの実数解をもつような \ y=f(x)\ のグラフは右図の場合であるから$
$極小値が正であればよい。$
$よって \quad p-\dfrac{2}{3\sqrt{3}} > 0 \quad \therefore \ \ p > \dfrac{2}{3\sqrt{3}}$
(2)
$f(x)=x^3-x+p=0 \ \ の解が \quad a,\ \ b+ci,\ \ b-ci \ \ だから解と係数の関係より$
(i)$\ \ a + (b+ci)+(b-ci)=0 \qquad \therefore \ \ a=-2b$
(ii)$\ \ a(b+ci)+(b+ci)(b-ci)+a(b-ci)=-1$
$\quad 2ab+b^2+c^2=-1$
$\quad a=-2b \quad を代入して \quad -4b^2+b^2+c^2=-1$
$\quad c^2=3b^2-1 \qquad c > 0 \quad だから \quad c=\sqrt{3b^2-1}$
(iii)$\ \ a (b+ci)(b-ci)=-p$
$\quad a(b^2+c^2)=-p$
$\quad p=-(-2b)\big(b^2+(3b^2-1)\big)=2b(4b^2-1)=2b(2b+1)(2b-1)$
$また、b\ のとりうる値の範囲は$
$\ \ c^2=3b^2-1 > 0 \quad より \quad b^2 > \dfrac{1}{3} \qquad b < -\dfrac{1}{\sqrt{3}}, \quad \dfrac{1}{\sqrt{3}} < b$
$p=2b(2b+1)(2b-1) > 0 \quad より \quad -\dfrac{1}{2} < b < 0 ,\quad \dfrac{1}{2} < b$
$ともに満たす \ b\ の範囲は \quad b > \dfrac{1}{\sqrt{3}} $
(3)
$(2)より \quad 3b^2 -c^2=1 \quad だから \quad Q=3b^2-c^2 \quad とおく。$
$b,\ c\ \ がともに整数とすると、次の \ 4\ 通りのパターンがある。$
(i)$\ \ b\ は偶数、c\ は偶数のとき$
$\quad b=2k,\ \ c=2m \ \ (k,\ m \ は整数)\quad とおくと$
$\quad Q=3(2k)^2-(2m)^2=4(3k^2-m^2) \quad だから\ Q\ は偶数となり、右辺は奇数 \ 1\ だから不合理$
(ii)$\ \ b\ は偶数、c\ は奇数のとき$
$\quad b=2k,\ \ c=2m-1 \quad とおくと$
$\quad Q=3(2k)^2-(2m-1)^2=4(3k^2-m^2+m-1)+3 \quad だからこれが右辺の \ 1\ に一致することはない。$
(iii)$\ \ b\ は奇数、c\ は偶数のとき$
$\quad b=2k-1,\ \ c=2m \quad とおくと$
$\quad Q=3(2k-1)^2-(2m)^2=4(3k^2-3k-m^2)+3 \quad だからこれが右辺の \ 1\ に一致することはない。$
(iv)$\ \ b\ は奇数、c\ は奇数のとき$
$\quad b=2k-1,\ \ c=2m-1 \quad とおくと$
$\quad Q=3(2k-1)^2-(2m-1)^2=4(3k^2-3k-m^2+m)+2 \quad だから \ Q\ は偶数となり、右辺は奇数 \ 1\ だから不合理$
$よって、b,\ c\ がともに整数であることはないから、少なくともどちらか一方は整数でない。$
メインメニュー に戻る