筑波大学(理系) 2024年　問題6


$定数 \ \alpha \ は実数でない複素数とする。以下の問いに答えよ。$
$(1)\ \ \dfrac{\alpha - |\alpha|}{\alpha + |\alpha |} \ \ は純虚数であることを示せ。$
$(2)\ \ 純虚数 \ \beta \ で、\dfrac{\beta - |\alpha|}{\alpha + |\alpha |} \ \ が純虚数となるものがただ一つ存在することを示せ。$
$(3)\ \ 複素数\ z\ を \ \ \dfrac{z - |\alpha|}{\alpha + |\alpha |}\ \ が純虚数となるように動かすとき、|z|\ が最小となる \ z\ を \ \alpha \ を用いて表せ。$


(1)


$w=\dfrac{\alpha - |\alpha|}{\alpha + |\alpha |} \ \ とおくと$

\begin{eqnarray*} & &w+\overline{w}\\ \\ &=&\dfrac{\alpha - |\alpha|}{\alpha + |\alpha |} + \dfrac{\overline{\alpha} - |\alpha|}{\overline{\alpha} + |\alpha |}\\ \\ &=&\dfrac{(\alpha - |\alpha|)(\overline{\alpha} + |\alpha|)+ (\overline{\alpha} - |\alpha|)(\alpha + |\alpha|)}{(\alpha + |\alpha|)(\overline{\alpha}+|\alpha|)}\\ \\ &=&\dfrac{(|\alpha|^2 + \alpha |\alpha| -\overline{\alpha} |\alpha| -|\alpha|^2)+ (|\alpha|^2 + \overline{\alpha}|\alpha| - \alpha |\alpha| - |\alpha|^2 )}{(\alpha + |\alpha|)(\overline{\alpha}+|\alpha|)}\\ \\ &=&0 \end{eqnarray*}
$したがって \quad w=\dfrac{\alpha - |\alpha|}{\alpha + |\alpha |} \ \ は純虚数である。$


$(別解)$

　

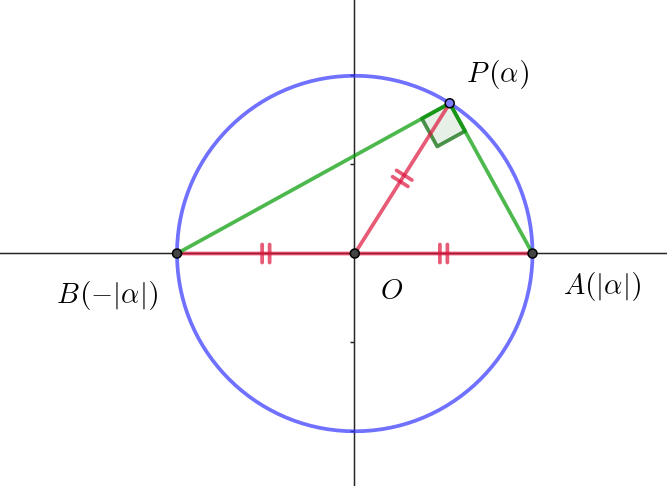
$|\alpha| \ は実数だから、複素数平面の実軸上にA(|\alpha|),\ \ B(-|\alpha|)\ \ をとり$

$右図のように \ \ P(\alpha)\ \ をとる。$

$OP=OA=OB \ \ だから \ 3\ 点 \ P,\ A,\ B\ は原点中心、$

$半径 \ \ |\alpha| \ \ の円周上にある。$

$円周角の定理より \quad \angle APB=90°\quad だから \quad AP \perp BP$

$よって \quad \alpha -|\alpha|\ \ と \ \ \alpha +|\alpha|\ \ の偏角の差は \ 90°\ だから$

$\dfrac{\alpha - |\alpha|}{\alpha + |\alpha |} \ \ は純虚数である。$


(2)


$\beta \ は純虚数だから \quad \overline{\beta}=-\beta $

$w=\dfrac{\beta - |\alpha|}{\alpha + |\alpha |} \ \ とおくと$

\begin{eqnarray*} & &w+\overline{w}\\ \\ &=&\dfrac{\beta - |\alpha|}{\alpha + |\alpha |} + \dfrac{\overline{\beta} - |\alpha|}{\overline{\alpha} + |\alpha |}\\ \\ &=&\dfrac{\beta - |\alpha|}{\alpha + |\alpha |} + \dfrac{- \beta - |\alpha|}{\overline{\alpha} + |\alpha |}\\ \\ &=&\dfrac{(\beta - |\alpha|)(\overline{\alpha} + |\alpha|) - (\beta + |\alpha|)(\alpha + |\alpha|)}{(\alpha + |\alpha|)(\overline{\alpha}+|\alpha|)}\\ \\ &=&\dfrac{(\overline{\alpha} \beta + \beta |\alpha| -\overline{\alpha} |\alpha| -|\alpha|^2) - (\alpha \beta + \beta |\alpha| + \alpha |\alpha| + |\alpha|^2 )}{(\alpha + |\alpha|)(\overline{\alpha}+|\alpha|)}\\ \\ &=&\dfrac{-(\alpha - \overline{\alpha}) \beta - \alpha |\alpha| - \overline{\alpha} |\alpha| -2|\alpha |^2 }{(\alpha + |\alpha|)(\overline{\alpha}+|\alpha|)}\\ \end{eqnarray*}
$w=\dfrac{\beta - |\alpha|}{\alpha + |\alpha |} \ \ が純虚数だから \quad w+\overline{w}=0$

$よって$

$-(\alpha - \overline{\alpha}) \beta - \alpha |\alpha| - \overline{\alpha} |\alpha| -2|\alpha |^2 =0$

\begin{eqnarray*} \beta &=&- \cfrac{ \alpha |\alpha| + \overline{\alpha} |\alpha| + 2|\alpha |^2}{\alpha - \overline{\alpha}}\\ \\ &=&- \cfrac{ (\alpha + \overline{\alpha} + 2|\alpha |)|\alpha |}{\alpha - \overline{\alpha}}\\ \\ &=&- \cfrac{ (\alpha + \overline{\alpha} + 2|\alpha |)|\alpha | \times (\overline{\alpha} - \alpha )}{|\alpha - \overline{\alpha}|^2}\\ \\ &=&\cfrac{ (\alpha + \overline{\alpha} + 2|\alpha |)|\alpha | \times (\alpha - \overline{\alpha} )}{|\alpha - \overline{\alpha}|^2}\\ \end{eqnarray*}
$ここで、分母は実数、分子 \ \ \alpha + \overline{\alpha} \ \ は実数、\alpha - \overline{\alpha} \ \ は純虚数だから分子は純虚数$

$純虚数 \ \ \beta \ で、w \ が純虚数となるものがただ一つ存在する。$


$(別解)$

　

$(1)の別解で示したように \quad AP \perp BP$

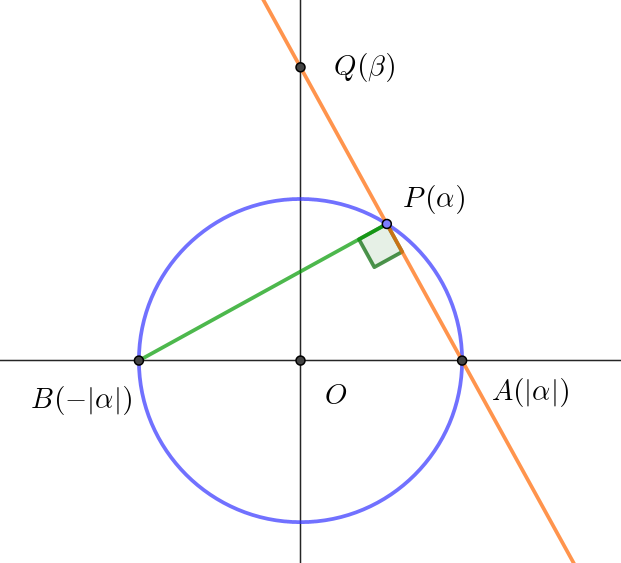
$線分 \ AP\ を延長して、虚軸との交点を \ Q(\beta)\ とする。$

$\alpha \ は実数でない複素数だから$

$AP /\!/ 虚軸 となることはないので、交点 \ Q\ は必ず存在する。$

$このとき、AQ \perp BP \quad だから$

$純虚数 \ \beta \ で、\dfrac{\beta - |\alpha|}{\alpha + |\alpha |} \ \ が純虚数となるものがただ一つ存在する。$

$なお、\beta \ \ を求めるには解答のようにする。$


(3)

　

$複素数 \ z\ の表す点をR(z),\ \ 直線 \ AP\ を \ \ell \ \ とおく。$

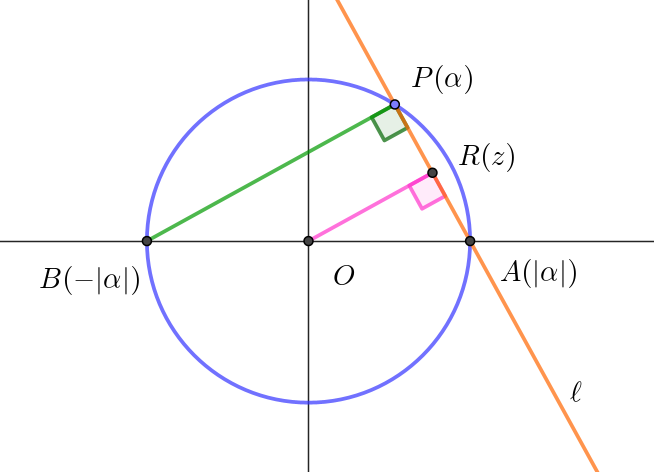
$\dfrac{z - |\alpha|}{\alpha + |\alpha |} \ \ は純虚数だから \quad AR \perp BP $

$よって、R(z)\ は直線 \ \ell \ 上の点である。$

$|z|\ は原点 \ O\ と \ R(z)\ の距離だから、これが最小となる点は$

$\vec{OR}\ が \ \ell \ に垂直なときである。$

$OR /\!/ BP \ \ だから \quad \vec{OR}=k\vec{BP}\ \ (k\ は実数)\ \ とおける。$

$したがって \quad z=k(\alpha + |\alpha|) $

$また$

$\triangle OAR \sim \triangle BAP \quad より$

$OR : BP=OA : BA=1:2$

$OR=\cfrac{1}{2}BP$

$したがって \quad |z|\ が最小となる \ z\ は \quad z=\cfrac{1}{2}(\alpha + |\alpha)) $


ページの先頭へ↑




メインメニュー　に戻る