筑波大学(理系) 2024年　問題5


\[a\ と \ b\ は実数の定数とする。関数 \ \ f(x)=(1-2x^2)\cos 2x +2x\sin 2x +a\cos ^2x +b\int_0^x t\sin 2tdt \quad について、\] $以下の問いに答えよ。$
$(1)\ \ a=8\pi^2,\ \ b=-4\pi \ \ のとき、 0 < x < \dfrac{3}{2}\pi \ \ において \ f(x)\ が極値をとる \ x\ の値をすべて求めよ。$
$(2)\ \ 次の条件(B)を満たす \ a,\ b\ を求めよ。$
$\qquad (B) \quad 0 < x < \dfrac{3}{2}\pi \ \ において、f(x)\ は極値をとらない。$


(1)


\[関数 \ \ f(x)=(1-2x^2)\cos 2x +2x\sin 2x +a\cos ^2x +b\int_0^x t\sin 2tdt \quad より\] \begin{eqnarray*} f'(x) &=&-4x\cos 2x -2(1-2x^2)\sin 2x +2\sin 2x +4x\cos 2x -2a\cos x \sin x +bx\sin 2x\\ \\ &=&4x^2\sin2x -a\sin 2x +bx\sin 2x\\ \\ &=&(4x^2 + bx -a )\sin 2x \end{eqnarray*}
$ここで、a=8\pi^2,\quad b=-4\pi \quad だから$

\begin{eqnarray*} f'(x) &=&(4x^2 - 4\pi x -8\pi ^2 )\sin 2x \\ \\ &=&4(x^2 - \pi x -2\pi ^2 )\sin 2x \\ \\ &=&4(x+\pi )(x- 2\pi) \sin 2x \\ \end{eqnarray*}
$0 < x < \dfrac{3}{2}\pi \quad だから \quad x+\pi >0 , \quad x- 2\pi < 0$

$f'(x)=0 \quad より \quad \sin 2x=0$

$0 < 2x < 3\pi \ \ の範囲で \quad 2x=\pi,\quad 2\pi$

$\therefore \ \ x=\cfrac{\pi}{2},\quad \pi$

$増減表$
\[ \begin{array}{c||c|c|c|c|c} x& 0 & \cdots & \dfrac{\pi}{2} & \cdots & \pi & \cdots & \dfrac{3}{2}\pi\\ \hline f'(x)& & - & 0 & + & 0 & - & \\ \hline f(x))& & \searrow & 極小 & \nearrow & 極大 & \searrow\\ \end{array} \]
$よって \quad x=\cfrac{\pi}{2},\quad \pi \quad で極値をとる。$


(2)

　

$(1)より \quad f'x)=(4x^2 + bx -a )\sin 2x $

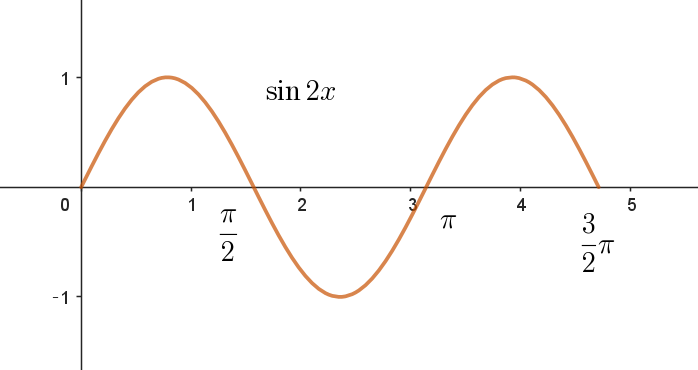
$0 < x < \dfrac{3}{2}\pi \ \ で \ \ \sin 2x \ \ のグラフは右図のとおり$

$したがって \quad 　g(x)=4x^2+bx-a \quad の符号が$
\[ \begin{array}{c||c|c|c|c|c} x& 0 & \cdots & \dfrac{\pi}{2} & \cdots & \pi & \cdots & \dfrac{3}{2}\pi\\ \hline g(x)& & + & 0 & - & 0 & + & \\ \end{array} \]

　

$であれば、0 < x < \dfrac{3}{2}\pi \ \ で \ \ f'(x) > 0 \ \ となり極値をとらない。$

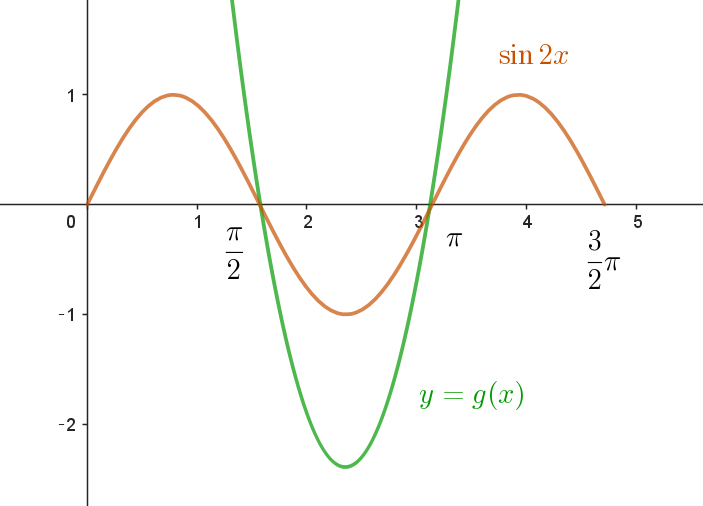
$このとき \ 2\ 次関数 \ \ y=g(x)\ \ のグラフは右図のとおりで、$

$x\ 軸と \ \ \cfrac{\pi}{2},\ \ \cfrac{3}{2}\pi \quad で交わるから$

$y=4(x-\cfrac{\pi}{2})(x-\cfrac{3}{2}\pi) $

$y=4x^2-6\pi x +2\pi ^2$

$よって \quad a=-2\pi ^2, \quad b=-6\pi$


ページの先頭へ↑




メインメニュー　に戻る