筑波大学(理系) 2024年　問題4


$座標平面において、媒介変数表示 \ \ x=-t(t-\dfrac{3}{2}),\ \ y=\sin \pi t \ \ (0 \leqq t \leqq 1)\ \ で表される曲線を \ C\ とする。$
$以下の問いに答えよ。$
\[(1)\ \ 定積分 \ \ \int _0^1 t\sin \pi t dt \ \ を求めよ。\] $(2)\ \ 変数 \ a\ に対し、曲線 \ C\ と直線 \ x=a\ の共有点の個数を求めよ。$
$(3)\ \ 曲線 \ C\ と \ x\ 軸で囲まれた図形の面積を求めよ。$


$\qquad ＊媒介変数表示の図形の面積を求める問題は($2023年度神戸(理系)問題5$)でも出題されています。$

(1)


\begin{eqnarray*} I &=&\int _0^1 t\sin \pi t dt \\ \\ &=&\big[-\dfrac{1}{\pi}t\cos \pi t \big]_0^1 + \int _0^1 \dfrac{1}{\pi} \cos \pi t dt\\ \\ &=&\dfrac{1}{\pi} + \dfrac{1}{\pi ^2}\big[\sin \pi t\big]_0^1\\ \\ &=&\dfrac{1}{\pi}\\ \end{eqnarray*}

(2)


$x=-t(t-\dfrac{3}{2})=-t^2+\dfrac{3}{2}t \quad において $

$\dfrac{dx}{dt}=-2t+\dfrac{3}{2}=-2(t-\dfrac{3}{4})=0 \quad より \quad t=\dfrac{3}{4}$

$y=\sin \pi t \quad において $

$\dfrac{dy}{dt}=\dfrac{1}{\pi} \cos \pi t=0 \quad より \quad t=\dfrac{1}{2}$

　

$x,y\ の増減表は$
\[ \begin{array}{c||c|c|c|c|c} t & 0 & \cdots & \dfrac{1}{2} & \cdots & \dfrac{3}{4} & \cdots & 1\\ \hline \small{\cfrac{dx}{dt}} & & + & + & + & 0 & - & \\ \hline \small{\cfrac{dy}{dt}} & & + & 0 & - & - & - & \\ \hline x & 0 & \nearrow & \dfrac{1}{2} & \nearrow & \dfrac{9}{16} & \searrow & \cfrac{1}{2}\\ \hline y & 0 & \nearrow & 極大 & \searrow & \dfrac{\sqrt{2}}{2} & \searrow & 0 \\ \end{array} \]
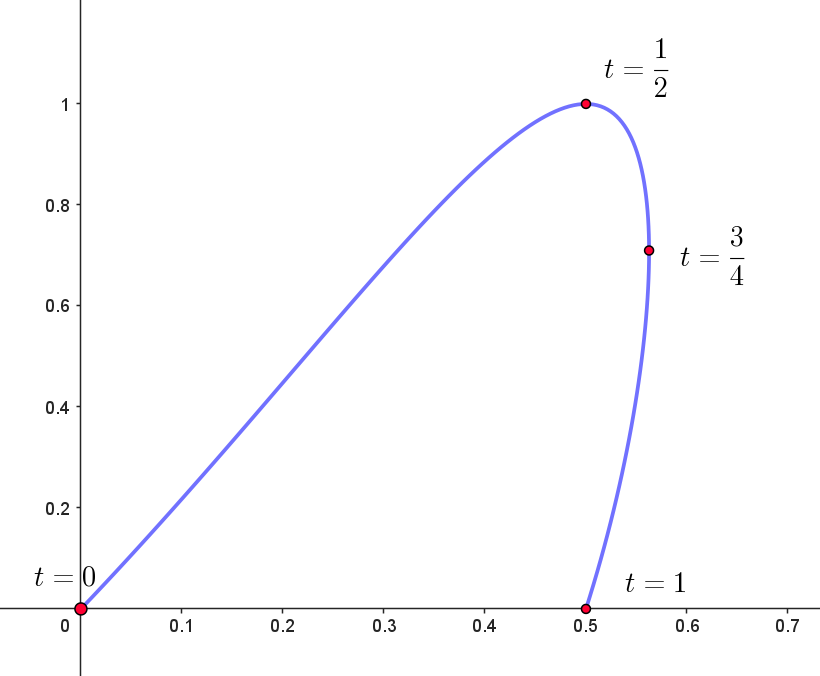
$Cのグラフは右図のとおり$

　

$曲線 \ C\ と直線 \ x=a \ の共有点の個数は$

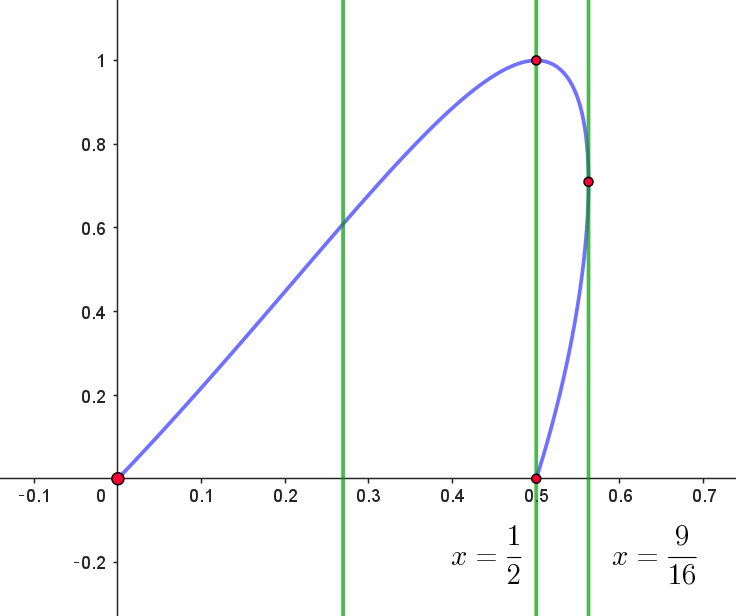
(i)$\ \ a < 0 \quad のとき \hspace{7em} 0\ 個$

(ii)$\ \ 0 \leqq a < \dfrac{1}{2} \quad のとき \hspace{4.5em} 1\ 個$

(iii)$\ \ \dfrac{1}{2} \leqq a < \dfrac{9}{16} \quad のとき \hspace{3em} 2\ 個$

(iv)$\ \ a = \dfrac{9}{16} \quad のとき \hspace{5.5em} 1\ 個$

(v)$\ \ a > \dfrac{9}{16} \quad のとき \hspace{6em} 0\ 個$


(3)

　

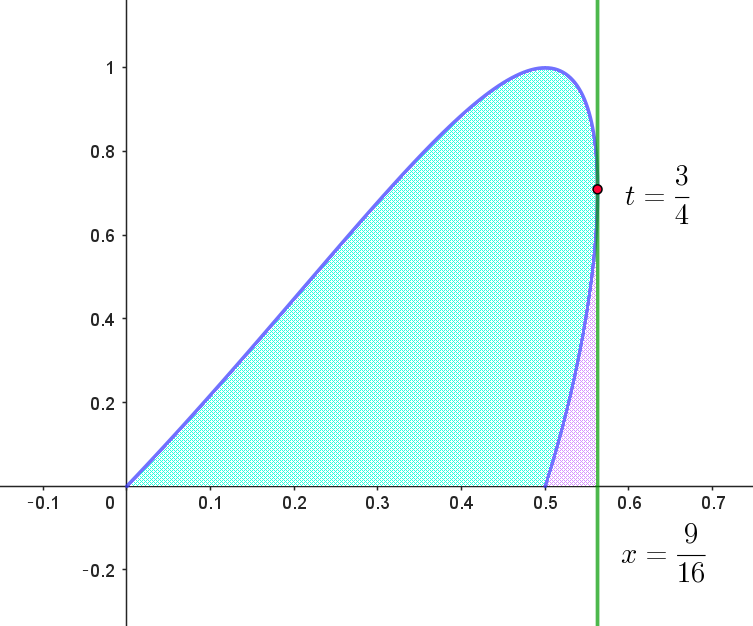
$(2)で求めたように、\dfrac{1}{2} \leqq a < \dfrac{9}{16} \ \ のとき 曲線 \ C\ と直線 \ x=a \ の$

$共有点の個数は \ 2\ 個ある(1\ つの \ x\ に対して \ y\ は \ 2\ 個ある(2\ 価関数$

$といいます))が、どちらの \ y\ をとるかは媒介変数 \ t\ によって定まる。$

$求める図形の面積を \ S\ とおくと$
\begin{eqnarray*} S &=&\int_0^{\scriptsize{\dfrac{9}{16}}}ydx - \int_ {\scriptsize{\dfrac{1}{2}}}^{\scriptsize{\dfrac{9}{16}}}ydx \\ \\ &=&\int_0^{\scriptsize{\dfrac{3}{4}}} \sin \pi t(-2t+\dfrac{3}{2})dt - \int_ 1^{\scriptsize{\dfrac{3}{4}}}\sin \pi t(-2t+\dfrac{3}{2})dt \\ \\ &=&\int_0^1 \sin \pi t(-2t+\dfrac{3}{2})dt \\ \\ &=&-2\int_0^1 t \sin \pi tdt + \dfrac{3}{2}\int_0^1 \sin \pi tdt \\ \\ &=&-2\int_0^1 t \sin \pi tdt + \dfrac{3}{2}\big[- \cfrac{\cos \pi t}{\pi}\big]_0^1 \hspace{5em}(第 \ 1\ 項は(1) より)\\ \\ &=&-\cfrac{2}{\pi} + \cfrac{3}{2}\big(\cfrac{1}{\pi}+\cfrac{1}{\pi}\big)\\ \\ &=&\cfrac{1}{\pi} \end{eqnarray*}

ページの先頭へ↑




メインメニュー　に戻る