筑波大学(理系) 2024年　問題3


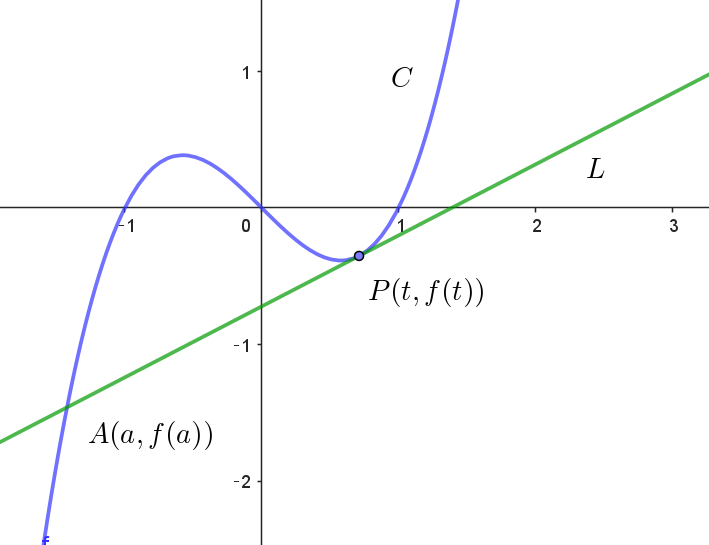
$f(x)=x(x+1)(x-1)\ とする。座標平面において、曲線 \ y=f(x)\ を \ C\ とし、曲線 \ C\ 上の点(t,\ f(t))\ に$
$おける接線を \ L\ とする。以下の問いに答えよ。$
$(1)\ \ 直線 \ L\ の方程式を \ t\ を用いて表せ。$
$(2)\ \ t \ne 0 \ のとき、直線 \ L\ と曲線 \ C\ の共有点で、点(t,\ f(t))\ とは異なるものを \ (a,\ f(a))\ とする。$
$\quad a\ を \ t\ を用いて表せ。また、t\ が \ 0\ を除いた実数を動くとき、f'(t)f'(a)\ の最小値を求めよ。$
$(3)\ \ 次の条件 \ (A)\ をみたすような実数 \ t\ の範囲を求めよ。$
$\quad (A)\ 曲線 \ C\ 上の点(s,\ f(s))\ における接線が直線 \ L\ と直交するような実数 \ s\ が存在する。$


(1)

　

$f(x)=x(x+1)(x-1=x^3-x \quad より \quad f'(x)=3x^2-1$

$接線 \ L\ は \quad y=(3t^2-1)(x-t)+t^3-t$

$L: y=(3t^2-1)x-2t^3$


(2)


$直線 \ L\ と曲線 \ C\ の共有点は$

$x^3-x=(3t^2-1)x-2t^3 \quad の解である。$

$x^3 - 3t^2 x+2t^3 =0$

$x=t \ で接するから \ \ (x-t)^2 \ \ を因数にもつことを考慮して$

$(x-t)^2(x+2t)=0$

$x=t \ \ とは異なるから \quad a=-2t$


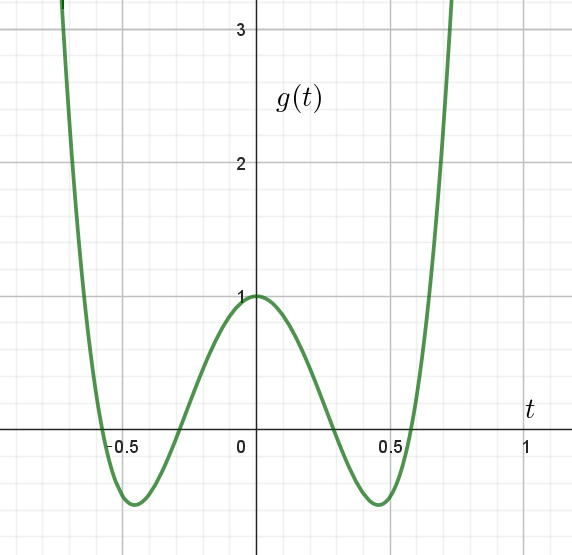
$f'(t)f'(a)=g(t) \quad とおくと$

\begin{eqnarray*} g(t) &=&(3t^2-1)(3a^2-1)\\ \\ &=&(3t^2-1)(12t^2-1)\\ \\ &=&36t^4-15t^2+1\\ \\ \end{eqnarray*} $g'(t)=144t^3-30t=6t(24t^2-5)$

$g'(t)=0 \quad より \quad t \ne 0 \ \ だから \quad t^2=\cfrac{5}{24}$

$t=\pm \cfrac{\sqrt{5}}{2\sqrt{6}}=\pm \cfrac{\sqrt{30}}{12}$

$G(t)\ は偶関数だから \quad t \geqq 0 \quad で考えると$

　

$増減表$
\[ \begin{array}{c||c|c|c|c|c} t& 0 & \cdots & \cfrac{\sqrt{30}}{12} & \cdots \\ \hline g'(t)& & - & 0 & + \\ \hline g(t)& 1 & \searrow & 極小 & \nearrow \\ \end{array} \]
$t= \cfrac{\sqrt{30}}{12}\ で \ g(t)\ は極小かつ最小となり、最小値は$

$g(\cfrac{\sqrt{30}}{12})=(3 \times \cfrac{5}{24}-1)(12 \times \cfrac{5}{24}-1)=-\cfrac{9}{16}$

$よって \quad f'(t)f'(a) \ \ の最小値は \quad t= \pm \cfrac{\sqrt{30}}{12} \quad のとき \quad -\cfrac{9}{16} \quad をとる$


(3)


　

$P(t,\ f(t)),\ \ Q(s,\ f(s))\quad とおくと$

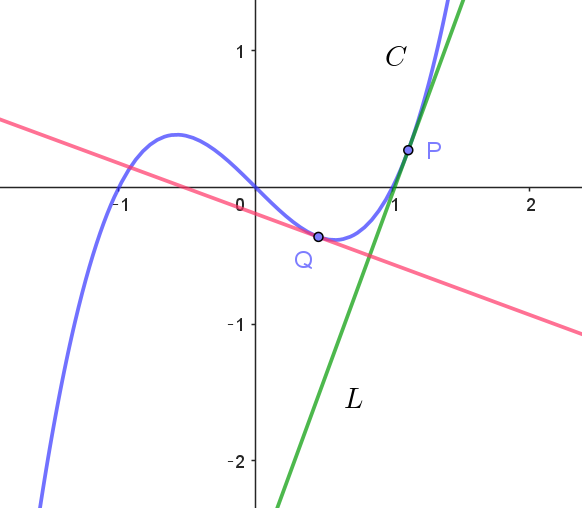
$点P,\ Q\ におけるそれぞれの接線が直交するから$

$(3t^2-1)(3s^2-1)=-1$

$3s^2-1=-\cfrac{1}{3t^2-1}$

$3s^2=1 -\cfrac{1}{3t^2-1} =\cfrac{3t^2-2}{3t^2-1} \geqq 0$

$これを満たす \ t\ は \quad (3t^2-2)(3t^2-1) \geqq 0$

$左辺のグラフは右図のとおりで、不等式の解は$

　

$3t^2-1 \ne 0 \ \ に注意して$

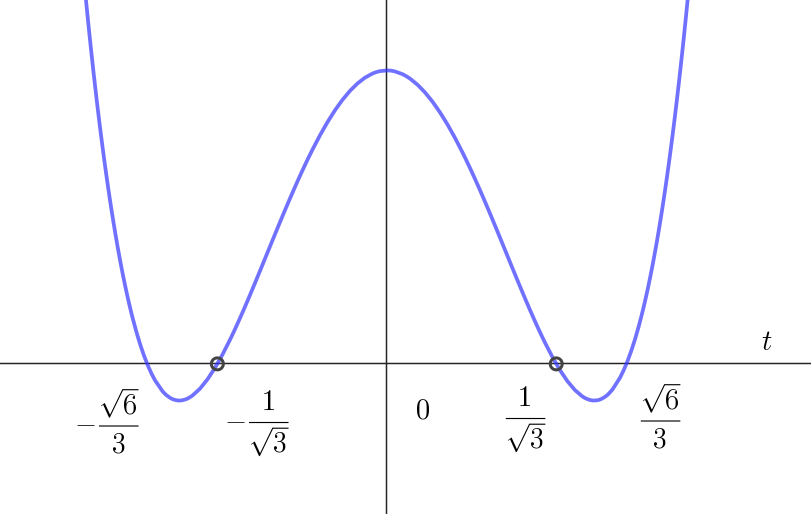
$t \leqq -\cfrac{\sqrt{6}}{3}, \quad -\cfrac{1}{\sqrt{3}} < t < \cfrac{1}{\sqrt{3}}, \quad t \geqq \cfrac{\sqrt{6}}{3}$


ページの先頭へ↑




メインメニュー　に戻る