筑波大学(理系) 2024年　問題2


$以下の問いに答えよ。$
$(1)\ \ x > 1,\ \ y > 1 \ \ のとき、不等式 \ \ \log _x y +\log _y x \geqq 2 \ \ が成り立つことを示せ。$
$(2)\ \ 座標平面において、連立不等式 \quad x >1 ,\ \ y > x ,\ \ \log _x y +\log _y x < \dfrac{5}{2} \ \ の表す領域を図示せよ。$
$(3)\ \ (2)の領域の中で \ \ x^2+y^2 < 12 \ \ を満たす部分に境界線を含めた図形を \ D\ とする。D\ の面積を求めよ。$


(1)


$x > 1,\ \ y > 1 \ \ だから\ \ \log x > 0, \ \ \log y > 0 \quad (底は正で、1\ でなければ何でもよい)$

$相加・相乗平均の不等式より$

$\log _x y +\log _y x =\cfrac{\log y}{\log x} + \cfrac{\log x}{\log y} \geqq 2\sqrt{\cfrac{\log y}{\log x} \times \cfrac{\log x}{\log y}}=2$

$ただし等号は \quad \cfrac{\log y}{\log x} = \cfrac{\log x}{\log y} \quad のときで \quad (\log x)^2=(\log y)^2 $

$\quad \log x > 0, \ \ \log y > 0 \quad だから \quad \log x =\log y \quad より \quad x=y \quad のとき$


(2)


$\log _x y +\log _y x < \dfrac{5}{2} \quad より \quad \cfrac{\log y}{\log x} + \cfrac{\log x}{\log y} < \cfrac{5}{2}$

$ y > x > 1 \ \ だから \quad \log x > 0, \ \ \log y > 0 $

$分母を払って$

　

$2(\log y )^2+ 2(\log x )^2 - 5(\log x)(\log y)< 0$

$(2\log y -\log x )(\log y -2\log x) < 0$

$2\log y -\log x < 0 , \quad \log y -2\log x > 0 \quad を満たすとすると$

$2\log x < \log y < \cfrac{1}{2}\log x $

$これより \quad \log x < 0 \quad となって不合理$

$よって \quad 2\log y -\log x >0 , \quad \log y -2\log x < 0 \quad を満たす$

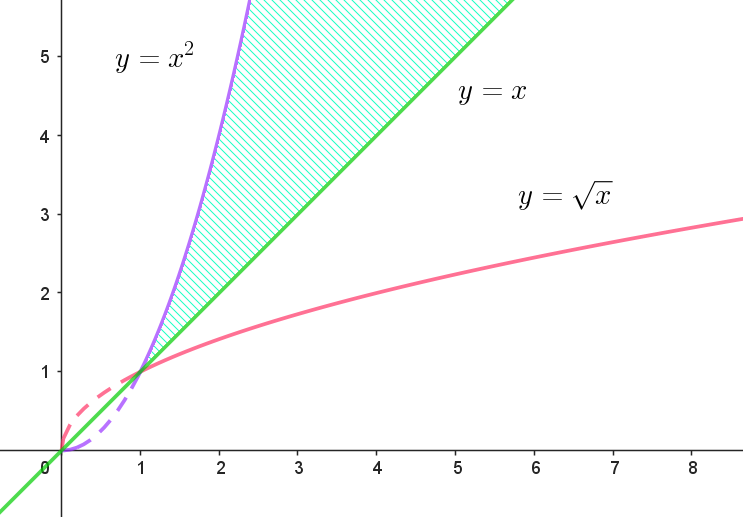
$y^2 > x , \quad y < x^2$

$x > 1,\quad y > x \quad を含めて求める領域は右図のとおり、ただし境界は含まず。$


(3)


$y=x^2 \ \ と円 \ \ x^2+y^2=12 \quad の交点 \ D\ は$

$y+y^2=12 \qquad y^2+y-12=0 \qquad (y-3)(y+4)=0$

$y > 1 \quad だから \quad y=3 \quad このとき \quad x > 1 \quad より \quad x=\sqrt{3} \quad よって \quad D(\sqrt{3},\ 3)$

$直線\ OD \ は \quad y=\sqrt{3}x $

$A(1,\ 1),\ \ B(1,\ \sqrt{3}) \ \ とすると点 \ B\ は \ \ y=\sqrt{3}x \ \ 上の点である。$

$y=x \ \ と円 \ x^2+y^2=12 \ \ の交点を \ C\ とする。$

　

$求める図形Dの面積を \ S\ とし、右図のように \ S_1,\ \ S_2\ をとる。$

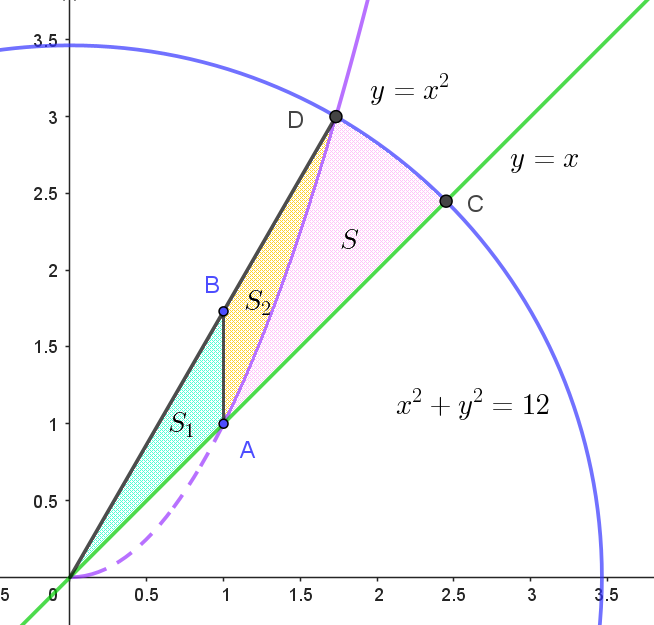
$直線 \ OC\ は \ \ y=x \ \ だから \ x\ 軸となす角は \ \ \dfrac{\pi}{4}$

$直線 \ OD\ は \ \ y=\sqrt{3}x \ \ だから \ x\ 軸となす角は \ \ \dfrac{\pi}{3}$

$したがって \quad \angle COD=\dfrac{\pi}{3}-\dfrac{\pi}{4}=\dfrac{\pi}{12}$

$扇形OCD=\pi \times 12 \times \cfrac{1}{24}=\cfrac{\pi}{2}$

$S_1=\triangle OAB=\cfrac{1}{2} \times 1 \times (\sqrt{3}-1)=\cfrac{\sqrt{3}-1}{2}$

\[S_2=\int_1^{\sqrt{3}}(\sqrt{3}x-x^2)dx=\big[\dfrac{\sqrt{3}}{2}x^2-\dfrac{1}{3}x^3\big]_1^{\sqrt{3}} =\dfrac{\sqrt{3}}{2} \times 3 -\dfrac{1}{3} \times 3\sqrt{3} -\big(\dfrac{\sqrt{3}}{2}-\dfrac{1}{3}\big)=\cfrac{1}{3}\]
$S=扇形OCD -S_1-S_2= \cfrac{\pi}{2}-\cfrac{\sqrt{3}-1}{2}-\cfrac{1}{3}=\cfrac{\pi}{2}-\cfrac{\sqrt{3}}{2}+\cfrac{1}{6}$


ページの先頭へ↑




メインメニュー　に戻る