筑波大学(理系) 2024年　問題1


$\triangle OAB において、OA=OB=4,\ \ AB=2\ \ とする。\angle OAB \ の二等分線と線分 \ OB\ の交点を \ C\ とし、$
$点 \ O\ から直線 \ AC\ に垂線 \ OD\ を引く。\vec{OA}=\vec{a},\ \ \vec{OB}=\vec{b}\ \ とおく。以下の問いに答えよ。$
$(1)\ \ \vec{AC}\ \ を \ \vec{a}\ と \ \vec{b}\ を用いて表せ。$
$(2)\ \ \vec{OD}\ \ を \ \vec{a}\ と \ \vec{b}\ を用いて表せ。$
$(3)\ \ \triangle BCD \ の面積を求めよ。$


(1)

　

$線分\ AC\ は \ \angle OAB\ の二等分線だから$

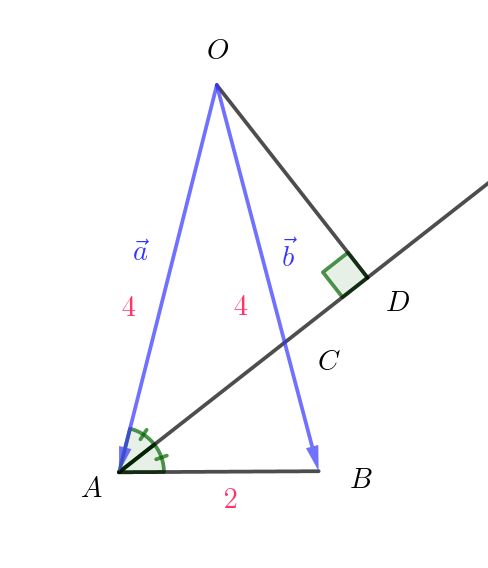
$OC:CB=AO:AB=4:2=2:1$

$\vec{AC}=\vec{AO}+\vec{OC}=-\vec{OA}+\dfrac{2}{3}\vec{OB}=-\vec{a}+\dfrac{2}{3}\vec{b}$


(2)


$\triangle OAB \ に余弦定理を用いて$
\begin{eqnarray*} \vec{a}\cdot \vec{b} &=&|\vec{OA}||\vec{OB}|\cos \angle AOB\\ \\ &=&|\vec{OA}||\vec{OB}| \times \cfrac{OA^2+OB^2-AB^2}{2OA \cdot OB}\\ \\ &=&\cfrac{1}{2}(OA^2+OB^2-AB^2)\\ \\ &=&\cfrac{1}{2}(4^2+4^2-2^2)\\ \\ &=&14 \end{eqnarray*}
$点D\ は直線 \ AC\ 上の点だから \ k\ を実数として$

$\vec{AD}=k\vec{AC}=k(-\vec{a}+\dfrac{2}{3}\vec{b})=-k\vec{a}+\dfrac{2}{3}k\vec{b}$

$\vec{OD}=\vec{OA}+\vec{AD}=\vec{a}+(-k\vec{a}+\dfrac{2}{3}k\vec{b})=(1-k)\vec{a}+\dfrac{2}{3}k\vec{b}$

$OD \perp AC \quad より$

$\vec{OD} \cdot \vec{AC}=0$

$\big((1-k)\vec{a}+\dfrac{2}{3}k\vec{b}\big) \cdot \big(-\vec{a}+\dfrac{2}{3}\vec{b}\big)=0$

$\big(3(1-k)\vec{a}+2k\vec{b}\big) \cdot \big(-3\vec{a}+2\vec{b}\big)=0$

$-9(1-k)|\vec{a}|^2+ 6(1-k)\vec{a} \cdot \vec{b} -6k\vec{a} \cdot \vec{b} + 4k|\vec{b}|^2=0$

$-9 \times 4^2(1-k)+6 \times 14 (1-k) - 6 \times 14 k + 4 \times 4^2k=0$

$\therefore \ \ k=\cfrac{3}{2}$

$\vec{AD}=\cfrac{3}{2}\vec{AC}=\cfrac{3}{2}(-\vec{a}+\dfrac{2}{3}\vec{b})=-\cfrac{3}{2}\vec{a}+\vec{b}$

$よって$

\begin{eqnarray*} \vec{OD} &=&\vec{OA} + \vec{AD} \\ \\ &=& \vec{a} -\cfrac{3}{2}\vec{a}+\vec{b}\\ \\ &=& -\cfrac{1}{2}\vec{a} +\vec{b} \end{eqnarray*}

(3)

　

$(1)より \quad \vec{AC}=-\vec{a} + \cfrac{2}{3}\vec{b} \quad だから$

$|\vec{AC}|^2=|\vec{a}|^2+\cfrac{4}{9}|\vec{b}|^2- \cfrac{4}{3}\vec{a} \cdot \vec{b}=4^2 +\cfrac{4}{9} \times 4^2-\cfrac{4}{3} \times 14=\cfrac{40}{9}$

$\therefore \ \ |\vec{AC}|=\cfrac{2\sqrt{10}}{3}$

$(2)より \quad \vec{OD}=-\cfrac{1}{2}\vec{a} +\vec{b} \quad だから $

$|\vec{OD}|^2=\cfrac{1}{4}|\vec{a}|^2+|\vec{b}|^2- \vec{a} \cdot \vec{b}=\cfrac{1}{4} \times 4^2+4^2-14=6$

$\therefore \ \ |\vec{OD}|=\sqrt{6}$

$よって、\triangle OAC=\cfrac{1}{2} \times AC \times OD=\cfrac{1}{2} \times \cfrac{2\sqrt{10}}{3} \times \sqrt{6}=\cfrac{2\sqrt{15}}{3}$

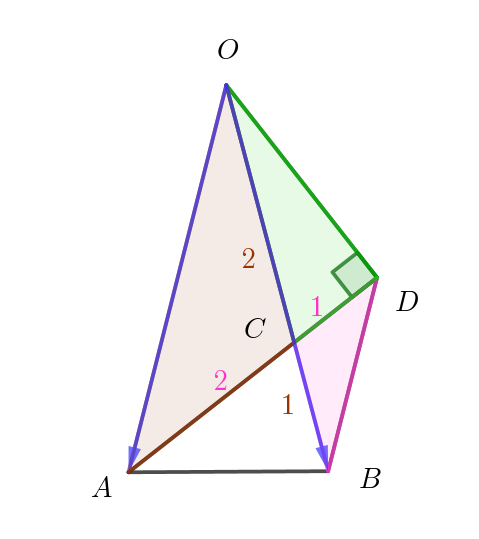
$高さが等しい \ 2\ つの三角形の面積比は底辺の比に等しいから$

$\triangle OCD=\triangle OAC \times \cfrac{1}{2}=\cfrac{2\sqrt{15}}{3} \times \cfrac{1}{2}=\cfrac{\sqrt{15}}{3}$

$\therefore \ \ \triangle BCD=\triangle OCD \times \cfrac{1}{2}=\cfrac{\sqrt{15}}{3} \times \cfrac{1}{2}=\cfrac{\sqrt{15}}{6}$


$(参考)$

$\triangle BCD \ と \ \triangle OCA \ は \ 2\ 辺の比とその間の角が等しいので \quad \triangle BCD \sim \triangle OCA$

$相似比は \ \ 1 : 2 \ \ だから 面積比は \ \ 1:4$

$\triangle BCD=\triangle OCA \times \cfrac{1}{4}=\cfrac{2\sqrt{15}}{3} \times \cfrac{1}{4}=\cfrac{\sqrt{15}}{6}$


ページの先頭へ↑




メインメニュー　に戻る