筑波大学(理系) 2018年 問題5
\[f(x)=\int _0^x \cfrac{4\pi}{t^2+\pi ^2}dt \ \ とし、c \geqq \pi \ \ とする。数列 \ \ \{a_n\}\ \ を \ \ a_1=c,\ \ a_{n+1}=f(a_n)\ \ (n=1,2,\cdots)\ \ で定める。\]
$\qquad (1)\ \ f(\pi)\ を求めよ。また、x \geqq \pi \ \ のとき、0 < f'(x) \leqq \cfrac{2}{\pi} \ \ が成り立つことを示せ。$
$\qquad (2)\ \ すべての自然数 \ n\ に対して、a_n \geqq \pi \ \ が成り立つことを示せ。$
$\qquad (3)\ \ すべての自然数 \ n\ に対して、|a_{n+1}-\pi| \leqq \cfrac{2}{\pi}|a_n -\pi|\ \ が成り立つことを示せ。$
\[\quad また、\lim_{n \rightarrow \infty} a_n \ \ を求めよ。\]
$(解説)$
$(1)\ \ この形の分数式の置換積分は必須事項です。f'(x)の不等式はさほど見つけにくいものではありません。$
$(2)\ \ (1)でf'(x)>0 \ \ がいえているので、f(x)\ は単調増加です。数学的帰納法をつかうのがいいでしょう。$
$(3)\ \ (1)でf(\pi)=\pi \ \ を求めているので、平均値の定理がつかえることがわかります。$
$なお、研究として \ f(x)\ を定積分でなく普通の関数の表現で表し、極限値をグラフから考えてみます。$
(1)
\[f(\pi)=\int _0^{\pi} \cfrac{4\pi}{t^2+\pi ^2}dt \quad において \quad t=\pi \tan \theta \quad とおくと\] \[\qquad dt=\pi \cfrac{d\theta}{\cos ^2 \theta} \qquad \quad \begin{array}{c|c} t & \ 0 \rightarrow \pi \quad \\ \hline \theta & \ 0 \rightarrow \cfrac{\pi}{4}\\ \end{array} \] \[f(\pi)=4\pi \int _0^{\small{\cfrac{\pi}{4}}} \cfrac{\pi \dfrac{d\theta}{\cos ^2\theta}}{\pi ^2(\tan ^2 \theta +1)}=4\int _0^{\small{\cfrac{\pi}{4} } }d\theta=\pi\]
$また \qquad f'(x)=\cfrac{4\pi}{x^2+\pi ^2} \quad で $
$\quad x \geqq \pi \quad より \quad x^2 +\pi ^2 \geqq \pi ^2 + \pi ^2 =2\pi ^2 \qquad \therefore \ \ \cfrac{1}{x^2 + \pi ^2} \leqq \cfrac{1}{2\pi ^2} $
$\quad f'(x) \leqq 4\pi \times \cfrac{1}{2\pi ^2} =\cfrac{2}{\pi}$
$明らかに f'(x) > 0 \quad だから \quad 0 < f'(x) \leqq \cfrac{2}{\pi}$
(2)
$数学的帰納法で示す。$
(i)$\ \ a_1=c \geqq \pi \quad だから \quad n = 1\ \ のとき成りたつ。$
(ii)$\ \ n=k \ \ のとき成りたつとすると \qquad a_k \geqq \pi$
$\quad f'(x) > 0 \quad より \quad f(x) \ は単調増加関数だから \qquad f(a_k) \geqq f(\pi) $
$\qquad \therefore \ \ a_{k+1} =f(a_k) \geqq \pi$
$よって \quad n=k+1 \ \ のときも成りたつ$
(i),(ii)$よりすべての自然数 \ n\ について \qquad a_n \geqq \pi$
(3)
$f(x) は連続で微分可能だから平均値の定理より$
$\qquad \cfrac{f(a_n)-f(\pi)}{a_n-\pi}=f'(c) \quad となる \ c\ が区間 \ (\pi,\ a_n)\ に存在する。$
$(2)より \quad 0 < f'(c) \leqq \cfrac{2}{\pi} \quad だから$
$\qquad |\cfrac{f(a_n)-f(\pi)}{a_n-\pi}| =|f'(c)| \leqq \cfrac{2}{\pi} $
$\qquad |f(a_n)-f(\pi)| \leqq \cfrac{2}{\pi}|a_n-\pi| $
$(1)より \quad f(\pi)=\pi \quad だから$
$\qquad |a_{n+1}-\pi| \leqq \cfrac{2}{\pi}|a_n-\pi| $
$この不等式を繰り返しつかって$
\begin{eqnarray*} |a_n-\pi| & \leqq & \cfrac{2}{\pi}|a_{n-1}-\pi|\\ & \leqq & \big(\cfrac{2}{\pi}\big)^2 |a_{n-2}-\pi|\\ & & \vdots\\ & \leqq & \big(\cfrac{2}{\pi}\big)^{n-1} |a_1-\pi|\\ \end{eqnarray*} $ここで \quad 0 < \cfrac{2}{\pi} < 1 \quad だから \quad n \longrightarrow \infty \quad のとき \quad \big(\cfrac{2}{\pi}\big)^{n-1} \longrightarrow 0$
$\quad 0 < |a_n-\pi| \quad だから はさみうちの原理により \qquad a_n-\pi \longrightarrow 0 $
\[したがって \qquad \lim _{n \rightarrow \infty} a_n =\pi\]
$(研究)$
$定積分で表された関数 \ f(x)\ を具体的に表現して、この極限値の意味を考えてみましょう。$
\[f(x)=\int _0^x \cfrac{4\pi}{t^2+\pi ^2}dt \quad において \quad t=\pi \tan \theta \quad と変換すると\] \[\qquad dt=\cfrac{\pi}{\cos ^2 \theta}d\theta \qquad \begin{array}{c|c} t & \ 0 \rightarrow x \quad \\ \hline \theta &\ 0 \rightarrow \alpha\\ \end{array} \] $ただし \quad \tan \alpha =\cfrac{x}{\pi} \quad すなわち \quad \alpha =\tan ^{-1}\big(\cfrac{x}{\pi}\big)$
\[f(x)=\int _0^{\alpha} \cfrac{4}{1+\tan ^2\theta}\cdot \cfrac{d\theta}{\cos ^2 \theta} =\int _0^{\alpha} 4 d\theta =4\alpha =4\tan ^{-1}\big(\cfrac{x}{\pi}\big)\]
$逆三角関数が出てしまいましたが、これが関数 \ f(x)\ の正体です。$
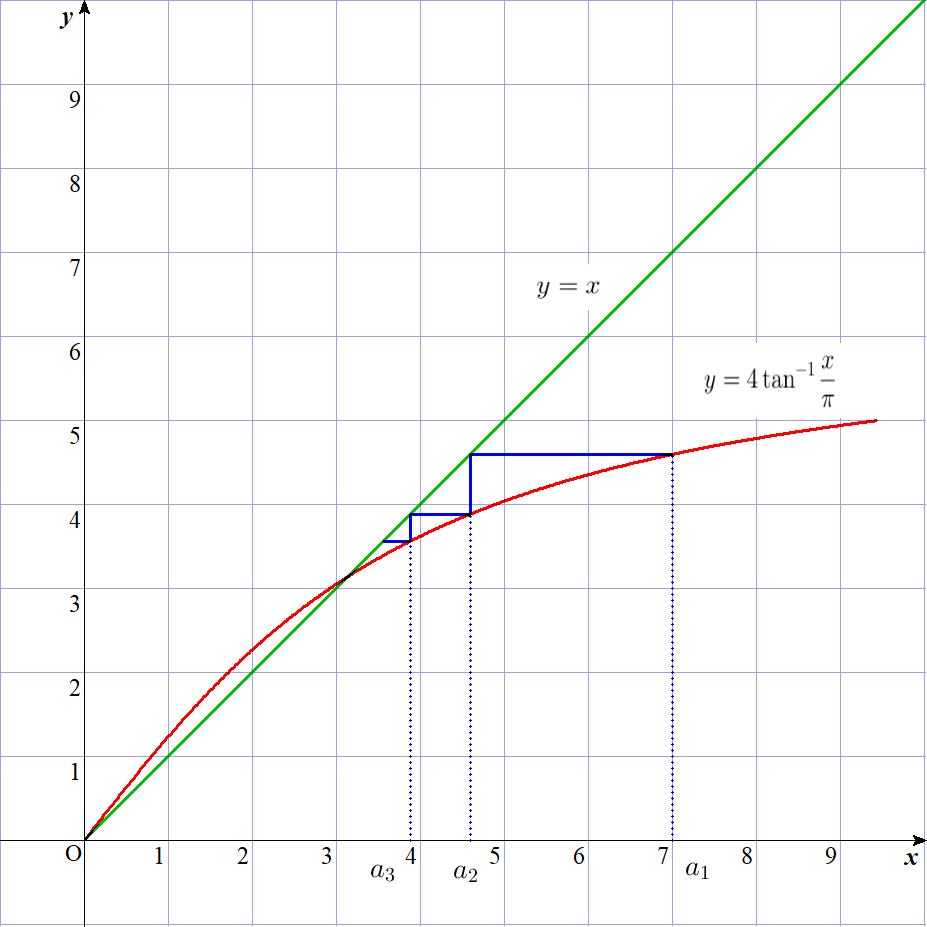
$\tan x \ のグラフが単調増加であり、その逆関数のグラフは$
$直線 \ y=x\ に関して対称であることを考えると$
$y=f(x)\ のグラフは単調増加であることがわかります。$
$(逆関数については($逆関数$)を参考にしてください。)$
$また、f(\pi)=4\tan ^{-1}\big(\cfrac{\pi}{\pi}\big)=4\tan ^{-1}1=4 \times \cfrac{\pi}{4}=\pi$
$であるから \ \ y=f(x) \ と \ y=x \ の交点の座標は\ (\pi,\ \pi)\ である$
$こともわかります。$
$これらのことから、a_1=c \ \ (c \geqq \pi)\ から順次 \ \ a_2,\ a_3,\cdots $
$を求めると、右のグラフのようになります。$
$なお、グラフでは \ c=7\ としました。$
$a_n \ は交点の \ x\ 座標 \ \pi \ に限りなく近づくことがわかります。$
メインメニュー に戻る