MY MATH NOTE

筑波大学(理系) 2018年　問題1

$0 < \theta < \cfrac{\pi}{2}\ \ とする。放物線 \ y=x^2 \ 上に \ 3点\ \ O(0,\ 0),\ \ A(\tan \theta,\ \tan ^2 \theta),\ \ B((-\tan \theta,\ \tan ^2 \theta)\ \ をとる。$
$三角形OABの内心の \ y\ 座標を \ p\ とし、外心の \ y\ 座標を \ q\ とする。また、正の実数 \ a\ に対して、$
$直線 \ \ y=a\ \ と放物線 \ \ y=x^2\ \ で囲まれた図形の面積を \ S(a)\ で表す。$
$(1)\ \ p,\ q\ を \ \cos \theta \ \ を用いて表せ。$
$(2)\ \ \cfrac{S(p)}{S(q)}\ \ が整数であるような \ \ \cos \theta \ \ の値をすべて求めよ。$

(1)

　
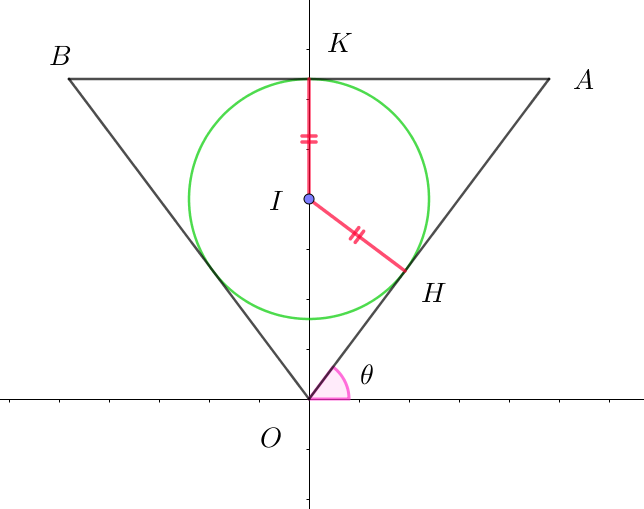
(i)$\ \ 内心Iについて$

$直線OAの傾き=\cfrac{\tan ^2 \theta}{\tan \theta}=\tan \theta$

$したがって　直線OAとx軸の正方向となす角が\theta である。$

$内心Iから線分OAに下ろした垂線の足をHとすると \quad \angle HOI=\cfrac{\pi}{2}-\theta$
$よって \quad IH=p\sin (\cfrac{\pi}{2}-\theta)=p\cos \theta$

$また　Iから線分ABに下ろした垂線の足をKとすると　IK=\tan ^2\theta -p$

$IH=IK \ \ より \quad p\cos \theta =\tan ^2 \theta -p \hspace{3em} p(1+\cos \theta)=\tan ^2 \theta$

$\therefore \ \ p=\cfrac{\tan ^2 \theta}{1+\cos \theta }=\cfrac{\dfrac{1}{\cos ^2 \theta}-1}{1+\cos \theta }=\cfrac{1-\cos ^2 \theta}{(1+\cos \theta)\cos ^2\theta} =\cfrac{1-\cos \theta}{\cos ^2\theta}$

　
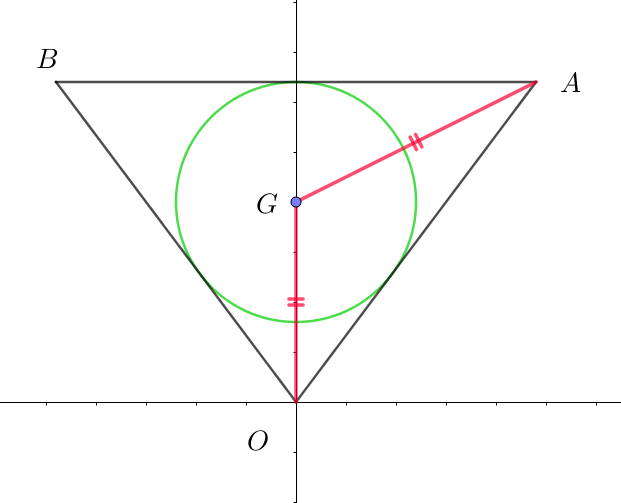
(ii)$\ \ 外心Gについて$

$外心をG(0,q)とすると　GO=GA \quad より \quad q^2=\tan ^2 \theta +(tan ^2 \theta - q)^2$

$q^2=\tan ^2 \theta +tan ^4 \theta - 2q\tan ^2 \theta +q^2 \hspace{3em} 2q\tan ^2 \theta = \tan ^2 \theta +tan ^4 \theta $

$明らかに \quad \tan \theta \ne 0 \quad だから \qquad q=\cfrac{1}{2}(1+\tan ^2 \theta)=\cfrac{1}{2\cos ^2 \theta}$

(2)

　
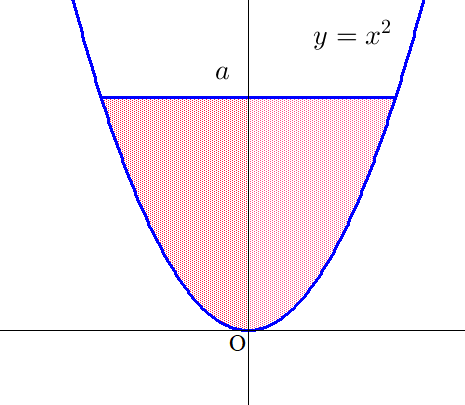
\[S(a)=2\int _0^axdy=2\int _0^a\sqrt{y}dy=\cfrac{4}{3}\big[y^{\small{\cfrac{3}{2}}}\big] _0^a=\cfrac{4}{3}a\sqrt{a}\] $また(2)より$

$\quad \cfrac{p}{q}=\cfrac{1-\cos \theta}{\cos ^2\theta} \times 2\cos ^2 \theta =2(1-\cos \theta ) =2\{1-(1-2\sin ^2 \cfrac{\theta}{2})\}=4\sin ^2 \cfrac{\theta}{2}$

$したがって$

$\qquad \cfrac{S(p)}{S(q)}=\cfrac{4p\sqrt{p}}{3} \times \cfrac{3}{4q\sqrt{q}}=\big(\cfrac{p}{q}\big)^{\small{\cfrac{3}{2}}} =\big(4\sin ^2 \small{\cfrac{\theta}{2}}\big)^{\small{\cfrac{3}{2}}}=\normalsize{8\sin ^3 \cfrac{\theta}{2}} $

$これが整数となるのは \quad \sin ^3 \cfrac{\theta}{2}=1,\quad \cfrac{1}{2},\quad \cfrac{1}{4},\quad \cfrac{1}{8} \quad のときであるから$

$\qquad \sin \cfrac{\theta}{2}=1,\quad \cfrac{1}{\sqrt[3]{2}},\quad \cfrac{1}{\sqrt[3]{4}},\quad \cfrac{1}{2}$

$0 < \theta < \cfrac{\pi}{2} \quad だから \quad 0 < \cos \theta < 1 \hspace{3em} \cos \theta =1-2\sin ^2\cfrac{\theta}{2} \quad に代入して$

(i)$\ \ \sin \cfrac{\theta}{2}=1 \quad のとき　\quad \cos \theta =-1 \quad となり不適$

(ii)$\ \ \sin \cfrac{\theta}{2}= \cfrac{1}{\sqrt[3]{2}} \quad のとき \quad \cos \theta =1-\cfrac{2}{\sqrt[3]{4}}=1-\cfrac{\sqrt[3]{8}}{\sqrt[3]{4}}=1-\sqrt[3]{2} \qquad これは負だから不適$

(iii)$\ \ \sin \cfrac{\theta}{2}= \cfrac{1}{\sqrt[3]{4}} \quad のとき \quad \cos \theta =1-\cfrac{2}{\sqrt[3]{16}}=1-\cfrac{\sqrt[3]{8}}{\sqrt[3]{16}}=1-\cfrac{1}{\sqrt[3]{2}}=1-\cfrac{\sqrt[3]{4}}{2}$

(iv)$\ \ \sin \cfrac{\theta}{2}= \cfrac{1}{2} \quad のとき \quad \cos \theta =1-\cfrac{2}{4}=\cfrac{1}{2}$

(i)～(iv)$より \quad \cos \theta =1-\cfrac{\sqrt[3]{4}}{2},\quad \cfrac{1}{2}$

ページの先頭へ↑