東京都立大学(数理) 2025年　問題1


$a \ は \ a > 1 \ をみたす実数とする。座標平面において、連立不等式 \quad 0 \leqq x \leqq 1, \quad 0 \leqq y \leqq ax^2 \quad の表す領域の$
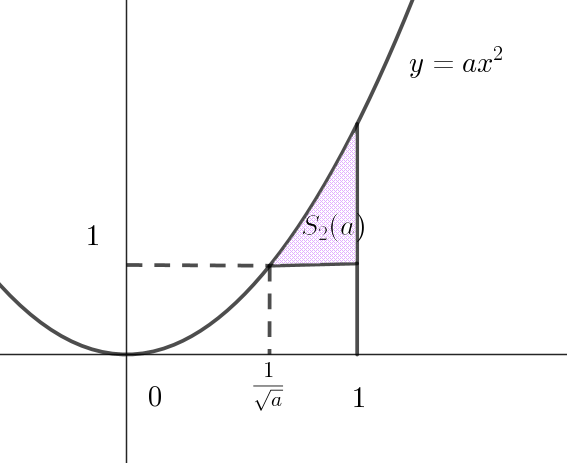
$面積を \ S_1(a) \ とし、連立不等式 \quad 0 \leqq x \leqq 1, \quad 1 \leqq y \leqq ax^2 \quad の表す領域の面積を \ S_2(a)\ とする。以下の問い$
$に答えなさい。$
$(1)\ \ S_1(a)\ \ を \ a\ を用いて表しなさい。$
$(2)\ \ S_2(a)\ \ を \ a\ を用いて表しなさい。$
$(3)\ \ a\ が \ \ a > 1\ \ の範囲を動くとき、S_1(a)-2S_2(a)\ \ の値が最大となる \ a\ の値を求めなさい。$


(1)

　

\begin{eqnarray*} S_1(a) &=&\int_0^1 ax^2dx\\ \\ &=&a\big[\dfrac{x^3}{3}\big]_0^1\\ \\ &=&\dfrac{a}{3} \end{eqnarray*}

(2)


$y=ax^2 \ \ と \ \ y=1\ \ の交点は \quad ax^2=1 \ \ より \quad x=\dfrac{1}{\sqrt{a}}$

　

\begin{eqnarray*} S_2(a) &=&\int_{\scriptsize{\dfrac{1}{\sqrt{a}}}}^1 (ax^2-1)dx\\ \\ &=&\big[\dfrac{a}{3}x^3-x\big]_{\scriptsize{\dfrac{1}{\sqrt{a}}}}^1 \\ \\ &=&\big(\dfrac{a}{3}-1\big)-\big(\dfrac{a}{3} \times \dfrac{1}{a\sqrt{a}} -\dfrac{1}{\sqrt{a}}\big)\\ \\ &=&\dfrac{a}{3}-1 -\dfrac{1}{3\sqrt{a}} +\dfrac{1}{\sqrt{a}}\\ \\ &=&\dfrac{a}{3} +\dfrac{2}{3\sqrt{a}} -1 \end{eqnarray*}

(3)


$S(a)=S_1(a)-2S_2(a) \quad とおくと$

\begin{eqnarray*} S(a) &=&\dfrac{a}{3}-2\big(\dfrac{a}{3} +\dfrac{2}{3\sqrt{a}} -1\big)\\ \\ &=&-\dfrac{a}{3} - \dfrac{4}{3\sqrt{a}} +2\\ \\ &=&-\dfrac{a}{3} - \dfrac{4}{3}a^{\scriptsize{-\dfrac{1}{2}}} +2\\ \end{eqnarray*}
$S'(a)=-\dfrac{1}{3}+\dfrac{2}{3}a^{\scriptsize{-\dfrac{3}{2}}}=\dfrac{1}{3}(2a^{\scriptsize{-\dfrac{3}{2}}}-1)$

$S'(a)=0 \quad より \quad a^{\scriptsize{-\dfrac{3}{2}}}=\dfrac{1}{2}$

$a=\big(\dfrac{1}{2}\big)^{\scriptsize{-\dfrac{2}{3}}}=2^{\scriptsize{\dfrac{2}{3}}}=\sqrt[3]{4}$

$増減表$
\[ \begin{array}{c||c|c|c|c|c} a & 1 & \cdots & \sqrt[3]{4} & \cdots \\ \hline S'(a) & & + & 0 & - \\ \hline S(a) & & \nearrow & 極大 & \searrow & \\ \end{array} \]
$a=\sqrt[3]{4}\ \ のとき \ \ S(a)\ は極大かつ最大となり最大値は$

\begin{eqnarray*} S(\sqrt[3]{4}) &=&-\dfrac{\sqrt[3]{4}}{3}-\dfrac{4}{3} \times \big(4^{\scriptsize{\dfrac{1}{3}}}\big)^{\scriptsize{-\dfrac{1}{2}}} +2\\ \\ &=&-\dfrac{\sqrt[3]{4}}{3}-\dfrac{4}{3} \times 4^{-\scriptsize{\dfrac{1}{6}}}+2\\ \\ &=&-\dfrac{\sqrt[3]{4}}{3}-\dfrac{4}{3} \times 2^{-\scriptsize{\dfrac{1}{3}}}+2\\ \\ &=&-\dfrac{\sqrt[3]{4}}{3}-\dfrac{4}{3} \times \dfrac{1}{\sqrt[3]{2}}+2\\ \\ &=&-\dfrac{\sqrt[3]{4}}{3}-\dfrac{4}{3} \times \dfrac{\sqrt[3]{4}}{2}+2\\ \\ &=&2-\sqrt[3]{4} \end{eqnarray*}

ページの先頭へ↑



メインメニュー　に戻る