東京都立大学(数理) 2024年 問題2
$R\ を正の実数とする。複素数平面上で、点 \ a\ を中心とする半径 \ R\ の円 \ C\ を考え、0 < |z-a| < R \ \ をみたす$
$点 \ z\ をとる。a\ と \ z\ を結ぶ直線を \ l\ とし、z\ を通り \ l\ に直交する直線と円 \ C\ の交点を \ p,\ q\ とする。さらに$
$点 \ p,\ q\ における \ C\ の接線と \ l\ の交点を \ w\ とする。以下の問いに答えなさい。$
$(1)\ \ 関係式 \ \ (w-a)(\overline{z} -\overline{a})=R^2 \ \ が成り立つことを示しなさい。$
$(2)\ \ a=0,\ \ R=1 \ \ とする。z\ が \ \ |z| < 1、\ \ Re \ z=\dfrac{1}{4}\ \ をみたしながら動くとき、点 \ w\ はどのような図形を$
$\quad 描くか求め、図示しなさい。ただし、Re \ z \ は \ z\ の実部を表す。$
(1)
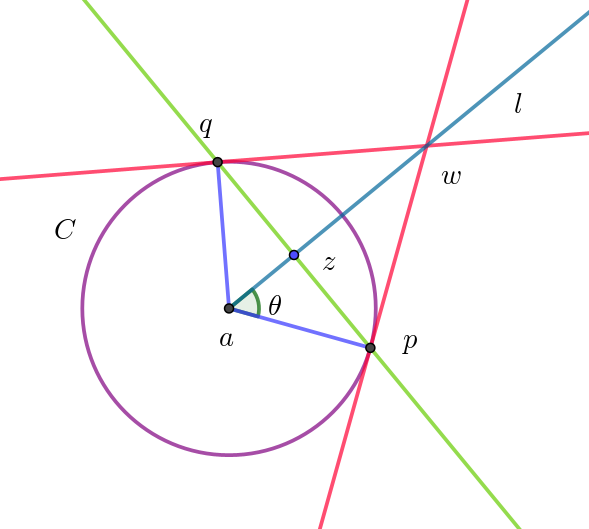
$それぞれの斜辺は円 \ C\ の半径だから \ \ ap=aq,\quad az\ は共通$
$ゆえに \quad \triangle apz \equiv \triangle aqz$
$\therefore \ \ \angle paz =\angle qaz$
$円の接線は、接点と円の中心を結ぶ線分に垂直であるから$
$\angle apw=\angle aqw=90°$
$直角三角形 \ apw \ と直角三角形 \ aqw \ において $
$それぞれの斜辺は共通、\quad ap=aq \ \ (半径)$
$ゆえに \quad \triangle apw \equiv \triangle aqw$
$\therefore \ \ \angle paw =\angle qaw$
$したがって、3\ 点 \ a,\ z,\ w\ は一直線上にあるから$
$z-a=k(w-a) \ \ (k\ は実数)\ \ とおける。$
$また \quad \angle paz =\theta \ \ とおくと$
$|z-a|=R\cos \theta,\quad |w-a|=\cfrac{R}{\cos \theta}$
$よって \quad k=\cfrac{|z-a|}{|w-a|}=R\cos \theta \times \cfrac{\cos \theta}{R}=\cos ^2 \theta $
$このとき$
\begin{eqnarray*} & &(w-a)(\overline{z}-\overline{a})\\ \\ &=&(w-a)(\overline{z-a})\\ \\ &=&(w-a)(\overline{k(w-a)})\\ \\ &=&k|w-a|^2\\ \\ &=&\cos ^2 \theta \times \big(\cfrac{R}{\cos \theta}\big)^2\\ \\ &=&R^2 \end{eqnarray*}
(2)
$Re \ z=\cfrac{1}{4} \ \ より \ \ z=\cfrac{1}{4}+ti \ \ (t\ は実数)\ \ とおける。$
$ただし \quad |z|<1 \ \ より \quad \cfrac{1}{16}+t^2<1 $
$(1)より \quad (w-a)(\overline{z}-\overline{a})=R^2 \quad において$
$a=0,\ \ R=1\ \ だから \quad w \overline{z} =1$
$w=\cfrac{1}{\overline{z}}=\cfrac{1}{\cfrac{1}{4}-ti}=\cfrac{\cfrac{1}{4}+ti}{\cfrac{1}{16}+t^2}$
$x^2+y^2=\cfrac{\cfrac{1}{16}+t^2}{\big(\cfrac{1}{16}+t^2\big)^2}=\cfrac{1}{\cfrac{1}{16}+t^2}=4x$
$\therefore \ \ (x-2)^2+y^2=4$
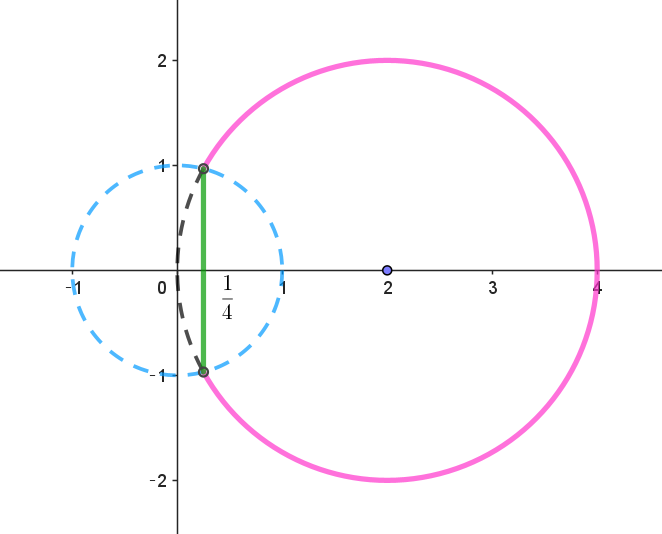
$点 \ w\ は中心(2,\ 0),\ \ 半径 \ 2\ の円を描く。$
$ただし \ \ \cfrac{1}{16}+t^2 < 1\ \ だから \quad \cfrac{1}{16}+t^2=\cfrac{\dfrac{1}{4}}{x} < 1 \qquad x > 0 \ \ より \quad x > \cfrac{1}{4}$
$グラフは右図のとおり$
メインメニュー に戻る