東京都立大学(理系) 2025年 問題3
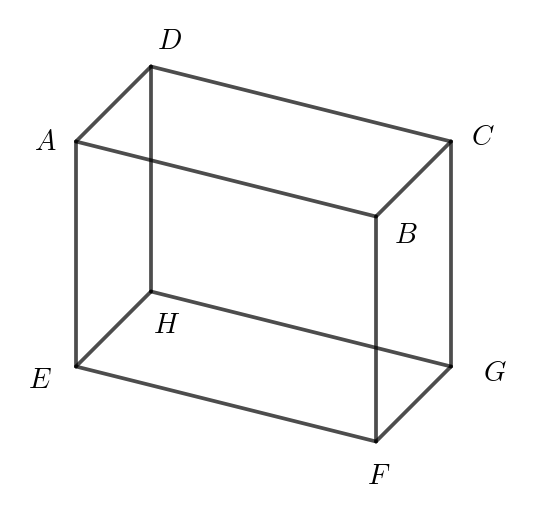
$下の図の直方体 \ ABCD-EFGH \ において、AB=3,\ \ AD=1,\ \ AE=2 \ \ とする。t\ は \ \ 0 < t < 1\ \ をみたす$
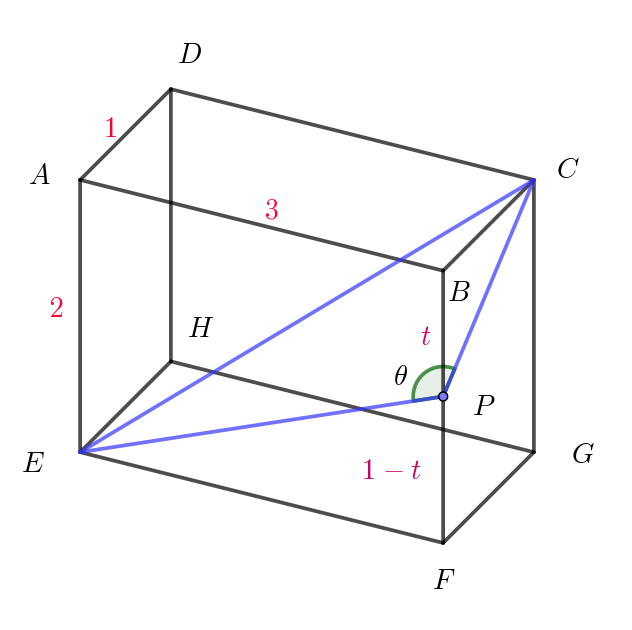
$実数とする。線分BF \ を \ t:(1-t) \ \ に内分する点をP\ とする。以下の問いに答えなさい。$
$(1)\ \ \theta=\angle CPE \ \ とおく。\cos \theta \ \ を \ t\ を用いて表しなさい。$
$(2)\ \ \triangle CEP\ \ の面積を \ S(t)\ とする。S(t)\ を \ t\ を用いて表しなさい。$
$(3)\ \ t\ が \ \ 0 < t < 1 \ \ の範囲を動くとき、(2)の \ S(t)\ の最小値を求めなさい。また、そのときの \ t\ の値を求めな$
$\quad さい。$
$\hspace{5em}$
(1)
$CE^2=AB^2+AD^2+AE^2=3^2+1^2+2^2=14$
$\ \ 直角三角形 BCP \ \ において \ \ BP=2t, \ \ BC=1 \ \ だから$
$CP^2=BP^2+BC^2=4t^2+1$
$\ \ 直角三角形 EFP \ \ において \ \ EF=3, \ \ FP=2(1-t) \ \ だから$
$EP^2=EF^2+FP^2=3^2+4(1-t)^2=4t^2-8t+13$
$\triangle CEP \ \ に余弦定理を用いて$
\begin{eqnarray*} \cos \theta &=&\dfrac{CP^2+EP^2-CE^2}{2CP \cdot EP}\\ \\ &=&\cfrac{(4t^2+1)+(4t^2-8t+13)-14}{2\sqrt{4t^2+1}\sqrt{4t^2-8t+13}}\\ \\ &=&\cfrac{8t^2 -8t}{2\sqrt{4t^2+1}\sqrt{4t^2-8t+13}}\\ \\ &=&\cfrac{4t(t-1)}{\sqrt{4t^2+1}\sqrt{4t^2-8t+13}}\\ \end{eqnarray*}
$(ベクトルの内積を用いた解法)$
$\vec{AB}=\vec{a},\ \ \vec{AD}=\vec{b},\ \ \vec{AE}=\vec{c} \ \ とおくと \quad \vec{a}\cdot \vec{b}=\vec{b}\cdot \vec{c}=\vec{c}\cdot \vec{a}=0$
$\vec{AP}=(1-t)\vec{AB}+t\vec{AF}=(1-t)\vec{a}+t(\vec{a}+\vec{c})=\vec{a}+t\vec{c}$
$\vec{PC}=\vec{AC}-\vec{AP}=(\vec{a}+\vec{b})-(\vec{a}+t\vec{c})=\vec{b}-t\vec{c} \ \ より$
$|\vec{PC}|^2=|\vec{b}-t\vec{c}|^2=|\vec{b}|^2+t^2|\vec{c}|^2-2t\vec{b}\cdot \vec{c}=1+4t^2$
$\vec{PE}=\vec{AE}-\vec{AP}=\vec{c}-(\vec{a}+t\vec{c})=-\vec{a}+(1-t)\vec{c} \ \ より$
$|\vec{PE}|^2=|-\vec{a}+(1-t)\vec{c}|^2=|\vec{a}|^2+(1-t)^2|\vec{c}|^2-2(1-t)\vec{a}\cdot \vec{c}=9+4(1-t)^2=4t^2-8t+13$
$\vec{PC}\cdot \vec{PE}=(\vec{b}-t\vec{c}) \cdot (-\vec{a}+(1-t)\vec{c})=-t(1-t)|\vec{c}|^2=-4t(1-t)$
$\cos \theta=\dfrac{\vec{PC} \cdot \vec{PE}}{|\vec{PC}||\vec{PE}|}=\dfrac{-4t(1-t)}{\sqrt{4t^2+1}\sqrt{4t^2-8t+13}}$
(2)
\begin{eqnarray*} S(t) &=&\dfrac{1}{2} \times CP \times EP \times \sin \theta\\ \\ &=&\dfrac{1}{2} \times CP \times EP \times \sqrt{1-\cos ^2 \theta}\\ \\ &=&\dfrac{1}{2} \times \sqrt{4t^2+1} \times \sqrt{4t^2-8t+13} \times \sqrt{1-\cfrac{16t^2(t-1)^2}{(4t^2+1)(4t^2-8t+13)}}\\ \\ &=&\dfrac{1}{2} \sqrt{(4t^2+1)(4t^2-8t+13)- 16t^2(t-1)^2)}\\ \\ &=&\dfrac{1}{2} \sqrt{40t^2-8t+13}\\ \end{eqnarray*}
(3)
$T(t)=40t^2-8t+13 \quad とおくと$
$T(t)=40(t^2-\dfrac{1}{5}t)+13=40(t-\dfrac{1}{10})^2+13-\dfrac{2}{5}=40(t-\dfrac{1}{10})^2+\dfrac{63}{5}$
$0 < t < 1 \ \ の範囲で \quad T(t)\ は \ \ t=\dfrac{1}{10} \ \ のとき \ \ 最小値 \ \ \dfrac{63}{5}\ \ をもつから$
$S(t)\ の最小値は \ t=\dfrac{1}{10}\ \ のとき \ \ \dfrac{1}{2} \times \sqrt{\dfrac{63}{5}}=\dfrac{3\sqrt{35}}{10}$
メインメニュー に戻る