東京大学(理系) 2025年　問題6


$複素数平面上の点 \ \dfrac{1}{2}\ を中心とする半径 \ \dfrac{1}{2}\ の円の周から原点を除いた曲線を \ C\ とする。$
$(1)\ \ 曲線 \ C\ 上の複素数 \ z\ に対し、\dfrac{1}{z}\ の実部は \ 1\ であることを示せ。$
$(2)\ \ \alpha , \ \beta \ を曲線 \ C\ 上の相異なる複素数とするとき、\dfrac{1}{\alpha^2}+\dfrac{1}{\beta^2}\ \ がとりうる範囲を複素数平面上に図示せよ。$
$(3)\ \ \gamma \ を(2)で求めた範囲に属さない複素数とするとき、\dfrac{1}{\gamma} \ \ の実部がとりうる値の最大値と最小値を求めよ。$


(1)


$点 \ \dfrac{1}{2}\ を中心とする半径 \ \dfrac{1}{2}\ の円\ C\ は \quad |z-\dfrac{1}{2}|=\dfrac{1}{2} \ \ とおけるから$

$|z-\dfrac{1}{2}|^2=\dfrac{1}{4} $

$\big(z-\dfrac{1}{2}\big)\big(\overline{z}-\dfrac{1}{2}\big)=\dfrac{1}{4} $

$z\overline{z}=\dfrac{1}{2}(z+\overline{z})$

$一般に複素数 \ \ w=p+qi \ \ の実部は \ \ p=\dfrac{1}{2}\big(w+\overline{w}\big) \ \ だから $

$\dfrac{1}{z} \ \ の実部は \quad Re\big(\dfrac{1}{z}\big)=\dfrac{1}{2}\big(\dfrac{1}{z}+\dfrac{1}{\overline{z}}\big)=\dfrac{z+\overline{z}}{2z\overline{z}}=\dfrac{z\overline{z}}{z\overline{z}}=1$


(2)


$\alpha , \ \beta \ は\ C\ 上の相異なる複素数だから(1)より\ \ \dfrac{1}{\alpha},\ \ \dfrac{1}{\beta}\ \ の実部は \ 1\ である。$

$したがって \quad \dfrac{1}{\alpha}=1+t_1i,\quad \dfrac{1}{\beta}=1+t_2 i \ \ (t_1 \ne t_2)\ \ とおける。$

$\dfrac{1}{\alpha^2}+\dfrac{1}{\beta^2}=(1+t_1i)^2+(1+t_2 i)^2=2-(t_1^2+t_2^2)+2(t_1+t_2)i$

$\dfrac{1}{\alpha^2}+\dfrac{1}{\beta^2}=x+yi \ \ (x,\ y\ は実数)\ \ とおくと$

$x=2-(t_1^2+t_2^2), \quad y=2(t_1+t_2) \ \ だから$

$t_1^2+t_2^2=2-x, \quad t_1+t_2=\dfrac{y}{2}$

$よって$
\begin{eqnarray*} t_1 t_2 &=&\dfrac{1}{2}\big((t_1+t_2)^2-(t_1^2+ t_2^2)\big)\\ \\ &=&\dfrac{1}{2}\big((\dfrac{y}{2})^2 -(2-x)\big)\\ \\ &=&\dfrac{y^2}{8}+\dfrac{x}{2}-1\\ \\ \end{eqnarray*}

　

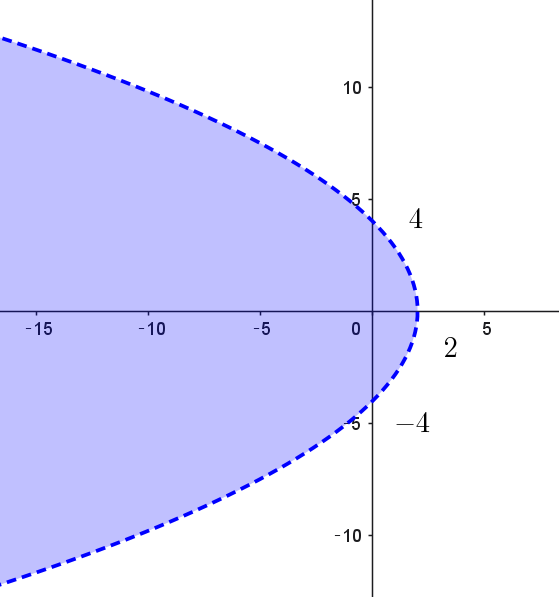
$t_1,\ t_2\ \ は \quad t^2-\dfrac{y}{2}t+\dfrac{y^2}{8}+\dfrac{x}{2}-1=0 \ \ の異なる \ 2\ つの実数解だから$

$D=\big(\dfrac{y}{2}\big)^2-4\big(\dfrac{y^2}{8}+\dfrac{x}{2}-1\big) >0$

$-\dfrac{y^2}{4}-2x+4 >0$

$\therefore x < -\dfrac{y^2}{8}+2$

$よって \quad \dfrac{1}{\alpha^2}+\dfrac{1}{\beta^2}\ \ がとりうる範囲は右図のとおりで境界は含まない。$


(3)


$\gamma=x+yi \ \ (x,\ y \ は実数)\ \ は(2)で求めた範囲に属さない複素数だから $

$x \geqq -\dfrac{y^2}{8}+2 \quad すなわち \quad y^2 \geqq -8x+16 \ \ を満たす。$

$このとき \quad \dfrac{1}{\gamma}=\dfrac{1}{x+yi}=\dfrac{x}{x^2+y^2}-\dfrac{y}{x^2+y^2}i \ \ の実部 \ X\ は$

$X=\dfrac{x}{x^2+y^2}$

(i)$\ \ x \geqq 0 \quad のとき$

$\quad X=\dfrac{x}{x^2+y^2} \leqq \dfrac{x}{x^2+(-8x+16)}=\dfrac{x}{(x-4)^2} $

(ii)$\ \ x \leqq 0 \quad のとき$

$\quad X=\dfrac{x}{x^2+y^2} \geqq \dfrac{x}{x^2+(-8x+16)}=\dfrac{x}{(x-4)^2}$

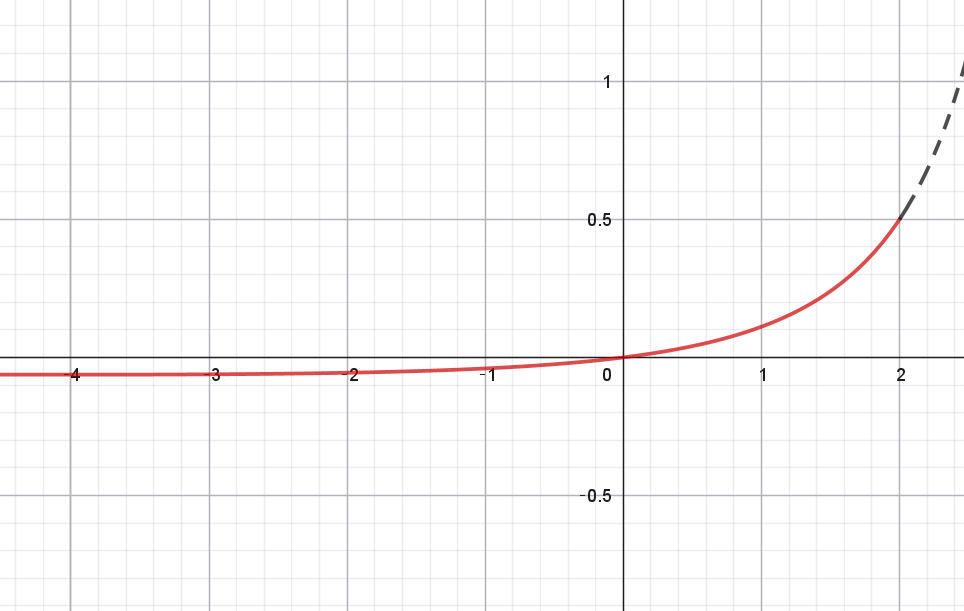
$ここで　\quad f(x)=\dfrac{x}{(x-4)^2}\ \ (x \leqq 2)\ \ とおくと$

$f'(x)=\dfrac{(x-4)^2-x \times 2(x-4)}{(x-4)^4}=\dfrac{(x-4)-2x}{(x-4)^3}=-\dfrac{x+4}{(x-4)^3}$

　

$増減表$
\[ \begin{array}{c||c|c|c|c|c} x& \cdots & -4 & \cdots & 2 \\ \hline f'(x) & - & 0 & + \\ \hline f(x) & \searrow & 極小 & \nearrow \\ \end{array} \]
$x \longrightarrow - \infty \ \ のとき \quad f(x) \longrightarrow 0$

$x=-4 \ \ のとき極小値$

$f(-4)=\dfrac{-4}{(-4-4)^2}=-\dfrac{1}{16}$

$x=2 \ \ のとき \quad f(2)=\dfrac{2}{(2-4)^2}=\dfrac{1}{2}$

$なお、f(x)\ のグラフは右図のとおり$

$したがって \quad \dfrac{1}{\gamma} \ \ の実部 \ X\ がとりうる値の$

$最大値は \quad X=\dfrac{1}{2}\ \ で、このとき \ \ x=2,\ \ y=0\ \ だから \quad \gamma=2$

$最小値は \quad X=-\dfrac{1}{16}\ \ で、このとき x=-4,\ \ y^2=-8 \times (-4)+16=48 \quad y=\pm 4\sqrt{3}\ \ だから \quad \gamma=-4 \pm 4\sqrt{3}i$


ページの先頭へ↑




メインメニュー　に戻る