東京大学(理系) 2025年 問題3
$平行四辺形 \ ABCD\ において、\angle ABC=\dfrac{\pi}{6},\ \ AB=a,\ \ BC=b,\ \ a \leqq b \ \ とする。次の条件を満たす$
$長方形 \ EFGH \ を考え、その面積を \ S\ とする。$
$\quad 条件:点 \ A,\ B.\ C.\ D\ はそれぞれ辺 \ EF,\ FG,\ GH,\ HE\ 上にある。ただし、辺はその両端の点も$
$\quad 含むものとする。$
$(1)\ \ \angle BCG=\theta \ \ とするとき、S\ を \ a,\ b,\ \theta \ \ を用いて表せ。$
$(2)\ \ S\ のとりうる値の最大値を \ a,\ b\ を用いて表せ。$
(1)
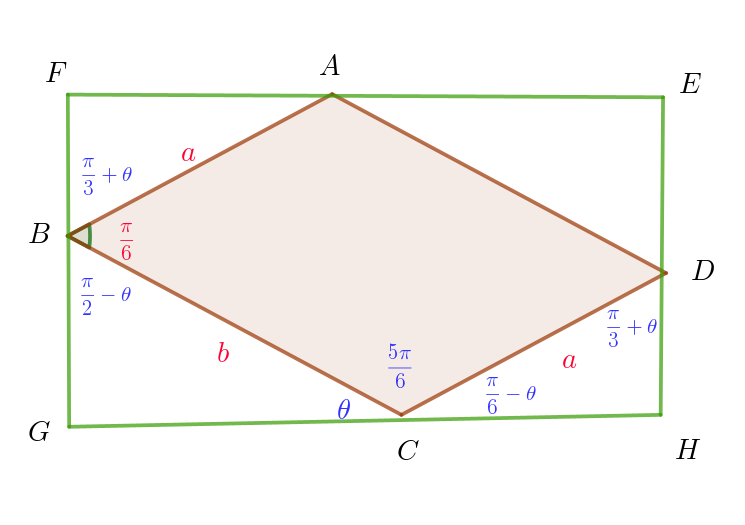
$\angle ABF=\pi -(\dfrac{\pi}{2}-\theta)-\dfrac{\pi}{6}=\dfrac{\pi}{3}+\theta$
$\angle BCD=\pi -\dfrac{\pi}{6}=\dfrac{5\pi}{6}$
$\angle DCH=\pi -\theta -\dfrac{5\pi}{6}=\dfrac{\pi}{6}-\theta$
$\angle CDH=\dfrac{\pi}{2} -(\dfrac{\pi}{6}-\theta)=\dfrac{\pi}{3}+\theta$
\begin{eqnarray*} S &=&FG \times GH\\ \\ &=&(FB+BG) \times (GC+CH)\\ \\ &=&(a\cos (\dfrac{\pi}{3}+\theta)+b\sin \theta ) \times (b\cos \theta +a\sin (\dfrac{\pi}{3}+\theta)\\ \\ &=&ab\cos \theta \cos (\dfrac{\pi}{3}+\theta) + a^2\sin (\dfrac{\pi}{3}+\theta)\cos (\dfrac{\pi}{3}+\theta) + b^2\sin \theta \cos \theta +ab\sin \theta \sin (\dfrac{\pi}{3}+\theta)\\ \\ &=&a^2\sin (\dfrac{\pi}{3}+\theta)\cos (\dfrac{\pi}{3}+\theta) + b^2\sin \theta \cos \theta + ab\big(\cos \theta \cos (\dfrac{\pi}{3}+\theta) + \sin \theta \sin (\dfrac{\pi}{3}+\theta)\big)\\ \\ &=&\dfrac{a^2}{2}\sin (\dfrac{2\pi}{3}+2\theta) + \dfrac{b^2}{2}\sin 2\theta + ab\cos \big((\dfrac{\pi}{3}+\theta)-\theta \big)\\ \\ &=&\dfrac{a^2}{2}\sin (\dfrac{2\pi}{3}+2\theta) + \dfrac{b^2}{2}\sin 2\theta + \dfrac{ab}{2}\\ \\ &=&\dfrac{a^2}{2}\big(\sin \dfrac{2\pi}{3}\cos 2\theta+\cos \dfrac{2\pi}{3}\sin 2\theta\big)+ \dfrac{b^2}{2}\sin 2\theta + \dfrac{ab}{2}\\ \\ &=&\big(\dfrac{b^2}{2}-\dfrac{a^2}{4}\big)\sin 2\theta + \dfrac{\sqrt{3}}{4}a^2\cos 2\theta + \dfrac{ab}{2}\\ \end{eqnarray*}
(2)
$\sin 2\theta \ \ と \ \ \cos 2\theta \ \ を合成して$
$S=\sqrt{\big(\dfrac{b^2}{2}-\dfrac{a^2}{4}\big)^2+ \big(\dfrac{\sqrt{3}}{4}a^2\big)^2} \sin(2\theta + \alpha) +\dfrac{ab}{2}$
$ただし \quad \cos \alpha =\dfrac{\dfrac{b^2}{2}-\dfrac{a^2}{4}}{\sqrt{\big(\dfrac{b^2}{2}-\dfrac{a^2}{4}\big)^2+ \big(\dfrac{\sqrt{3}}{4}a^2\big)^2}} ,\qquad \sin \alpha =\dfrac{\dfrac{\sqrt{3}}{4}a^2}{\sqrt{\big(\dfrac{b^2}{2}-\dfrac{a^2}{4}\big)^2+ \big(\dfrac{\sqrt{3}}{4}a^2\big)^2}}$
$\tan \alpha =\dfrac{\dfrac{\sqrt{3}}{4}a^2}{ \dfrac{b^2}{2}-\dfrac{a^2}{4}}=\dfrac{\sqrt{3}a^2}{2b^2-a^2}$
\begin{eqnarray*} S &=&\sqrt{\dfrac{b^4}{4}-\dfrac{a^2b^2}{4}+\dfrac{a^4}{16}+\dfrac{3}{16}a^4} \sin(2\theta + \alpha) +\dfrac{ab}{2}\\ \\ &=&\sqrt{\dfrac{b^4}{4}-\dfrac{a^2b^2}{4}+\dfrac{a^4}{4}} \sin(2\theta + \alpha) +\dfrac{ab}{2}\\ \\ &=&\dfrac{\sqrt{b^4 -a^2b^2 +a^4}}{2} \sin(2\theta + \alpha) +\dfrac{ab}{2}\\ \end{eqnarray*}
$ここで、\angle DCH=\dfrac{\pi}{6}-\theta \geqq 0 \ \ より \quad 0 \leqq \theta \leqq \dfrac{\pi}{6} \qquad \quad \alpha \leqq 2\theta +\alpha \leqq \dfrac{\pi}{3} +\alpha $
(i)$\ \ \dfrac{\pi}{2} \leqq \dfrac{\pi}{3} +\alpha \ \ のとき$
$\quad \alpha \geqq \dfrac{\pi}{6}\ \ より \quad \tan \alpha \geqq \dfrac{1}{\sqrt{3}}$
$\quad \dfrac{\sqrt{3}a^2}{2b^2-a^2} \geqq \dfrac{1}{\sqrt{3}} \qquad 3a^2 \geqq 2b^2-a^2 \qquad \therefore\ \ b^2 \leqq 2a^2 $
$\quad \quad a \leqq b \leqq \sqrt{2}a \ \ のとき \quad 2\theta + \alpha =\dfrac{\pi}{2} \ \ がとれて \quad \sin(2\theta + \alpha)=1$
$\quad S\ は最大値 \quad \dfrac{\sqrt{b^2-a^2b^2+a^4}}{2} +\dfrac{ab}{2} \ \ をとる$
(ii)$\ \ b \geqq \sqrt{2}a \ \ のとき$
$\quad \alpha \leqq 2\theta + \alpha < \dfrac{\pi}{2}\ \ より \quad \sin(2\theta + \alpha ) \ \ は単調増加であるから、\alpha \ を使わず、(1)の最後の式$
$\quad S=\big(\dfrac{b^2}{2}-\dfrac{a^2}{4}\big)\sin 2\theta + \dfrac{\sqrt{3}}{4}a^2\cos 2\theta + \dfrac{ab}{2} \ \ で考えると$
$\quad \theta=\dfrac{\pi}{6}\ \ のとき最大になる。$
$このとき$
\begin{eqnarray*} S &=&\big(\dfrac{b^2}{2}-\dfrac{a^2}{4}\big)\sin \dfrac{\pi}{3} + \dfrac{\sqrt{3}}{4}a^2\cos \dfrac{\pi}{3} + \dfrac{ab}{2}\\ \\ &=&\big(\dfrac{b^2}{2}-\dfrac{a^2}{4}\big) \times \dfrac{\sqrt{3}}{2} + \dfrac{\sqrt{3}}{4}a^2 \times \dfrac{1}{2} + \dfrac{ab}{2}\\ \\ &=&\dfrac{\sqrt{3}}{4}b^2+\dfrac{1}{2}ab \end{eqnarray*}
$以上より \ S\ の最大値は$
$a \leqq b \leqq \sqrt{2}a \ \ のとき \quad \dfrac{\sqrt{b^2-a^2b^2+a^4}}{2} +\dfrac{ab}{2} $
$b > \sqrt{2}a \ \ のとき \quad \dfrac{\sqrt{3}}{4}b^2+\dfrac{1}{2}ab$
メインメニュー に戻る