東京大学(理系) 2025年　問題1


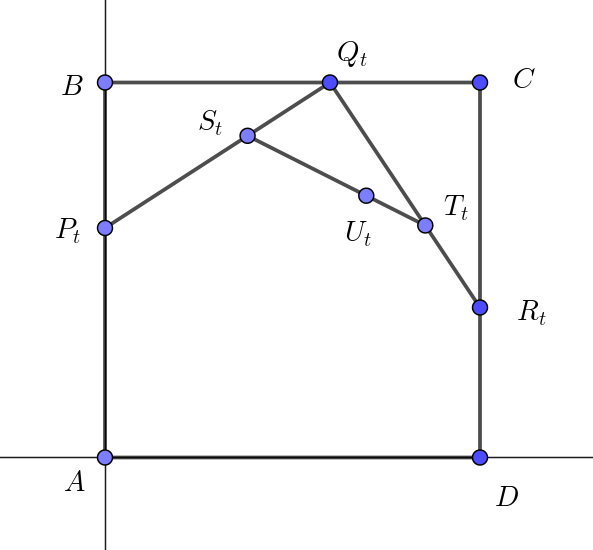
$座標平面上の点 \ A(0,\ 0),\ B(0,\ 1),\ C(1,\ 1),\ D(1,\ 0)\ \ を考える。実数 \ 0 < t < 1\ \ に対して、線分 \ AB,\ BC,$
$CD\ を \ t:(1-t)\ \ に内分する点をそれぞれ \ P_t,\ Q_t,\ R_t \ \ とし、線分 \ P_tQ_t,\ Q_tR_t\ \ を \ t:(1-t)\ \ に内分する点を$
$それぞれ \ S_t,\ T_t とする。さらに、線分 \ S_tT_t\ \ を \ t:(1-t)\ \ に内分する点を \ U_t\ とする。また、点 \ A\ を \ U_0,$
$点 \ D\ を \ U_1\ とする。$
$(1)\ \ 点 \ U_t \ の座標を求めよ。$
$(2)\ \ t\ が \ 0 \leqq t \leqq 1\ \ の範囲を動くときに点 \ U_t\ が描く曲線と、線分 \ AD\ で囲まれた部分の面積を求めよ。$
$(3)\ \ a\ を \ 0 < a < 1 \ \ を満たす実数とする。t\ が \ 0 \leqq t \leqq a \ \ の範囲を動くときに点 \ U_t\ が描く曲線の長さを、$
$\quad a\ の多項式の形で求めよ。$


(1)

　

$P_t(0,\ t),\ \ Q_t(t,\ 1),\ \ R_t(1,\ 1-t)$

$S_t((1-t) \times 0+ t \times t,\ (1-t) \times t + t \times 1)=(t^2,\ 2t-t^2)$

$T_t((1-t) \times t+ t \times 1,\ (1-t) \times 1 + t \times (1-t))=(2t-t^2,\ 1-t^2)$

$U_t(x,\ y)\ \ とおくと$

$x=(1-t) \times t^2 + t \times t(2t-t^2)=3t^2-2t^3$

$y=(1-t) \times (2t-t^2)+ t \times (1-t^2)=3t-3t^2$

$U_t(3t^2-2t^3,\ 3t-3t^2)$


(2)


$(1) より \quad x=3t^2-2t^3,\ \ y=3t-3t^2$

$\dfrac{dx}{dt}=6t-6t^2=6t(1-t)$

$\dfrac{dy}{dt}=3-6t=3(1-2t)$

　

$x,y\ の増減表は$
\[ \begin{array}{c||c|c|c|c|c} t & 0 & \cdots & \dfrac{1}{2} & \cdots & 1\\ \hline \dfrac{dx}{dt} & & + & + & + & \\ \hline \dfrac{dy}{dt} & & + & 0 & - & \\ \hline x & 0 & \nearrow & \nearrow & \nearrow & 1 \\ \hline y & 0 & \nearrow & 極大 & \searrow & 0 \\ \end{array} \] $t=0 \ \ のとき \ \ U_0(0,\ 0).\quad t=1\ \ のとき \ \ U_1(1,\ 0)$

$t=\dfrac{1}{2}\ \ のとき \quad x=\dfrac{3}{4}-\dfrac{1}{4}=\dfrac{1}{2} \ \ で$

$極大値 \ \ y=\dfrac{3}{2}-\dfrac{3}{4}=\dfrac{3}{4}\ \ をとる$

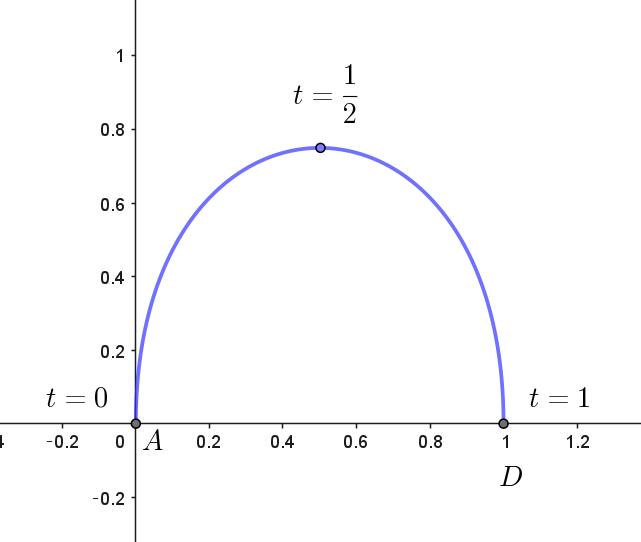
$点 \ U_t\ が描く曲線は右図のグラフである。$

$この曲線と、線分 \ AD\ で囲まれた部分の面積 \ S\ は$
\begin{eqnarray*} S &=&\int_0^1 ydx\\ \\ &=&\int_0^1(3t-3t^2)(6t-6t^2)dt\\ \\ &=&18\int_0^1(t-t^2)^2dt\\ \\ &=&18\int_0^1(t^2-2t^3+t^4)dt\\ \\ &=&18\big[\dfrac{t^3}{3}-\dfrac{t^4}{2}+\dfrac{t^5}{5}\big]_0^1\\ \\ &=&18\big(\dfrac{1}{3}-\dfrac{1}{2}+\dfrac{1}{5}\big)\\ \\ &=&\dfrac{3}{5} \end{eqnarray*}

(3)


\begin{eqnarray*} L &=&\int_0^a \sqrt{\big(\dfrac{dx}{dt}\big)^2+\big(\dfrac{dy}{dt}\big)^2}dt\\ \\ &=&\int_0^a \sqrt{(6t-6t^2)^2+ (3-6t)^2}dt\\ \\ &=&\int_0^a \sqrt{36(t-t^2)^2+ 9(1-2t)^2}dt\\ \\ &=&3\int_0^a \sqrt{4(t-t^2)^2+ (1-2t)^2}dt\\ \\ &=&3\int_0^a \sqrt{4t^4-8t^3+8t^2-4t+1}dt\\ \\ &=&3\int_0^a \sqrt{4(t^4-2t^3+t^2)+(4t^2-4t+1)}dt\\ \\ &=&3\int_0^a \sqrt{4(t^2-t)^2)+4(t^2-t)+1)}dt\\ \\ &=&3\int_0^a \sqrt{\big(2(t^2-t)+1\big)^2}dt\\ \\ &=&3\int_0^a (2t^2-2t+1)dt\\ \\ &=&3\big[\dfrac{2}{3}t^3-t^2+t\big]_0^a\\ \\ &=&3\big(\dfrac{2}{3}a^3-a^2+a\big)\\ \\ &=&2a^3-3a^2+3a \end{eqnarray*}

ページの先頭へ↑




メインメニュー　に戻る