東京大学(理系) 2024年　問題4


$f(x)=-\dfrac{\sqrt{2}}{4}x^2+4\sqrt{2} \ \ とおく。 0 < t < 4 \ \ を満たす実数 \ t\ に対し、座標平面上の点(t,\ f(t))\ を通り、$
$この点において放物線 \ y=f(x)\ と共通の接線を持ち、x\ 軸上に中心をもつ円を \ C_t \ とする。$
$(1)\ \ 円 \ C_t \ の中心の座標を(c(t),\ 0)\ ,半径を \ r(t)\ とおく。c(t)\ と \ \{r(t)\}^2\ を \ t\ の整式で表せ。$
$(2)\ \ 実数 \ a\ は \ 0 < a < f(3)\ を満たすとする、円 \ C_t \ が点(3,\ a)\ を通るような実数 \ t\ は\ 0 < t < 4 \ の範囲に$
$\quad いくつあるか。$


(1)

　

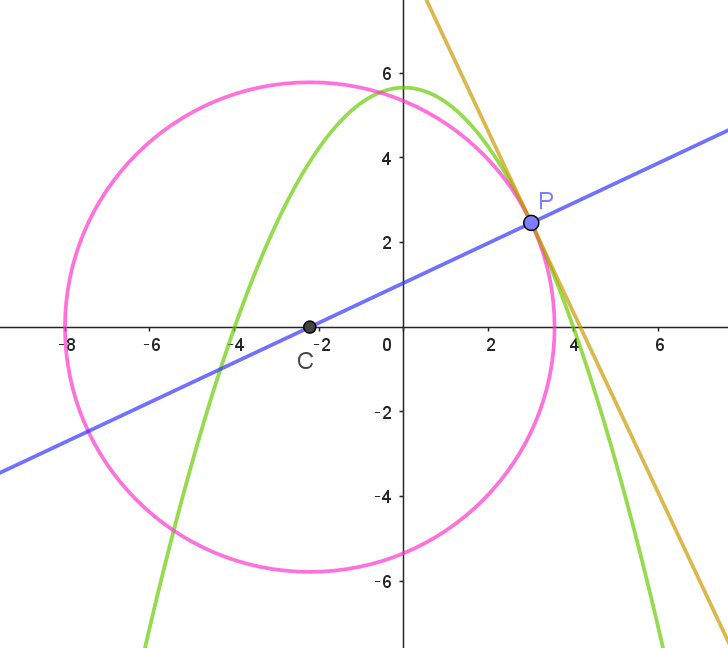
$f(x)=-\dfrac{\sqrt{2}}{4}x^2+4\sqrt{2} \ \ より \ \ f'(x)=-\cfrac{\sqrt{2}}{2}x$

$点P(t,\ f(t)) \ \ における$

$接線の傾きは \quad -\cfrac{\sqrt{2}}{2}t \quad だから$

$法線の傾きは \quad \cfrac{2}{\sqrt{2}t}=\cfrac{\sqrt{2}}{t}$

$法線の方程式は \quad y=\cfrac{\sqrt{2}}{t}(x-t)+f(t)$

$y=\cfrac{\sqrt{2}}{t}x - \sqrt{2} -\dfrac{\sqrt{2}}{4}t^2+4\sqrt{2}$

$y=\cfrac{\sqrt{2}}{t}x -\dfrac{\sqrt{2}}{4}t^2 + 3\sqrt{2}$

$円周上の点の法線はこの円の中心を通るから \ x\ 軸との交点は \ y=0\ とおいて$

$\cfrac{\sqrt{2}}{t}x -\dfrac{\sqrt{2}}{4}t^2 + 3\sqrt{2}=0$

$\cfrac{\sqrt{2}}{t}x = \dfrac{\sqrt{2}}{4}t^2 - 3\sqrt{2}$

$x=\cfrac{t}{\sqrt{2}}\big(\dfrac{\sqrt{2}}{4}t^2 - 3\sqrt{2}\big)=\cfrac{1}{4}t^3-3t$

$よって \quad c(t)=\cfrac{1}{4}t^3-3t$

\begin{eqnarray*} r(t)^2 &=&(c(t)-t)^2+\{f(t)\}^2\\ \\ &=&\big(\cfrac{1}{4}t^3-4t\big)^2+\big(-\dfrac{\sqrt{2}}{4}t^2+4\sqrt{2}\big)^2\\ \\ &=&\cfrac{t^6}{16}-2t^4+16t^2+\cfrac{t^4}{8}-4t^2+32\\ \\ &=&\cfrac{t^6}{16}-\cfrac{15}{8}t^4+12t^2+32\\ \end{eqnarray*}

(2)

　

$(1)より円 \ C_t \ の方程式は$

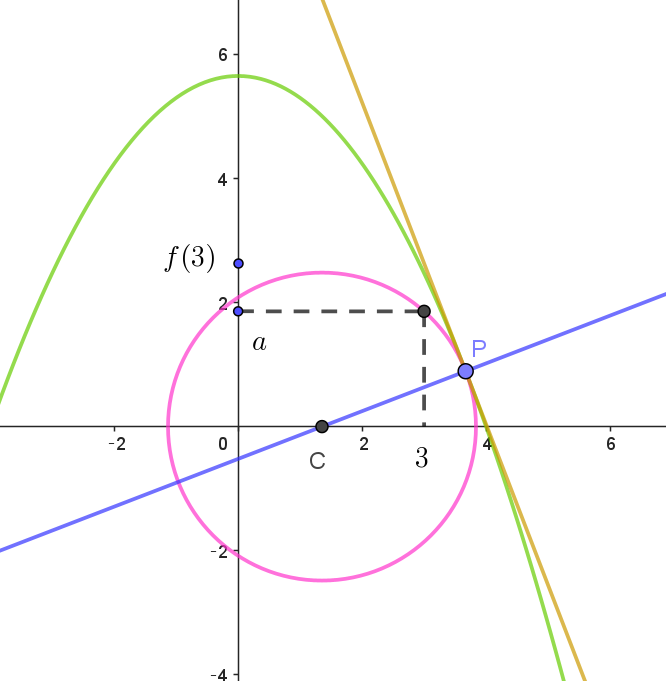
$(x-c(t))^2+y^2=\{r(t)\}^2$

$\big(x-\cfrac{1}{4}t^3+3t\big)^2+y^2=\cfrac{t^6}{16}-\cfrac{15}{8}t^4+12t^2+32$

$これが、点(3,\ a)\ を通るから$

$\big(3-\cfrac{1}{4}t^3+3t\big)^2 + a^2=\cfrac{t^6}{16}-\cfrac{15}{8}t^4+12t^2+32$

$9+\cfrac{t^6}{16}+9t^2-\cfrac{3}{2}t^3-\cfrac{3}{2}t^4+18t + a^2=\cfrac{t^6}{16}-\cfrac{15}{8}t^4+12t^2+32$

$a^2=-\cfrac{3}{8}t^4 +\cfrac{3}{2}t^3 + 3t^2-18t +23$

$これを満たす実数 \ t\ の個数を調べるために$

$y=a^2 \ と \ y=g(t)=-\cfrac{3}{8}t^4 +\cfrac{3}{2}t^3 + 3t^2-18t +23 \ \ の交点の個数を調べる。$

\begin{eqnarray*} g'(t) &=&-\cfrac{3}{2}t^3+\cfrac{9}{2}t^2+6t-18\\ \\ &=&-\cfrac{3}{2}(t^3-3t^2-4t+12)\\ \\ &=&-\cfrac{3}{2}\{t^2(t-3)-4(t-3)\}\\ \\ &=&-\cfrac{3}{2}(t+2)(t-2)(t-3)\\ \end{eqnarray*} $0 < t < 4 \ \ における増減表は$
\[ \begin{array}{c||c|c|c|c|c} t& 0 & \cdots & 2 & \cdots & 3 & \cdots & 4\\ \hline g'(t)& & - & 0 & + & 0 & - &\\ \hline g(t)& 23 & \searrow & 極小 & \nearrow & 極大 & \searrow & -1\\ \end{array} \]
$g(0)=23$

$g(4)=-\cfrac{3}{8} \times 4^4 +\cfrac{3}{2} \times 4^3 + 3 \times 4^2-18 \times 4 +23=-1$

$t=2 \ のとき極小値$

$g(2)=-\cfrac{3}{8} \times 2^4 +\cfrac{3}{2} \times 2^3 + 3 \times 2^2-18 \times 2 +23=5$

$t=3 \ のとき極大値は$

$g(3)=-\cfrac{3}{8} \times 3^4 +\cfrac{3}{2} \times 3^3 + 3 \times 3^2-18 \times 3 +23=\cfrac{49}{8}$

　

$円 \ C_t \ が点(3,\ a)\ を通るような実数 \ t\ の個数は$

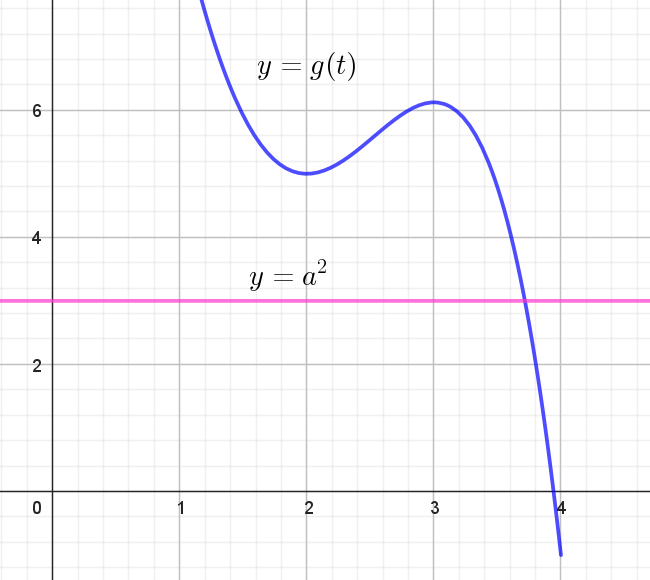
$0 < a < f(3) \ の範囲で \ \ y=a^2 \ \ と \ y=g(t)\ \ のグラフを$

$利用して交点の個数を調べればよい。$

$なお、f(3)=-\cfrac{\sqrt{2}}{4} \times 3^2+4\sqrt{2}=\cfrac{7\sqrt{2}}{4} \ \ だから$

$\{f(3)\}^2=\cfrac{49}{8} \ \ は \ g(t)\ の極大値 \ g(3)\ に等しい。$

(i)$\ \ 0 < a^2 < 5 \quad すなわち \quad 0 < a < \sqrt{5} \quad のとき \quad 1\ 個$

(ii)$\ \ a^2 = 5 \quad すなわち \quad a = \sqrt{5} \quad のとき \quad 2\ 個$

(iii)$\ \ 5 < a^2 < \cfrac{49}{8} \quad すなわち \quad \sqrt{5} < a < \cfrac{7\sqrt{2}}{4} \quad のとき　3\ 個$


ページの先頭へ↑



メインメニュー　に戻る