MY MATH NOTE

東京大学(理系) 2018年　問題5

$複素数平面上の原点を中心とする半径 \ 1\ の円を \ C\ とする。点 \ P(z)\ は \ C\ 上にあり、点 \ A(1)\ とは異なるとする。$
$点 \ P\ における円 \ C\ の接線に関して、点 \ A\ と対称な点を \ Q(u)\ とする。w=\cfrac{1}{1-u}\ とおき、w\ と共役な複素数$
$を \ \overline{w}\ で表す。$
$(1)\ \ u\ と \ \cfrac{\overline{w}}{w}\ を \ z\ についての整式として表し、絶対値の商 \ \cfrac{|w+\overline{w}-1|}{|w|}\ を求めよ。$
$(2)\ \ C\ のうち、実部が \ \cfrac{1}{2}\ 以下の複素数で表される部分を \ C'\ とする。点 \ P(z)\ が \ C'\ 上を動くときの点 \ R(w)\ の$
$\quad 軌跡を求めよ。$

(1)

　
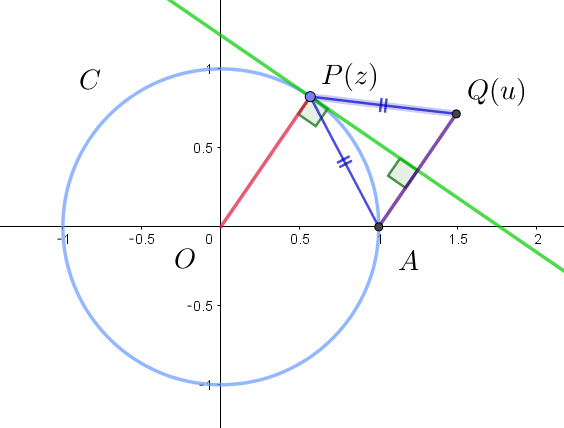
(i)$\ \ C\ は半径 \ 1\ の円だから \quad |z|=1 \hspace{6em}①$

(ii)$\ \ AQ\ /\!/ \ OP \quad より \quad u-1=kz \ \ (kは実数で \ \ k \ne 0 )\ \ とおけるから$
$\hspace{4em} u=kz+1 \hspace{14em}②$

(iii)$\ \ 点 \ P\ における円 \ C\ の接線に関して、点 \ Q(u)\ は \ A(1)\ と対称だから$
$\qquad \triangle PAQ \ \ は \ \ AP=QP\ \ の二等辺三角形である。$
$\qquad よって \quad |z-1|=|z-u|\ \hspace{9em}③$

$②を③に代入して$
$\quad |z-1|=|z-kz-1|$
$\quad |z-1|=|(1-k)z-1|$

$両辺を平方して$
$\quad (z-1)(\overline{z}-1)=\{(1-k)z-1\}\{(1-k)\overline{z}-1\}$
$\quad z\overline{z}-z-\overline{z}+1=(1-k)^2z\overline{z}-(1-k)z-(1-k)\overline{z}+1$

$①より　|z|^2=1 \quad だから \quad 　z\overline{z}=1 \quad を代入して$
$\quad 1-(z+\overline{z})+1=(1-k)^2 -(1-k)(z+\overline{z})+1$
$\quad k(z+\overline{z})=1 - (1-k)^2$
$\quad z+\overline{z} =2-k$
$\quad k=2-(z+\overline{z})$

$②に代入して$
$\quad u=\{2-(z+\overline{z})\}z+1=2z-z^2-\overline{z} z +1=2z-z^2$

$②より$
$\quad 1-u=-kz \qquad \cfrac{1}{1-u}=-\cfrac{1}{kz} \qquad w=-\cfrac{1}{kz} \qquad \overline{w}=-\cfrac{1}{k\overline{z}}$

$\quad \cfrac{\overline{w}}{w}=\cfrac{-\cfrac{1}{k\overline{z}}}{-\cfrac{1}{kz}}=\cfrac{z}{\overline{z}}=\cfrac{z^2}{z\overline{z}}=z^2$

\begin{eqnarray*} \cfrac{|w+\overline{w}-1|}{|w|} &=&\Big|1+\cfrac{\overline{w}}{w}-\cfrac{1}{w}\Big|\\ \\ &=&|1+z^2-(1-u)|\\ &=&|z^2+u|\\ &=&|z^2+(2z-z^2)|\\ &=&2|z|\\ &=&2\\ \end{eqnarray*}

(2)

　
$このとき$
$\quad z-1=p-1+qi \quad より$
$\quad |z-1|^2=(p-1)^2+q^2=p^2+q^2-2p+1=-2p+2$

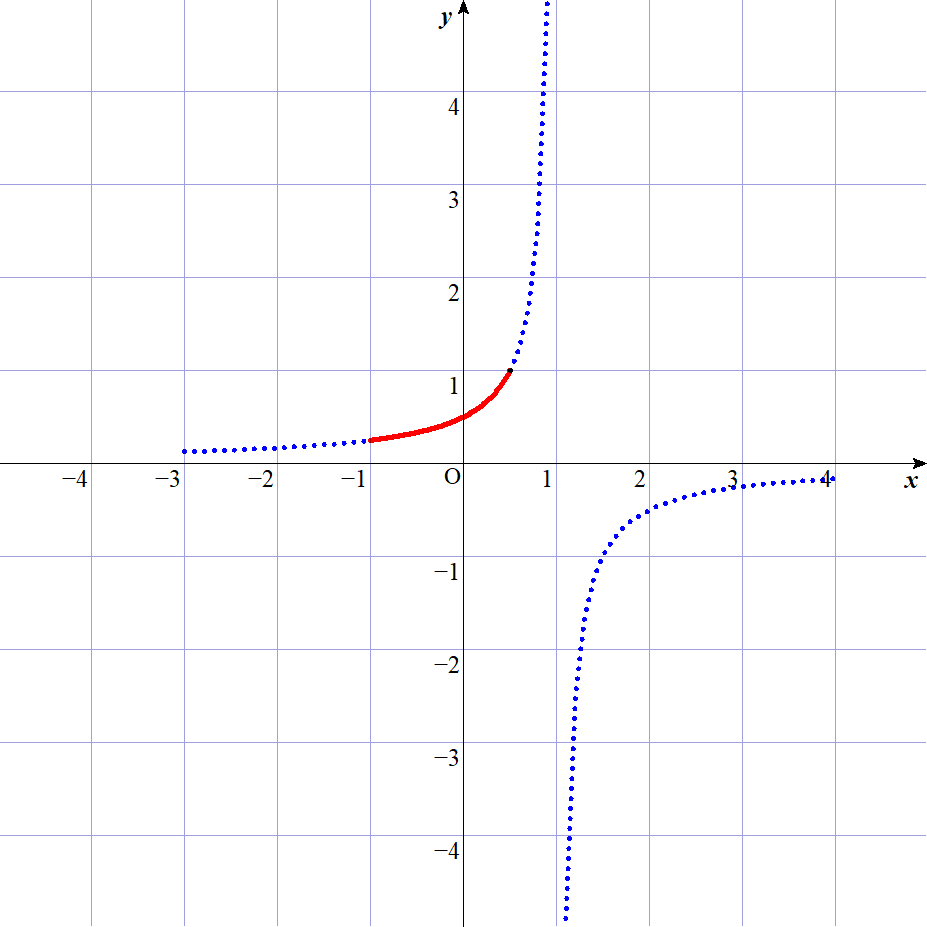
$\quad \therefore |w|=\cfrac{1}{(z-1)^2}=\cfrac{1}{-2p+2}=-\cfrac{1}{2}\cfrac{1}{p-1}$

$(p,|w|)のグラフは右のとおりで　\cfrac{1}{4} \leqq |w| \leqq 1$



$したがって R(w) の軌跡は$

　
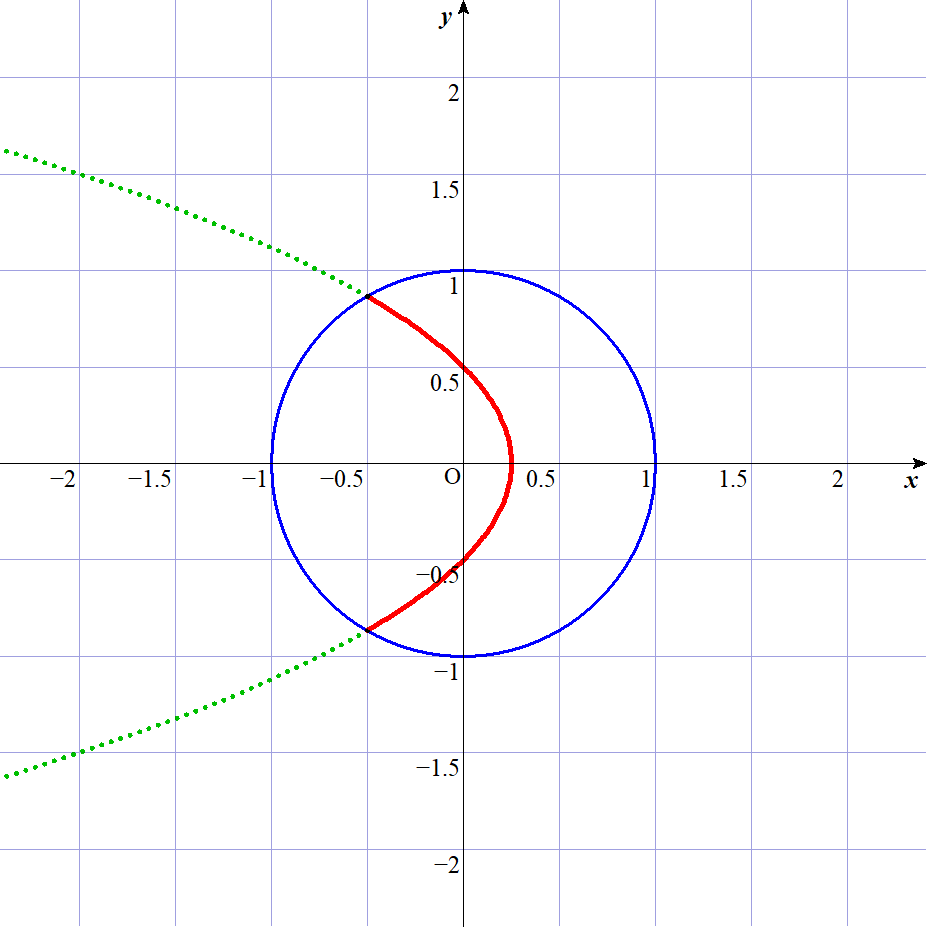
$\qquad 放物線 \quad 　x=-y^2+\cfrac{1}{4} \quad の半径1の円内$




$(2)の別解$

$(1)をつかって(2)を求めましたが、(1)を使わない解答を考えてみました。$

$|z|=1 \quad より \quad z=\cos \theta +i\sin \theta \quad とおくと$
\begin{eqnarray*} w &=&\cfrac{1}{(1-z)^2}\\ \\ &=&\Big(\cfrac{1}{1-\cos \theta - i\sin \theta }\Big)^2\\ \\ &=&\Big(\cfrac{1-\cos \theta +i\sin \theta}{(1-\cos \theta)^2+\sin ^2 \theta}\Big)^2\\ \\ &=&\Big(\cfrac{1-\cos \theta +i\sin \theta}{2(1-\cos \theta)}\Big)^2\\ \\ &=&\Big(\cfrac{2\sin ^2 \cfrac{\theta}{2}+2i\sin \cfrac{\theta}{2}\cos \cfrac{\theta}{2}}{4\sin ^2 \cfrac{\theta}{2}}\Big)^2\\ \\ &=&\Big(\cfrac{\sin \cfrac{\theta}{2}+i\cos \cfrac{\theta}{2}}{2\sin \cfrac{\theta}{2}}\Big)^2\\ \\ &=&\Big(\cfrac{i(\cos \cfrac{\theta}{2}-i\sin \cfrac{\theta}{2})}{2\sin \cfrac{\theta}{2}}\Big)^2\\ \\ &=&-\cfrac{\cos \theta -i\sin \theta }{4\sin ^2 \cfrac{\theta}{2}}\\ \end{eqnarray*}
$w=x+yi \quad とおくと$

$\quad y=\cfrac{\sin \theta}{4\sin ^2 \cfrac{\theta}{2}}=\cfrac{2\sin \cfrac{\theta}{2} \cos \cfrac{\theta}{2}}{4\sin ^2 \cfrac{\theta}{2}} =\cfrac{\cos \cfrac{\theta}{2}}{2\sin \cfrac{\theta}{2}}=\cfrac{1}{2\tan \cfrac{\theta}{2}}$

$\quad \therefore \ \ \cfrac{1}{\tan ^2 \cfrac{\theta}{2}}=4y^2$

$\quad 1+\cfrac{1}{\tan ^2 \cfrac{\theta}{2}}=\cfrac{1}{\sin ^2 \theta} \quad だから \quad \quad \cfrac{1}{\sin ^2 \theta}=1+4y^2$

$また$

$\quad x=-\cfrac{\cos \theta}{4\sin ^2 \cfrac{\theta}{2}}=-\cfrac{1-2\sin ^2 \cfrac{\theta}{2}}{4\sin ^2 \cfrac{\theta}{2}} = -\cfrac{1}{4\sin ^2 \cfrac{\theta}{2}} +\cfrac{1}{2}=-\cfrac{1}{4}(1+4y^2)+\cfrac{1}{2}$

$\quad \therefore x= \cfrac{1}{4}-y^2$

$ただし \quad x \leqq \cfrac{1}{2} \quad より \quad \cfrac{\pi}{3} \leqq \theta \leqq \cfrac{5\pi}{3} \hspace{4em} \cfrac{\pi}{6} \leqq \cfrac{\theta}{2} \leqq \cfrac{5\pi}{6}$

$したがって$

$\quad \tan \cfrac{\theta}{2} \geqq \cfrac{1}{\sqrt{3}} \quad より \qquad 0 < \cfrac{1}{2\tan \cfrac{\theta}{2}} \leqq \cfrac{\sqrt{3}}{2} \hspace{4em} 0 < y \leqq \cfrac{\sqrt{3}}{2}$

$\quad \tan \cfrac{\theta}{2} \leqq -\cfrac{1}{\sqrt{3}} \quad より \qquad -\cfrac{\sqrt{3}}{2} \leqq \cfrac{1}{2\tan \cfrac{\theta}{2}} <0 \hspace{4em} -\cfrac{\sqrt{3}}{2} \leqq y < 0$

$なお、y=0 \quad のときは \quad x=\cfrac{1}{4} \quad だから \quad y=0 \quad も満たす。$

$よって求める軌跡は \quad x= \cfrac{1}{4}-y^2 \quad で \quad -\cfrac{\sqrt{3}}{2} \leqq y \leqq \cfrac{\sqrt{3}}{2} \quad の部分$

ページの先頭へ↑