東京大学(理系) 2018年 問題1
$関数 \ \ f(x)=\cfrac{x}{\sin x} + \cos x \ \ (0 < x < \pi)\ の増減表をつくり、x \rightarrow +0,\ \ x \rightarrow \pi -0 \ \ のときの極限を調べよ。$
$(解説)$
$問題としてはとくに難しいところはありません。増減表をつくらせるところにどのような意味があるかわかりません。$
$グラフをかかせるのであればわかるのですが \cdots$
$f'(x)=\cfrac{\sin x -x\cos x }{\sin ^2 x}-\sin x=\cfrac{\sin x -x\cos x -\sin ^3 x}{\sin ^2 x}$
$f'(x)\ の分子を \ g(x)\ とおくと$
\begin{eqnarray*} g(x) &=&\sin x -x\cos x -\sin ^3 x\\ &=&\sin x -x\cos x -\sin x(1-\cos ^2 x)\\ &=&-x\cos x + \sin x \cos ^2 x\\ &=&-\cos x (x- \sin x \cos x)\\ &=&-\cos x (x- \cfrac{1}{2}\sin 2x )\\ \end{eqnarray*} $\qquad h(x)=x- \cfrac{1}{2}\sin 2x \quad とおくと$
$\qquad h'(x)=1-\cos 2x > 0 \quad だから \quad h(x) \ は区間 \ (0,\ \pi)\ で単調増加 \qquad よって \quad h(x) > h(0)=0 $
$g(x)=0 \quad すなわち \quad f'(x)=0 \quad より \quad \cos x=0 \qquad x=\cfrac{\pi}{2}$
$増減表は$
\[ \begin{array}{c||c|c|c|c|c} \hline x& 0 & \cdots & \dfrac{\pi}{2} & \cdots & \pi \\ \hline y'& & - & 0 & + & \\ \hline y& & \searrow & 極小 & \nearrow & \\ \hline \end{array} \]
$\qquad x=\cfrac{\pi}{2}\ \ で \ \ 極小値 \ \ f(\cfrac{\pi}{2})=\cfrac{\pi}{2}\ \ をもつ$
$\quad x \longrightarrow +0 \quad のとき$
$\qquad \cfrac{x}{\sin x}=\cfrac{1}{\cfrac{\sin x}{x}} \longrightarrow 1,\qquad \cos x \longrightarrow 1 \quad だから \quad f(x) \longrightarrow 2$
$x \longrightarrow \pi -0 \quad のとき$
$\qquad \sin x \longrightarrow +0 \quad だから \quad \cfrac{x}{\sin x} \longrightarrow +\infty \qquad \cos x \longrightarrow -1 \quad したがって \quad f(x) \longrightarrow +\infty$
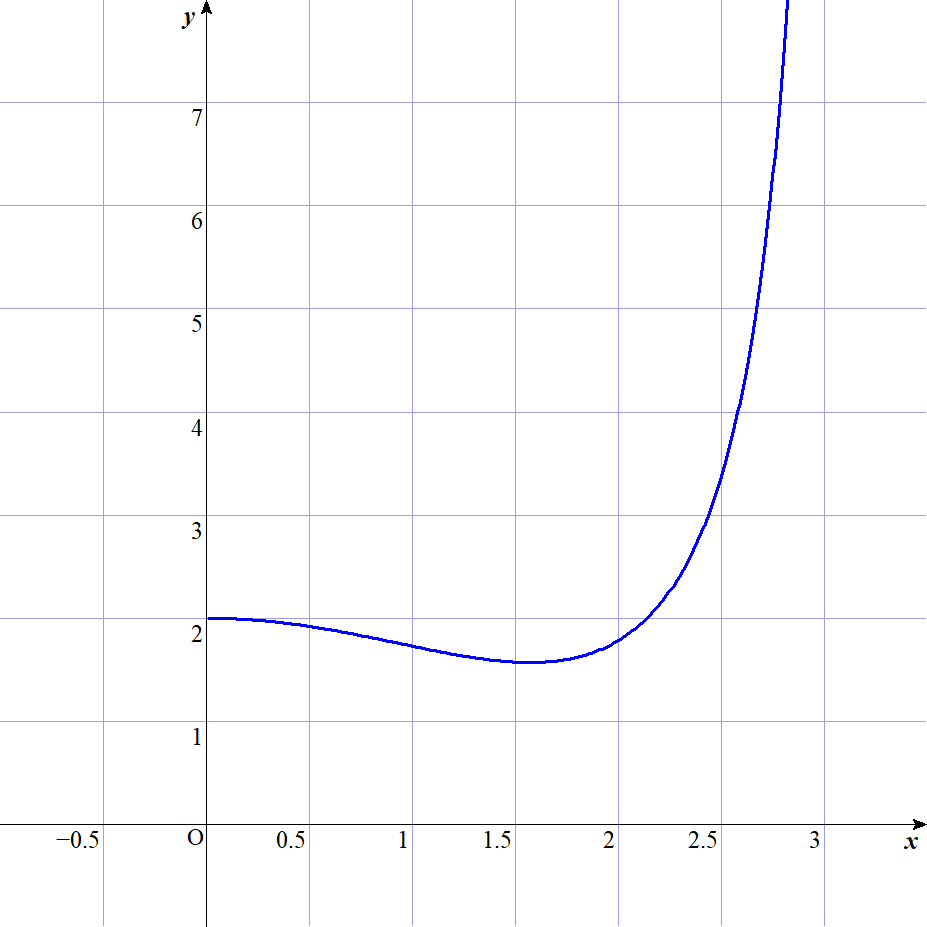
$なお、グラフは右のとおりですが$
$\qquad x \longrightarrow +0 \quad のとき \quad f'(x) \longrightarrow 0 $
$したがって、x=0 \ \ での接線は \ x\ 軸に平行となります。$
$(この極限値を求めるのは意外に大変です。 $不定形の極限値(3)$を参考にしてください。)$
メインメニュー に戻る