東京工業大学(理系) 2024年 問題3
$xy\ 平面上に、点A(a,\ 0),\ B(0,\ b),\ C(-a,\ 0) \ \ (ただし \ \ 0 < a < b)\ \ をとる。点 \ A,\ B\ を通る直線を \ \ell \ とし、$
$点 \ C\ を通り線分 \ BC\ に垂直な直線を \ k\ とする。さらに、点 \ A\ を通り \ y\ 軸に平行な直線と直線 \ k\ との交点を$
$C_1\ とし、点 \ C_1\ を通り \ x\ 軸に平行な直線と直線 \ \ell \ の交点を \ A_1\ とする。以下、n=1,\ 2,\ 3,\ \cdots \ に対して、$
$点 \ A_n\ を通り \ y\ 軸に平行な直線と直線 \ k\ との交点を \ C_{n+1},\ 点 \ C_{n+1}\ を通り \ x\ 軸に平行な直線と直線 \ \ell \ の交点を$
$A_{n+1}\ とする。$
$(1)\ \ 点 \ A_n,\ C_n \ の座標を求めよ。$
$(2)\ \ \triangle CBA_n の面積 \ S_n\ を求めよ。$
\[(3)\ \ \lim _{n \rightarrow \infty} \dfrac{BA_n}{BC}\ \ を求めよ。\]
(1)
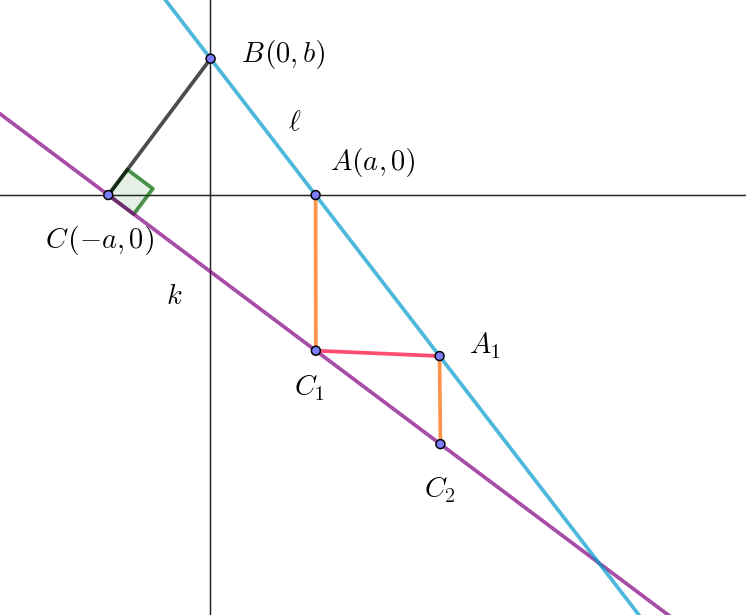
$線分BC の傾き=\cfrac{b}{a}\ \ だから \ \ 直線 \ k : y=-\cfrac{a}{b}(x+a)$
$点C_1 \ の \ y\ 座標は直線 \ k\ と \ x=a\ の交点だから$
$y=-\cfrac{a}{b} \times (a+a)=-\cfrac{2a^2}{b}$
$C_1(a,\ -\cfrac{2a^2}{b}) $
$点A_1\ の \ x\ 座標は直線 \ \ell\ と \ y=-\cfrac{2a^2}{b}\ \ の交点だから$
$-\cfrac{2a^2}{b}=-\cfrac{b}{a}x+b \qquad x=\cfrac{a(b^2+2a^2)}{b^2}$
$A_1(\cfrac{a(b^2+2a^2)}{b^2},\ -\cfrac{2a^2}{b}) $
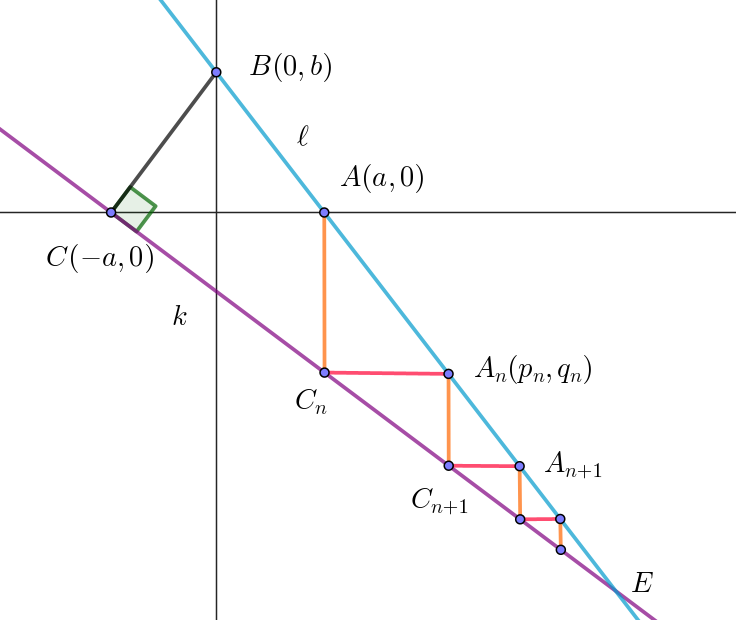
$C_n\ の \ y\ 座標は \ q_n,\ \ C_{n+1}\ の \ x\ 座標は \ p_n\ だから$
$C_n(p_{n-1},\ q_n), \quad C_{n+1}(p_n,\ q_{n+1})\ \ とおける。$
$A_n(p_n,\ q_n)\ は \ \ell \ 上の点だから$
$\quad q_n=-\cfrac{b}{a}p_n +b \hspace{6em}①$
$C_{n+1}(p_n,\ q_{n+1}) \ は k\ 上の点だから$
$\quad q_{n+1}=-\cfrac{a}{b}(p_n +a) \hspace{5em}②$
$①を②に代入して$
$-\cfrac{b}{a}p_{n+1} +b=-\cfrac{a}{b}(p_n +a)$
$p_{n+1}=\cfrac{a^2}{b^2}p_n+\cfrac{a(b^2+a^2)}{b^2} \hspace{8em}③$
$特性方程式 \quad t=\cfrac{a^2}{b^2}t+\cfrac{a(b^2+a^2)}{b^2} \hspace{5em}④$
$これを解いて \quad t=\cfrac{a(b^2+a^2)}{b^2-a^2}$
$③-④より$
$p_{n+1}-t=\cfrac{a^2}{b^2}(p_n -t)$
$p_n-t=(p_1-t)\big(\dfrac{a^2}{b^2}\big)^{n-1}$
\begin{eqnarray*} p_n &=&\cfrac{a(b^2+a^2)}{b^2-a^2}+\big(\cfrac{a(b^2+2a^2)}{b^2}-\cfrac{a(b^2+a^2)}{b^2-a^2}\big)\big(\dfrac{a^2}{b^2}\big)^{n-1}\\ \\ &=&\cfrac{a(b^2+a^2)}{b^2-a^2}+a \big(\cfrac{(b^2+2a^2)(b^2-a^2)-b^2(b^2+a^2)}{b^2(b^2-a^2)}\big)\big(\dfrac{a^2}{b^2}\big)^{n-1}\\ \\ &=&\cfrac{a(b^2+a^2)}{b^2-a^2} - \cfrac{2a^5}{b^2(b^2-a^2)}\big(\dfrac{a^2}{b^2}\big)^{n-1}\\ \\ &=&\cfrac{a(b^2+a^2)}{b^2-a^2} - \cfrac{2a^3}{b^2-a^2}\big(\dfrac{a}{b}\big)^{2n}\\ \end{eqnarray*} \begin{eqnarray*} q_n &=&-\cfrac{b}{a}p_n+b\\ \\ &=&-\cfrac{b}{a}\Big(\cfrac{a(b^2+a^2)}{b^2-a^2} - \cfrac{2a^3}{b^2-a^2}\big(\dfrac{a}{b}\big)^{2n}\Big)+b\\ \\ &=&b-\cfrac{b(b^2+a^2)}{b^2-a^2} + \cfrac{2a^2b}{b^2-a^2}\big(\dfrac{a}{b}\big)^{2n}\\ \\ &=&-\cfrac{2a^2b}{b^2-a^2} + \cfrac{2a^2b}{b^2-a^2}\big(\dfrac{a}{b}\big)^{2n}\\ \end{eqnarray*}
$よって$
$A_n(\cfrac{a(b^2+a^2)}{b^2-a^2} - \cfrac{2a^3}{b^2-a^2}\big(\dfrac{a}{b}\big)^{2n}, \ -\cfrac{2a^2b}{b^2-a^2} + \cfrac{2a^2b}{b^2-a^2}\big(\dfrac{a}{b}\big)^{2n})$
$C_n(\cfrac{a(b^2+a^2)}{b^2-a^2} - \cfrac{2a^3}{b^2-a^2}\big(\dfrac{a}{b}\big)^{2(n-1)}, \ -\cfrac{2a^2b}{b^2-a^2} + \cfrac{2a^2b}{b^2-a^2}\big(\dfrac{a}{b}\big)^{2n})$
(2)
$点A_n(p_n,\ q_n) \ から直線 \ BC\ に下した垂線を \ A_nD\ とすると$
$BC \ :\ y=\cfrac{b}{a}x+b \ \ より \ \ bx-ay+ab=0$
$点A_n(p_n,\ q_n)\ はこの直線の下側にあるから \quad y < \cfrac{b}{a}x+ b \ \ すなわち \ \ bx-ay+ab > 0 \ \ をみたす。$
$したがって \quad A_nD=\cfrac{|bp_n-aq_n+ab|}{\sqrt{b^2+a^2}}=\cfrac{bp_n-aq_n+ab}{\sqrt{b^2+a^2}}$
\begin{eqnarray*} S_n &=&\cfrac{1}{2} \times BC \times A_nD\\ \\ &=&\cfrac{1}{2} \times \sqrt{b^2+a^2} \times \cfrac{bp_n-aq_n+ab}{\sqrt{b^2+a^2}}\\ \\ &=&\cfrac{1}{2}(bp_n-aq_n+ab)\\ \\ &=&\cfrac{1}{2}\Big\{b \Big(\cfrac{a(b^2+a^2)}{b^2-a^2} - \cfrac{2a^3}{b^2-a^2}\big(\dfrac{a}{b}\big)^{2n}\Big) -a\Big(-\cfrac{2a^2b}{b^2-a^2} + \cfrac{2a^2b}{b^2-a^2}\big(\dfrac{a}{b}\big)^{2n}\Big)+ab \Big\}\\ \\ &=&\cfrac{ab}{2}\big(\cfrac{b^2+a^2}{b^2-a^2} + \cfrac{2a^2}{b^2-a^2} + 1\big) - \Big(\cfrac{a^3b}{b^2-a^2} + \cfrac{a^3b}{b^2-a^2}\big)\big(\dfrac{a}{b}\big)^{2n}\\ \\ &=&\cfrac{ab(b^2+a^2)}{b^2-a^2} - \cfrac{2a^3b}{b^2-a^2} \big(\dfrac{a}{b}\big)^{2n}\\ \end{eqnarray*}
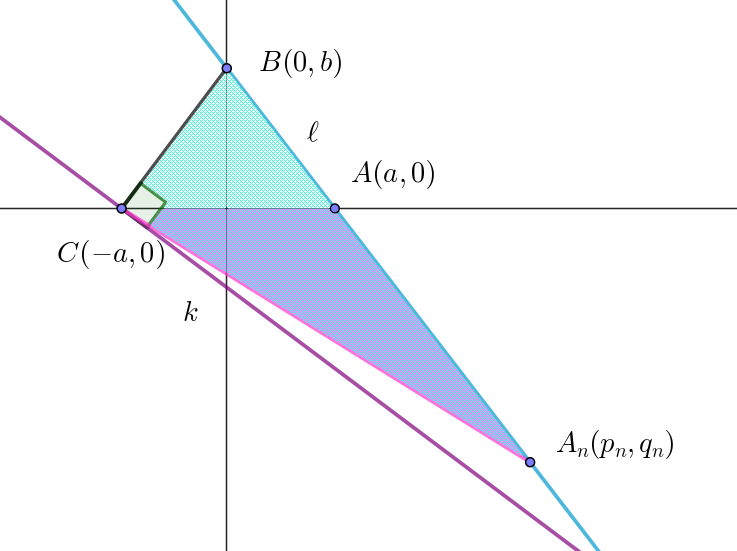
\begin{eqnarray*} & &\triangle CBA_n\\ \\ &=&\triangle CBA + \triangle CA_nA\\ \\ &=&\cfrac{1}{2} \times AC \times (B\ の \ y\ 座標)+\cfrac{1}{2} \times AC \times (A_n \ の \ |y座標|)\\ \\ &=&\cfrac{1}{2} \times AC \times (B\ の \ y\ 座標)+(A_n\ の \ |y座標|))\\ \\ &=&\cfrac{1}{2} \times 2a \times (b-q_n))\\ \\ &=&a \times (b+\cfrac{2a^2b}{b^2-a^2} - \cfrac{2a^2b}{b^2-a^2}\big(\dfrac{a}{b}\big)^{2n})\\ \\ &=&\cfrac{ab(b^2+a^2)}{b^2-a^2} - \cfrac{2a^3b}{b^2-a^2} \big(\dfrac{a}{b}\big)^{2n}\\ \end{eqnarray*}
(3)
$点A_n(p_n,\ q_n)\ は \ \ell \ 上にあるから \quad q_n=b(1-\cfrac{p_n}{a})$
\begin{eqnarray*} BA_n^2 &=&p_n^2+(q_n-b)^2\\ \\ \\ &=&p_n^2+(-\dfrac{b}{a}p_n)^2\\ \\ &=&(1+\dfrac{b^2}{a^2})p_n^2\\ \\ &=&\cfrac{b^2+a^2}{a^2} \big(\cfrac{a(b^2+a^2)}{b^2-a^2} - \cfrac{2a^3}{b^2-a^2}\big(\dfrac{a}{b}\big)^{2n} \big)^2\\ \\ &=&\cfrac{b^2+a^2}{a^2} \times \big(\cfrac{a}{b^2-a^2}\big)^2\big((b^2+a^2) - 2a^2 \big(\dfrac{a}{b}\big)^{2n} \big)^2\\ \\ &=&\cfrac{b^2+a^2}{(b^2-a^2)^2} \big(b^2+a^2- 2a^2 \big(\dfrac{a}{b}\big)^{2n} \big)^2\\ \end{eqnarray*}
$よって$
$\cfrac{BA_n}{BC}=\cfrac{\sqrt{b^2+a^2}}{b^2-a^2} \big|b^2+a^2- 2a^2 \big(\dfrac{a}{b}\big)^{2n} \big| \times \cfrac{1}{\sqrt{b^2+a^2}}=\cfrac{1}{b^2-a^2} \big|b^2+a^2- 2a^2 \big(\dfrac{a}{b}\big)^{2n} \big|$
$0 < a < b \ \ だから \quad 0 < \cfrac{a}{b}< 1$
$したがって \quad n \longrightarrow \infty \quad のとき \quad (\cfrac{a}{b})^n \longrightarrow 0$
\[\therefore \lim_{n \rightarrow \infty} \cfrac{BA_n}{BC}=\cfrac{b^2+a^2}{b^2-a^2}\]
$(別解)$
$(1)より \ \ A_n(p_n,\ q_n)\ は \ \ p_n=\cfrac{a(b^2+a^2)}{b^2-a^2} - \cfrac{2a^3}{b^2-a^2}\big(\dfrac{a}{b}\big)^{2n},\qquad q_n=-\cfrac{2a^2b}{b^2-a^2} + \cfrac{2a^2b}{b^2-a^2}\big(\dfrac{a}{b}\big)^{2n}$
$n \longrightarrow \infty \ \ のとき \quad p_n \longrightarrow \cfrac{a(b^2+a^2)}{b^2-a^2} ,\qquad q_n \longrightarrow -\cfrac{2a^2b}{b^2-a^2} $
$点列 \ \{A_n\} \ の極限を A_{\infty} \ \ とおくと \quad A_{\infty}(\cfrac{a(b^2+a^2)}{b^2-a^2} , \ -\cfrac{2a^2b}{b^2-a^2}) $
$したがって$
$BA_{\infty}^2=\big(\cfrac{a(b^2+a^2)}{b^2-a^2}\big)^2+\big(-\cfrac{2a^2b}{b^2-a^2}-b\big)^2= \big(\cfrac{a(b^2+a^2)}{b^2-a^2}\big)^2+\big(\cfrac{b(b^2+a^2)}{b^2-a^2}\big)^2=\cfrac{(b^2+a^2)^3}{(b^2-a^2)^2}$
\[\lim _{n \rightarrow \infty} \cfrac{BA_n}{BC}=\cfrac{BA_{\infty}}{BC}=\cfrac{1}{\sqrt{b^2+a^2}} \times \cfrac{(b^2+a^2)\sqrt{b^2+a^2}}{b^2-a^2}=\cfrac{b^2+a^2}{b^2-a^2}\]
$(補充)$
$\ell : y=-\cfrac{b}{a}x+b \ と \ k: y=-\cfrac{a}{b}(x+a)\ の交点 \ E\ は$
$-\cfrac{b}{a}x+b=-\cfrac{a}{b}(x+a)$
$(\cfrac{b}{a}-\cfrac{a}{b})x=b+\cfrac{a^2}{b}$
$\cfrac{b^2-a^2}{ab}x=\cfrac{b^2+a^2}{b}$
$x=\cfrac{a(b^2+a^2)}{b^2-a^2}$
$y=-\cfrac{b}{a} \times \cfrac{a(b^2+a^2)}{b^2-a^2}+b=-\cfrac{2a^2b}{b^2-a^2}$
$したがって\ \ 交点 \ E\ が \ \ A_{\infty}\ になります。$
メインメニュー に戻る