東京工業大学(理系) 2024年 問題2
$実数全体を定義域にもつ微分可能な関数 \ f(t),\ g(t)\ が次の \ 6\ つの条件を満たしているとする。$
$\quad f'(t)=-f(t)g(t), \quad g'(t)=\{f(t)\}, \quad f(t) > 0,\quad |g(t)|<1, \quad f(0)=1,\quad g(0)=0$
$このとき、p(t)=\{f(t)\}^2+\{g(t)\}^2,\quad q(t)=\log \dfrac{1+g(t)}{1-g(t)} \quad とおく。$
$(1)\ \ p'(t) \ \ を求めよ。$
$(2)\ \ q'(t) \ \ は定数関数であることを示せ。\ \ $
\[(3)\ \ \lim _{t \rightarrow \infty} g(t) \ \ を求めよ。\]
$(4)\ \ f(T)=g(T) \ \ となる正の実数 \ T\ に対して、媒介変数表示された平面曲線$
$\quad (x,\ y)=(f(t),\ g(t)) \ \ (0 \leqq t \leqq T)\ \ の長さを求めよ。$
$f(t),\ \ g(t),\ \ \{f(t)\}^2, \ \ \{g(t)\}^2 \ \ を単に \ f,\ g,\ f^2,\ g^2\ \ と表すこととする。$
(1)
$p(t)=f^2+ g^2 \ \ より$
\begin{eqnarray*} p'(t) &=&2ff'+2gg'\\ \\ &=&2f(-fg)+2gf^2\\ \\ &=&-2f^2g+2f^2g\\ \\ &=&0 \end{eqnarray*}
(2)
$まず$
$p'(t)=0 \ \ より \ \ p(t)=C \ \ (定数)\ \ とおける。$
$P(0)=f(0)^2+g(0)^2=1 \quad だから \quad C=1$
$よって \quad p(t)=f^2+g^2=1$
$次に$
$q(t)=\log \dfrac{1+g}{1-g}=\log (1+g)- \log (1-g) \quad より$
\begin{eqnarray*} q'(t) &=&\cfrac{g'}{1+g}+\cfrac{g'}{1-g}\\ \\ &=&\cfrac{g'(1-g)+g'(1+g)}{(1+g)(1-g)}\\ \\ &=&\cfrac{2g'}{1-g^2}\\ \\ &=&\cfrac{2f^2}{1-g^2}\\ \\ &=&\cfrac{2f^2}{f^2}\\ \\ &=&2 \end{eqnarray*}
$よって、q'(t) \ \ は定数関数である。$
(3)
$(2)より \quad q'(t)=2 \ \ (定数)\ \ だから \quad q(t)=2t+m \ \ (m\ は定数) \ \ とおける。$
$ところが、q(0)=\log \dfrac{1+g(0)}{1-g(0)}=\log 1=0 \quad だから \quad m=0$
$\therefore \ \ q(t)=2t$
$よって \quad q(t)=\log \dfrac{1+g}{1-g} =2t $
$\cfrac{1+g}{1-g} =e^{2t} $
$-1 + \cfrac{2}{1-g} =e^{2t} $
$\cfrac{2}{1-g} =1+e^{2t} $
$1-g =\cfrac{2}{1+e^{2t}} $
$g =1-\cfrac{2}{1+e^{2t}} $
\[\lim _{t \rightarrow \infty} g(t) =\lim _{t \rightarrow \infty} (1-\cfrac{2}{1+e^{2t}})= 1\]
(4)
$(2)より \quad f^2+g^2=1 \quad だから \quad t=Tとおいて \quad f(T)^2+g(T)^2=1$
$f(T)=g(T) \ \ となる \ T\ は \quad 2f(T)^2=1 \quad f(T)^2=\cfrac{1}{2} \quad f(t) > 0 \ \ だから \quad f(T)=g(T)=\cfrac{1}{\sqrt{2}}$
$媒介変数表示された平面曲線 \ \ (x,\ y)=(f(t),\ g(t))\ \ は \ \ f^2+g^2=1 \quad だから 原点中心、半径 \ 1\ の円を描く。$
$ただし \quad f(t) > 0,\quad |g(t)| < 1\ \ だから この円の右半分である。$
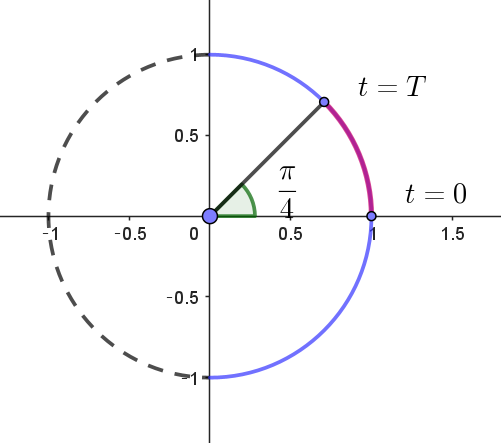
$t=0 \quad のとき \quad f(0)=1,\quad g(0)=0 \quad より \quad (x,\ y)=(1,\ 0)$
$t=T \quad のとき \quad f(T)=g(T)=\cfrac{1}{\sqrt{2}}$
$求める長さ \ L\ は \quad L=1 \times \cfrac{\pi}{4}=\cfrac{\pi}{4}$
$(研究)$
$問題は \ f(t),\ \ g(t)\ に関する連立微分方程式と初期条件が与えられているだけです。$
$f(t),\ g(t)\ \ から作られた \ p(t),\ q(t)\ を手がかりに \ f(t),\ g(t)\ の性質を導く問題となっています。$
$(Ⅰ) \quad f(t),\ g(t)\ \ を \ t\ の関数として具体的に求めてみましょう。$
$(3)で \ \ g(t) =1-\cfrac{2}{1+e^{2t}} \quad を導きましたが、これを変形して$
$g(t)=\cfrac{e^{2t}-1}{e^{2t}+1}=\cfrac{e^t-e^{-t}}{e^t+e^{-t}}$
$(2)で求めた \quad f^2+g^2=1 \quad より$
\begin{eqnarray*}
f^2
&=&1-g^2\\
\\
&=&1-\big(1-\cfrac{2}{1+e^{2t}}\big)^2\\
\\
&=&\cfrac{4}{1+e^{2t}}- \cfrac{4}{(1+e^{2t})^2}\\
\\
&=&\cfrac{4e^{2t}}{(1+e^{2t})^2}\\
\end{eqnarray*}
$f > 0\ \ だから \quad f(t)=\cfrac{2e^{t}}{1+e^{2t}}=\cfrac{2}{e^t+e^{-t}}$
$これで、具体的な関数として \ f(t),\ \ g(t)\ \ が求まりましたが。一般に$
$\cfrac{e^t+e^{-t}}{2} =\cosh t ,\qquad \cfrac{e^t-e^{-t}}{2} =\sinh t ,\qquad \cfrac{\sinh t}{\cosh t}=\tanh t $
$と表し、$双曲線関数$といいます。$
$\cosh^2 t - \sinh ^2 t =1,\quad (\sinh t)'=\cosh t ,\quad (\cosh t)'=\sinh t$
$などの性質が簡単に導かれます。$
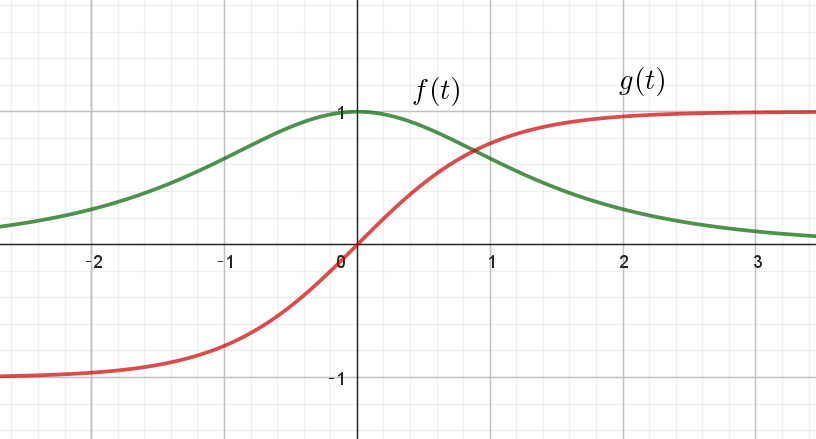
$f(t)=\cfrac{2}{e^t+e^{-t}}=\cfrac{1}{\cosh t} ,\qquad g(t)=\cfrac{e^t-e^{-t}}{e^t+e^{-t}}=\tanh t $
$だったわけです。$
$f(t),\ \ g(t)\ \ のグラフは右図のとおりです。$
$(Ⅱ) \quad 曲線の長さを公式を使って求めてみましょう。$
\begin{eqnarray*}
L
&=&\int_0^T \sqrt{\big(\dfrac{df}{dt}\big)^2+\big(\dfrac{dg}{dt}\big)^2}dt\\
\\
&=&\int_0^T \sqrt{(-fg)^2+ (f^2)^2}dt\\
\\
&=&\int_0^T f\sqrt{ g^2+ f^2}dt\\
\\
&=&\int_0^T fdt\\
\\
&=&\int_0^T \cfrac{dt}{\cosh t}\\
\\
&=&\int_0^T \cfrac{\cosh t}{\cosh^2 t}dt\\
\\
&=&\int_0^T \cfrac{\cosh t}{1+\sinh^2 t}dt\\
\end{eqnarray*}
$f(T)=\cfrac{1}{\cosh T} ,\quad g(T)=\tanh T=\cfrac{\sinh T}{\cosh T} $
$f(T)=g(T) \ \ より \ \ \cfrac{1}{\cosh T}=\cfrac{\sinh T}{\cosh T} \qquad \therefore \ \ \sinh T=1$
\[
\sinh t=u \quad とおくと \quad \cosh t \ dt=du
\qquad
\begin{array}{c|c}
t & 0\ \ \rightarrow T \\
\hline
u & 0\ \ \rightarrow 1 \\
\end{array}
\]
\[L=\int_0^1 \cfrac{du}{1+u^2}=\big[\tan ^{-1} u\big]_0^1=\cfrac{\pi}{4}\]
$(Ⅲ) \quad 連立微分方程式を直接解いてみましょう。$
\[
\hspace{1em}
\left\{ \begin{array}{l}
f'=-fg \hspace{5em}①\\
g'=f^2 \hspace{6em}②\\
\end{array} \right.
\]
$②の両辺を\ t\ で微分して$
\begin{eqnarray*}
g''
&=&2ff'\\
\\
&=&2f(-fg) \hspace{5em}(①を代入)\\
\\
&=&-2f^2g\\
\\
&=&-2gg' \hspace{5em}(②を代入)\\
\\
&=&-(g^2)'\\
\end{eqnarray*}
$tで積分して \quad g'=-g^2+C \ \ (C\ は積分定数) \hspace{5em}③$
$f^2=-g^2+C \hspace{5em}(②を代入)$
$f^2+g^2=C \quad 問題文ではこの \ C\ を \ p(t)\ とおいてあります。$
$初期条件 \quad f(0)=1,\quad g(0)=0 \quad より \ \ C=1 \quad (ですから \ \ p(t)=1 \ \ です)$
$したがって \quad f^2+g^2=1 \quad となります。$
$③式より \quad g'=-g^2+1 \quad だから$
$\cfrac{dg}{dt}=1-g^2$
$これは変数分離形の微分方程式と呼ばれる最も基本的な微分方程式です。$
$\cfrac{dg}{(1+g)(1-g)}=dt$
$\cfrac{1}{2}\big(\cfrac{1}{1+g}+\cfrac{1}{1-g}\big)dg=dt$
$\log(1+g)-\log(1-g)=2t+C \ \ (C\ は積分定数)$
$t=0 \ \ を代入して \ \ g(0)=0 \ \ だから \quad \log1 -\log1=C \quad \therefore\ \ C=0$
$\log(1+g)-\log(1-g)=2t $
$問題文では \ \ 左辺=q(t) \ \ とおいてありますから \quad q(t)=2t \quad となります。$
$ここから \ \ g(t) ,\ \ f(t)\ \ を求めることは上に記述してあります。$
$このように、微分方程式を解く過程で、p(t),\ \ q(t)\ \ が出てきたわけです。$
メインメニュー に戻る