MY MATH NOTE

東京工業大学(理系) 2024年　問題1

$xy\ 平面上の曲線 \ \ y=\dfrac{1}{2}x^2 \ \ に、点(a,\ \dfrac{1}{2}a^2) \ \ (a > 0)\ \ で接する円のうち、y\ 軸の正の部分にも接するものを$
$S_a \ とおく。a\ が正の実数を動くときの \ S_a\ の中心の軌跡を \ C,とくに \ S_1\ の中心を \ P\ とする。$
$(1)\ \ 点P\ の座標を求めよ。$
$(2)\ \ 点P\ における曲線 \ C\ の接線の傾きを求めよ。$

(1)

　
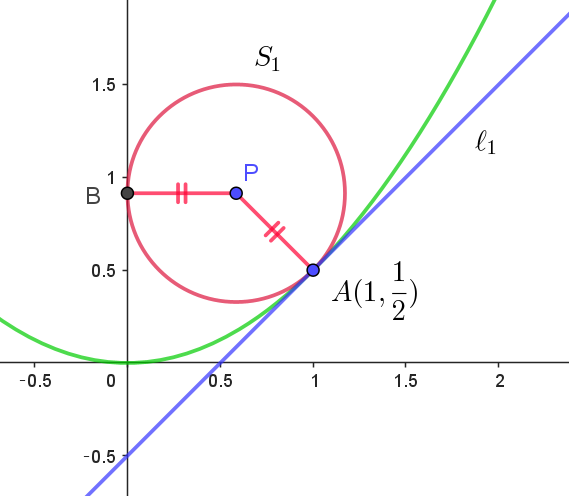
$2\ 曲線が接するとは、交点において共通の接線をもつことである。$

$また、円の接線は中心を通る直線に垂直である。$

$A(1,\ \dfrac{1}{2}) \quad とおく。$

$y=\dfrac{1}{2}x^2 \ \ 上の点A(1,\ \dfrac{1}{2})\ \ における接線の方程式 \ \ \ell_1 \ は$

$y'=x \quad より \quad y=(x-1)+\dfrac{1}{2}=x-\dfrac{1}{2}$

$\ell_1 : x-y-\dfrac{1}{2}=0$

$S_1 \ の中心 \ P\ を \ P(t,\ u)\ \ とおくと \ P\ と \ \ell_1 \ との距離 \ PA\ は$

$PA=\cfrac{|t-u-\dfrac{1}{2}|}{\sqrt{2}}$

$P(t,\ u)\ は接線 \ \ell_1 \ より上にあるから \quad u > t-\dfrac{1}{2}$

$よって \quad PA=\cfrac{u-t + \dfrac{1}{2}}{\sqrt{2}}$

$円 \ S_1\ は \ y\ 軸にも接するから接点を \ B\ とおくと \quad PB=t$

$PA,\ PB \ はともに円 \ S_1 \ の半径だから等しい。$

$よって \quad t=\cfrac{u-t + \dfrac{1}{2}}{\sqrt{2}}$

$\sqrt{2}t=u-t+\cfrac{1}{2}$

$u=(\sqrt{2}+1)t-\cfrac{1}{2} \hspace{5em}①$

$また、PA \perp \ell_1 \quad だから \quad \cfrac{u-\dfrac{1}{2}}{t-1}=-1$

$u=-t+\cfrac{3}{2}　\hspace{7em}②$

$②を①に代入して$

$(\sqrt{2}+1)t-\cfrac{1}{2}=-t+\cfrac{3}{2}$

$(2+\sqrt{2})t=2$

$t=\cfrac{2}{2+\sqrt{2}}=2-\sqrt{2}$

$②に代入して \quad u=-(2-\sqrt{2})+\cfrac{3}{2}=\sqrt{2}-\cfrac{1}{2}$

$よって \quad P(2-\sqrt{2},\ \sqrt{2}-\cfrac{1}{2})$

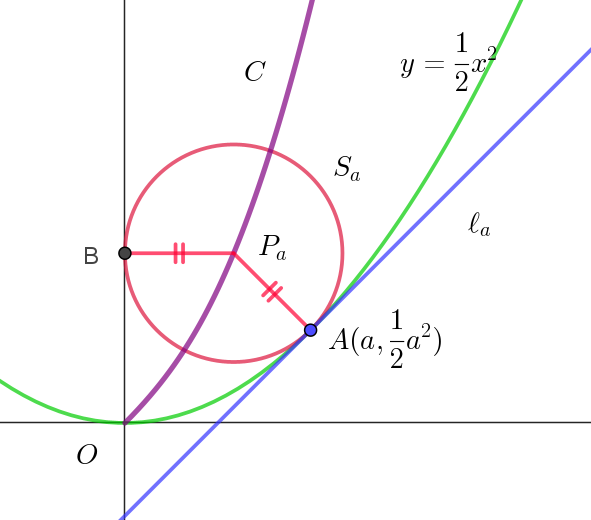
(2)

　
$よって \quad t=\cfrac{u-at + \dfrac{1}{2}a^2}{\sqrt{a^2+1}}$

$t\sqrt{a^2+1}=u-at+\cfrac{1}{2}a^2$

$u=(\sqrt{a^2+1}+a)t-\cfrac{1}{2}a^2 \hspace{5em}③$

$また、P_a A \perp \ell_a \quad だから\quad \cfrac{u-\dfrac{1}{2}a^2}{t-a}=-\cfrac{1}{a}$

$au=-t+\cfrac{1}{2}a^3+a　\hspace{7em}④$

$③を④に代入して$

$a\big\{(\sqrt{a^2+1}+a)t-\cfrac{1}{2}a^2\big\}=-t+\cfrac{1}{2}a^3+a$

$(a\sqrt{a^2+1}+a^2+1)t=a^3+a$

\begin{eqnarray*} t &=&\cfrac{a(a^2+1)}{a\sqrt{a^2+1}+a^2+1} \hspace{5em}(分母・分子を\ \ \sqrt{a^2+1}\ \ で割って)\\ \\ &=&\cfrac{a\sqrt{a^2+1}}{a+ \sqrt{a^2+1}} \\ \end{eqnarray*}
$③に代入して$
\begin{eqnarray*} u &=&(\sqrt{a^2+1}+a) \times \cfrac{a\sqrt{a^2+1}}{a+ \sqrt{a^2+1}} -\cfrac{1}{2}a^2\\ \\ &=&a\sqrt{a^2+1}-\cfrac{1}{2}a^2 \end{eqnarray*}
$u \ を \ t\ の関数とみたときの導関数は$

$\cfrac{du}{da}=\sqrt{a^2+1}+a \times \dfrac{a}{\sqrt{a^2+1}} -a=\sqrt{a^2+1}+ \dfrac{a^2}{\sqrt{a^2+1}} -a$

$t=\cfrac{a\sqrt{a^2+1}}{a+ \sqrt{a^2+1}}=a\sqrt{a^2+1}(\sqrt{a^2+1}-a)=a(a^2+1)-a^2\sqrt{a^2+1} \quad と変形して$

$\cfrac{dt}{da}=3a^2+1-\{2a\sqrt{a^2+1}+a^2 \times \dfrac{a}{\sqrt{a^2+1}}\}=3a^2+1-2a\sqrt{a^2+1}- \dfrac{a^3}{\sqrt{a^2+1}}$

$\cfrac{du}{dt}=\cfrac{\dfrac{du}{da}}{\dfrac{dt}{da}}=\cfrac{\sqrt{a^2+1}+ \dfrac{a^2}{\sqrt{a^2+1}} -a}{3a^2+1-2a\sqrt{a^2+1} - \dfrac{a^3}{\sqrt{a^2+1}}}$

$とくに \ \ a=1 \ のときの微分係数、すなわち\ \ 点P\ における曲線 \ C\ の接線の傾きは$

\begin{eqnarray*} \cfrac{du}{dt} &=&\cfrac{\sqrt{2}+\dfrac{1}{\sqrt{2}}-1}{4-2\sqrt{2}-\dfrac{1}{\sqrt{2}}}\\ \\ &=&\cfrac{2+1-\sqrt{2}}{4\sqrt{2}-4-1}\\ \\ &=&\cfrac{3-\sqrt{2}}{4\sqrt{2}-5}\\ \\ &=&\cfrac{(3-\sqrt{2})(4\sqrt{2}+5)}{32-25}\\ \\ &=&\cfrac{7+7\sqrt{2}}{7}\\ \\ &=&1+\sqrt{2} \end{eqnarray*}

$(補充)$

$t=t(a),\ \ u=u(a)\ \ からパラメータ \ a\ を消去して、u\ を \ t\ の関数として求まれば軌跡 \ C\ の方程式が$

$わかるが、かなり複雑な式になると思われる。$

$設問は、点P\ における曲線 \ C\ の接線の傾きを求めること、すなわち微分係数を求めるだけである。$

$なお、図形描画ソフトを用いてかいた軌跡 \ C\ は上図の紫色の曲線である。$

ページの先頭へ↑