東京工業大学 2018年 問題5
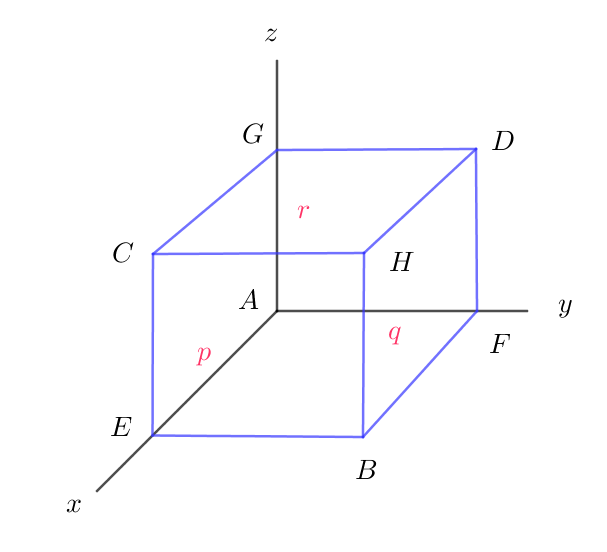
$x\ y\ z\ 空間内の \ 1\ 辺の長さが \ 1\ の立方体 \ \{(x,y,z)\ |\ 0 \leqq x \leqq 1,\ 0 \leqq y \leqq 1,\ 0 \leqq z \leqq 1\ \}を \ Q\ とする。点 \ X\ は$
$頂点 \ A(0,\ 0,\ 0)から出発して \ Q\ の辺上を \ 1\ 秒ごとに長さ \ 1\ だけ進んで隣の頂点に移動する。X \ が \ x\ 軸、$
$y\ 軸、\ z\ 軸に平行に進む確率はそれぞれ \ p,\ q,\ r\ である。ただし、p \geqq 0,\ q \geqq 0,\ r \geqq 0,\ p+q+r=1\ である。$
$X\ が \ n\ 秒後に頂点 \ A(0,\ 0,\ 0),\ B(1,\ 1,\ 0),\ C(\ 1,\ 0,\ 1),\ D(0,\ 1,\ 1)\ にある確率をそれぞれ \ a_n,\ b_n,\ c_n.\ d_n\ とする。$
$(1)\ \ a_{n+2}\ を \ a_n,\ b_n,\ c_n,\ d_n\ と \ p,\ q,\ r\ を用いて表せ。$
$(2)\ \ a_n-b_n+c_n-d_n\ を \ p,\ q,\ r,\ n\ を用いて表せ。$
$(3)\ \ a_n\ を \ p,\ q,\ r,\ n\ を用いて表せ。$
$(解説)$
$(1)\ \ 頂点 \ A\ から頂点A,B,C,Dへの移動には偶数秒かかる。$
$(2)\ \ (1)にならって、b_{n+2},\ c_{n+2},\ d_{n+2}\ を求めておきます。$
$(3)\ \ (2)にならって、b_n,\ c_n,\ d_n\ の符号が異なる漸化式を$
$\quad 求めておきます。$
$\quad もう一つ重要な漸化式を忘れないでください。$
$\quad これら \ 4\ つの式から \ a_n\ が求まります。$
$点 \ A,\ B,\ C,\ D\ から点 \ A,\ B,\ C,\ D\ にそれぞれ進むには$
$必ず偶数時間かかり、奇数時間では到達できないことを$
$押さえておきましょう。$
(1)
$n\ を偶数として、n\ 秒後にいる頂点 \ A,\ B,\ C,\ D\ から \ n+2\ 秒後$
$に頂点 \ A\ に戻るには、右の樹形図のような(ア)~(エ)の \ 4\ 通りの$
$場合がある。$
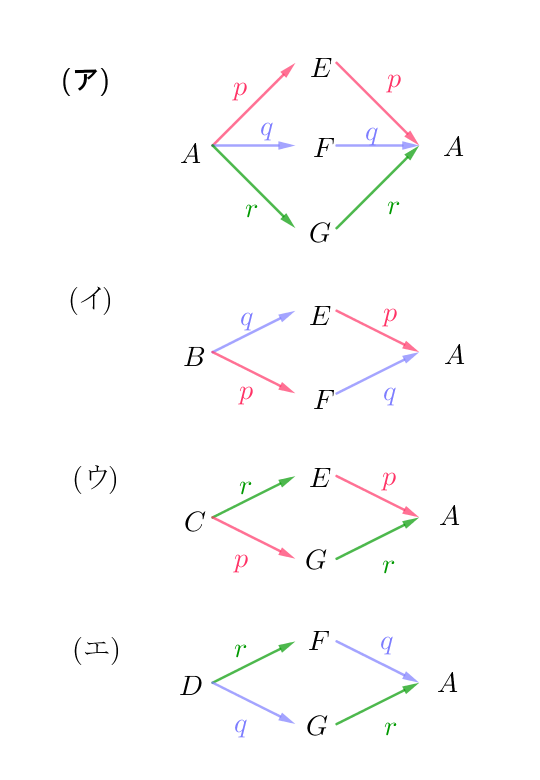
$(ア)の場合 \quad a_{n+2}=(p^2+q^2+r^2)a_n$
$(イ)の場合 \quad a_{n+2}=2pqb_n$
$(ウ)の場合 \quad a_{n+2}=2rpc_n$
$(エ)の場合 \quad a_{n+2}=2qrd_n$
$これらの事象は互いに排反だから$
$\quad a_{n+2}=(p^2+q^2+r^2)a_n+2pqb_n+2qrd_n+2rpc_n$
(2)
$(1)と同様にして$
$\quad b_{n+2}=(p^2+q^2+r^2)b_n+2pqa_n+2qrc_n+2rpd_n$
$\quad c_{n+2}=(p^2+q^2+r^2)c_n+2pqd_n+2qrb_n+2rpa_n$
$\quad d_{n+2}=(p^2+q^2+r^2)d_n+2pqc_n+2qra_n+2rpb_n$
$これらより$
\begin{eqnarray*} & &a_{n+2}-b_{n+2}+c_{n+2}-d_{n+2}\\ \\ &=&(p^2+q^2+r^2)(a_n-b_n+c_n-d_n)-2pq(a_n-b_n+c_n-d_n)-2qr(a_n-b_n+c_n-d_n)+2rp(a_n-b_n+c_n-d_n)\\ \\ &=&(p^2+q^2+r^2-2pq-2qr+2rp)(a_n-b_n+c_n-d_n)\\ \\ &=&(p-q+r)^2(a_n-b_n+c_n-d_n)\\ \end{eqnarray*} $\quad n \ \longrightarrow \ n-2 \quad とおくと$
\begin{eqnarray*} & &a_n-b_n+c_n-d_n\\ \\ &=&(p-q+r)^2(a_{n-2}-b_{n-2}+c_{n-2}-d_{n-2})\\ \\ &=&(p-q+r)^4(a_{n-4}-b_{n-4}+c_{n-4}-d_{n-4})\\ & & \vdots\\ &=&(p-q+r)^n(a_0-b_0+c_0-d_0)\\ \end{eqnarray*}
$\quad a_0=1,\ b_0=0,\ c_0=0,\ d_0=0 \quad だから$
$\qquad a_n-b_n+c_n-d_n=(p-q+r)^n \hspace{5em}①$
$同様にして$
\begin{eqnarray*} & &a_{n+2}+b_{n+2}-c_{n+2}-d_{n+2}\\ \\ &=&(p^2+q^2+r^2+2pq-2qr-2rp)(a_n+b_n-c_n-d_n)\\ \\ &=&(p+q-r)^2(a_n+b_n-c_n-d_n)\\ \end{eqnarray*}
$\qquad a_n+b_n-c_n-d_n=(p+q-r)^n \hspace{5em}②$
$さらに$
\begin{eqnarray*} & &a_{n+2}-b_{n+2}-c_{n+2}+d_{n+2}\\ \\ &=&(p^2+q^2+r^2-2pq+2qr-2rp)(a_n-b_n-c_n+d_n)\\ \\ &=&(-p+q+r)^2(a_n-b_n-c_n+d_n)\\ \end{eqnarray*}
$\qquad a_n-b_n-c_n+d_n=(-p+q+r)^n \hspace{5em}③$
$また、n秒後には点 \ A,\ B,\ C,\ D\ のどれかにいるから、全確率の定理より$
$\qquad a_n+b_n+c_n+d_n=1 \hspace{10em}④$
$①+②+③+④ \quad より$
$\qquad 4a_n=1+(p-q+r)^n+(p+q-r)^n+(p-q-r)^n$
$よって \quad n\ が偶数のとき$
\begin{eqnarray*} a_n &=&\cfrac{1}{4}\{1+(p-q+r)^n+(p+q-r)^n+(-p+q+r)^n\}\\ &=&\cfrac{1}{4}\{1+(1-2q)^n+(1-2r)^n+(1-2p)^n\}\\ \end{eqnarray*}
$ただし、n\ が奇数のときは \ \ a_n=0 \ \ である。$
$(補充)$
$n\ が偶数のとき$
$-①+②-③+④ \quad より \quad b_n=\cfrac{1}{4}\{1-(1-2q)^n+(1-2r)^n-(1-2p)^n\}$
$①-②-③+④ \quad より \quad c_n=\cfrac{1}{4}\{1+(1-2q)^n-(1-2r)^n-(1-2p)^n\}$
$-①-②+③+④ \quad より \quad d_n=\cfrac{1}{4}\{1-(1-2q)^n-(1-2r)^n+(1-2p)^n\}$
メインメニュー に戻る